1. ELEMENTARY MECHANICS

This lecture applies elementary mechanics to an expanding universe. Attention is given to puzzles such as the role of boundary conditions and conservation laws.

1.1. Newtonian dynamics in cosmology

For a finite, self-gravitating set of mass points with positions r_i(t) in an otherwise empty universe, Newton's laws (assuming nonrelativistic motions and no non-gravitational forces) are

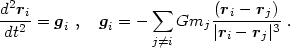(1.1)

In the limit of infinitely many particles each with infinitesimal mass d³r, we can also obtain g_i = g(r_i, t) as the irrotational solution to the Poisson equation,

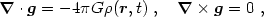(1.2)

which may be written

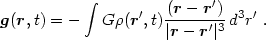(1.3)

The Newtonian potential , defined so that g = - / r (using partial derivatives to indicate the gradient with respect to r), obeys ² = 4 G .

If the mass density is finite and nonzero only in a finite volume, then g (and also ) generally converges to a finite value everywhere, with g 0 as r . If, however, remains finite as r , then diverges and g depends on boundary conditions at infinity.

Consider the dilemma faced by Newton in his correspondence with Bentley concerning the gravitational field in cosmology (Munitz 1957). What is g in an infinite homogeneous medium? If we consider first a bounded sphere of radius R, Gauss' theorem quickly gives us g = - (4 / 3) G r for r < R. This result is unchanged as R , so we might conclude that g is well-defined at any finite r. Suppose, however, that the surface bounding the mass is a spheroid (a flattened or elongated sphere, whose cross-section is an ellipse) of eccentricity e > 0. In this case the gravity field is nonradial (see Binney & Tremaine 1987, Section 2.3, for expressions). The only difference in the mass distribution is in the shell between the spheroid and its circumscribed sphere, yet the gravity field is changed everywhere except at r = 0. An inhomogeneous density field further changes g. Thus, the gravity field in cosmology depends on boundary conditions at infinity.

There is an additional paradox of Newtonian gravity in an infinite homogeneous medium: g = 0 at one point but is nonzero elsewhere (at least in the spherical and spheroidal examples given above), in apparent violation of the Newtonian relativity of absolute space. Newton avoided this problem (incorrectly, in hindsight) by assuming that gravitational forces due to mass at infinity cancel everywhere so that a static solution exists.

These problems are resolved in general relativity (GR), which forces us to complicate the treatment of Newtonian gravity in absolute space. First, in GR distant matter curves spacetime so that (r, t) do not provide good coordinates in cosmology. Second, in GR we must specify a global spacetime geometry explicitly taking into account distant boundary conditions.

What coordinates shall we take in cosmology? First note that a homogeneous self-gravitating mass distribution cannot remain static (unless non-Newtonian physics such as a fine-tuned cosmological constant is added to the model, as was proposed by Einstein in 1917). The observed mass distribution is (on average) expanding on large scales. For a uniform expansion, all separations scale in proportion with a cosmic scale factor a(t). Even though the expansion is not perfectly uniform, it is perfectly reasonable to factor out the mean expansion to account for the dominant motions at large distances as in Figure 1. We do this by defining comoving coordinates x and conformal time as follows:

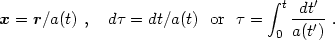(1.4)

The starting time for the expansion is = 0 and t = 0 when a = 0; if this time was nonexistent (or ill-defined in classical terms) then we can set the lower limit of integration for (t) to any convenient value. Although the units of a are arbitrary, I follow the standard convention of Peebles (1980) in setting a = 1 today when t = t₀ and = ₀. A radiation source emitting radiation at < ₀ has redshift / ₀ = z = - 1 + a^-1 where ₀ is the rest wavelength.

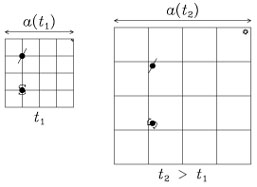Figure 1. Perturbed Hubble expansion.

For a perfectly uniform expansion, the comoving position vectors x remain fixed for all particles. For a perturbed expansion, each particle follows a trajectory x() [or x(t)]. The comoving coordinate velocity, known also as the peculiar velocity, is

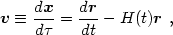(1.5)

where H(t) = d ln a/dt = a^-2da / d is the Hubble parameter. Note that v is the proper velocity measured by a comoving observer at x, i.e., one whose comoving position is fixed.

[The distinction between "proper" and "comoving" quantities is important. Proper quantities are physical observables, and they do not change if the expansion factor is multiplied by a constant. Thus, v = dx / d = (adx) / (adt) is a proper quantity, while dx/dt is not. This is why I prefer rather than t as the independent variable.]

We shall assume that peculiar velocities are of the same order at all distances and in all directions, consistent with the choice of a homogeneous and isotropic mean expansion scale factor. These assumptions are consistent with the Cosmological Principle, which states that the universe is approximately homogeneous and isotropic when averaged over large volumes. In general relativity theory, the Cosmological Principle is applied by assuming that we live in a perturbed Robertson-Walker spacetime. Locally, the GR description is equivalent to Newtonian cosmology plus the boundary conditions that the mass distribution is (to sufficient accuracy) homogeneous and isotropic at infinity.

Unless otherwise stated, in this and the following lectures (until section 4) I shall use 3-vectors for spatial vectors assuming an orthonormal basis. Thus, A ^. B = A_iB_i = Aⁱ B_i = Aⁱ Bⁱ with summation implied from i = 1 to 3. Note that A_i = Aⁱ are Cartesian components, whether comoving or proper, and they are to be regarded (in this Newtonian treatment) as 3-vectors, not the spatial parts of 4-vectors. (If we were to use 4-vectors, then A_i = g_ij A^j = a² Aⁱ in a Robertson-Walker spacetime. Because we are not using 4-vectors, there is no factor of a² distinguishing covariant and contravariant components.) This treatment requires space to be Euclidean, which is believed to be an excellent approximation everywhere except very near relativistic compact objects such as black holes and, possibly, on scales comparable to or larger than the Hubble distance c / H. (In section 4 the restrictions to Cartesian components and Euclidean space will be dropped.) Also, gradients and time derivatives will be taken with respect to the comoving coordinates: / x, ^. / .

Before proceeding further we must derive the laws governing the mean expansion. Consider a spherical uniform mass distribution with mass density and radius r = xa(t) with x = constant. Newtonian energy conservation states

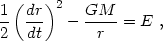implying

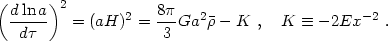(1.6)

This result, known as the Friedmann equation, is valid (from GR) even if includes relativistic particles or vacuum energy density _vac = / (8G) (where is the cosmological constant). The cosmic density parameter is 8 G / (3H²), so the Friedmann equation may also be written K = ( - 1)(aH)². Homogeneous expansion, with a = a() independent of x, requires K = constant in addition to = 0. In GR one finds that K is related to the curvature of space (i.e., of hypersurfaces of constant ). The solutions of eq. (1.6) for zero-pressure (Friedmann) models, two-component models with nonrelativistic matter and radiation, and other simple equations of state may be found in textbooks (e.g., Padmanabhan 1993, Peebles 1993) or derived as good practice for the student.

At last we are ready to describe the motion of a nonuniform medium in Newtonian cosmology with mass density (x, ) = () + (x, ). We start from Newton's law in proper coordinates, d² r / dt² = g, and transform to comoving coordinates and conformal time:

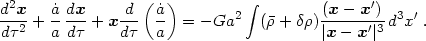We eliminate the homogeneous terms (those present in a homogeneous universe) as follows. First, assuming that the universe is, on average, spherically symmetric at large distance, the first term on the right-hand side becomes (from Gauss' theorem) - (4/3) Ga² x. (This is where the boundary conditions at infinity explicitly are used.) To get the term proportional to x on the left-hand side, differentiate the Friedmann equation: ( / a)d ( / a) / d = (4G/3)d ( a²) / d. For nonrelativistic matter, a^-3, implying d ( a²) / d = - a, so d ( / a) / d = -(4/3) Ga² . (If includes relativistic matter, not only is d / d changed, so is the gravitational field. Our derivation gives essentially the correct final result in this case, but its justification requires GR.) We conclude that the homogeneous terms cancel, so that the equation of motion becomes

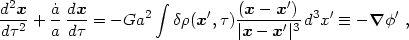where

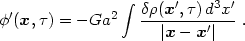Note that ' is a proper quantity: a²d³x' / |x - x' | ~ d³r / |r - r' |.

If d³x 0 when the integral is taken over all space - as happens if the density field approaches homogeneity and isotropy on large scales, with being the volume-averaged density - then ' is finite and well-defined (except, of course, on top of point masses, which we ignore by treating the density field as being continuous). Newton's dilemma is then resolved: we have no ambiguity in the equation of motion for x(). We conclude that ', sometimes called the "peculiar" gravitational potential, is the correct Newtonian potential in cosmology provided we work in comoving coordinates. Therefore we shall drop the prime and the quaint historical adjective "peculiar." In summary, the equations of motion become

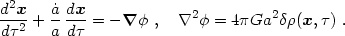(1.7)

As we shall see in section 4, the same equations follow in the weak-field (|| << c²), slow-motion (v² << c²) limit of GR for a perturbed Robertson-Walker spacetime. If Newton had pondered more carefully the role of boundary conditions at infinity, he might have invented modern theoretical cosmology!