4.3.2. Small scale anisotropy

On small angular scales (<< ct₀, the horizon scale at present), the residual radiation temperature fluctuations at present reduce to an approximate expression of the form

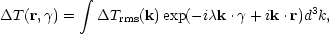(4.19a)

where the amplitude of the Fourier components of the temperature fluctuations,

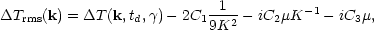(4.19b)

the dimensionless wavenumber K = kt_dc is normalized to the horizon scale at decoupling, µ is the cosine of the angle between wavenumber k and the observation direction and K 3(1 + Z_d)^1/2K = 1 defines a comoving wave vector equal to the present horizon. The first term in T_rms(k) yields the residual temperature fluctuation at the epoch t_d when decoupling is effective, and the remaining terms are associated with secondary fluctuations induced by Thomson scattering in density fluctuations due to the residual ionization remaining after decoupling. The constants C₁ and C₂ are associated with the two adiabatic modes; the C₃ term is due to the isothermal mode; The C₁ term is due to gravitational potential fluctuations [~ (l / ct_d)² / ] and the C₂ term is associated with peculiar motions ~ [(l / ct_d) / ] on the last scattering surface. The former term dominates on large angular scales, where the temperature fluctuations scale as ^(1-n)/2 for / M^-1/2-n/6 (Sachs and Wolfe, 1967).

The angular correlation function for the temperature fluctuations is

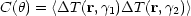(4.20)

where cos = ₁ ^. ₂. This simplifies to

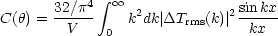(4.21)

where x = |₁ - ₂| for << 1. Comparison with actual observations requires that the correlation function be smeared on small angular scales by convolution with the antenna beam pattern. For example, a Gaussian beam of half-width leads to a smeared correlation function

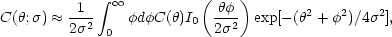(4.22)

where I₀ is a modified Bessel function and << 1 has been assumed. This reduces to C() if = 0. The root mean square temperature fluctuation for an antenna beam that is switched over an angle is

(4.23)

Predicted fluctuations arc shown in Figure 4.3 for a beam with = 3.6' and a recent observational upper limit (T / T 2 × 10^-4 = 3.6' = 9') is also shown. We also show the far infrared experiment with a beam of 5° and an angular resolution of 6°, for which T / T 3 × 10^-5.

The small-scale anisotropy experiment at 6°, while probably an upper limit, is still especially significant. It clearly rules out the n = 1 adiabatic model with = 0.1 (although it is just compatible if = 1). It is also on the verge of constraining an isothermal model with = 1 and n = 0. Experiments on finer angular scales are not as useful. While the 9' experiment also constrains the adiabatic model, it is relatively insensitive to n because of the smearing on the surface of last scattering over angular scales of less than a degree.

The approximate scaling with is such that the predicted values of T / T ^-1, large amplitudes of the initial density fluctuation spectrum being required in a low universe. Adiabatic fluctuations are in conflict on small angular scales with the observational upper limits only if < 0.1. Lowering the upper limit by a factor ~ 4 would permit a test of primordial adiabatic fluctuation spectra with n 3 and isothermal fluctuation spectra with n 0 for cosmological models with 1. This assumes the standard model, in which the intergalactic medium does not become reionized at an epoch z 10, and in which substantial amounts of non-baryonic matter are not present.

In a galaxy formation theory based on adiabatic fluctuations, the first objects capable of ionizing the universe form late, at a redshift 10. Since fluctuations are damped on scales smaller than M_D, the objects must collapse at a relatively late epoch in order to produce the low density large-scale structure of the universe that is observed. Hence reionization probably does not occur if only adiabatic fluctuations are present initially.