4.3. Residual radiation anisotropy

Residual irregularities in the microwave background radiation offer an extremely important test of theories for galaxy, formation. In this section we discuss theoretical predictions for the adiabatic and isothermal perturbations defined in Sections 4.1 and 4.2. The discussion is based on the detailed numerical calculations of Wilson and Silk (1981) and Wilson (1983).

4.3.1. Dipole and quadrupole anisotropy

Consider first the possible anisotropy on very large angular scales. Since we are presumably positioned at random relative to the very large scale structure, the mean dipole moment can be computed, and should give a measure of the observable dipole an isotropy due to very long wavelenghts. The dipole contribution to the temperature fluctuation is P ^. , where the dipole moment

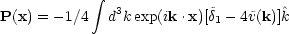(4.14)

Here and in the equations below, 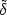₁, 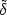₂ etc. refer to the coefficients of the Legendre polynomial expansion of the perturbation to the radiation brightness (Eq. 4.11). The r.m.s. magnitude of the dipole moment, since 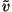is decaying with time as t^-2/3 and 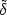₁ t^1/3, is

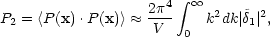(4.15)

where the integration is performed over a suitable large volume V. One can similarly define a quadrupole moment

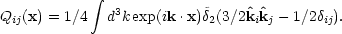(4.16)

The magnitude of the r.m.s. value of the quadrupole moment is given by

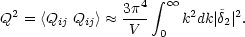(4.17)

The only free parameter in these expressions for P and Q is the spectrum of initial fluctuations. A power-law form |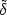|² kⁿ is adopted, and the normalization is determined by evaluating the density fluctuation correlation function and comparing it with the observed galaxy correlation function. The correlation function is defined by

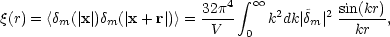(4.18)

and we require it to be unity, at a scale r₀ 4h^-1 Mpc (Peebles, 1979). Alternative normalizations, utilizing an integral over (r) yield similar results.

In Figure 4.3, we present a comparison of observations with the predicted radiation anisotropy for five different models as a function of the initial spectrum. Models 1 and 2 refer to adiabatic fluctuations [(h/0.5)² = 1 and 0.1], and models 3 and 4 refer to isothermal fluctuations [(h / 0.5)² = 1 and 0.1. Consider first the dipole anisotropy. The indicated uncertainties combine both observational effects and theoretical uncertainties in the normalization and spatial averaging (Wilson and Silk, 1981). The observations used allow for the contribution of the Local Supercluster. However, the peak anisotropy, when corrected for galactic rotation, is some 45° away from the Virgo cluster of galaxies, the principal center of the light distribution within the nearest 30 Mpc. Moreover, while the projected component of city towards Virgo is in accord with recent studies of the kinematics Local Supercluster, the orthogonal component appears to be too large to have a local origin. Thus one must resort to a local shearing motion (White and Silk, 1979) or to the existence of a substantial contribution to the dipole anisotropy from fluctuations in density at distances > 30 Mpc. This latter possibility is a natural consequence of the presence of power in the fluctuation spectrum on large scales (see (Clutton-Brock and Peebles, 1981).

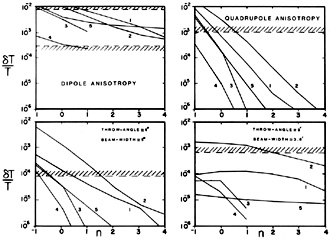Figure 4.3. Predicted temperature fluctuations as a function of the fluctuation spectral index n compared with observational limits. (From Silk and Wilson, 1983). The numbered curves correspond to the following models: (1) adiabatic = 1, h = 0.5; (2) adiabatic = 0.1, h = 0.5; (3) isothermal = 1, h = 0.5; (4) isothermal = 0.1, h = 0.5. Curve (5) shows results for an adiabatic spectrum in a massive neutrino dominated universe, = 0.98, b = 0.02, h = 0.5 (m 20 eV). See Section 9 for further discussion. The quadrupole limit should be reduced by a factor of 10 if we adopt the Fixsen, Cheng and Wilkinson (1983) limit instead of the Fabbri et al. (1980) value (Table 2.1). The dipole upper limit corresponds to a peculiar motion of < 3000 km s-1 when correction is made for Virgo infall: a more realistic limit would reduce this by a factor of three.

These results suggest an alternative explanation for the dipole anisotropy in terms of large scale ( 100 Mpc) fluctuations in the matter distribution. However, at present there is little evidence of such power from studies of the galaxy correlation functions that make use of redshift surveys of galaxies (Davis and Peebles, 1983; Shanks et al. 1983). All models considered here give significant contributions to the dipole anisotropy for essentially any value of n. In particular, the n = 1 spectrum gives excessive dipole anisotropy. Note that n = 0 would be equivalent to zero correlation on a large scale, as would be expected if discrete lumps were laid down at random, and that n = 4 corresponds to the steepest spectrum allowed by non-linear steepening effects and causality arguments (Peebles, 1974b). A spectrum with n - 1 has considerable large-scale power, and may be appropriate for isothermal fluctuations as inferred from N-body simulations of galaxy clustering (see Section 5.3). For the adiabatic model, the Zel'dovich spectrum (n = 1) provides the most desirable initial conditions, since it minimizes the number of free parameters.

Concerning the quadrupole anisotropy, it is apparent that a positive detection would be extremely significant (Sachs and Wolfe, 1967; Peebles, 1981b; Kaiser, 1982; Peebles, 1982a). Suppose that we allow a factor of 3 uncertainty in the normalization, the present upper limits on the dipole and quadrupole (Section 2.5) show that adiabatic models with n 2 are unacceptable. However, a positive detection at the T / T ~ 10^-4 level would agree with the n = 0 isothermal model if 1. This applies to the entropy perturbations described by Eqs. 4.13: these are not zero curvature fluctuations (the curvature fluctuations being of order _m / _r at early epochs). Zero curvature fluctuations yield a far less stringent constraint (Hogan, Kaiser and Rees, 1982). With regard to adiabatic fluctuations, a value n 2 is necessary if = 0.1. An adiabatic fluctuation spectrum flattens, n being reduced by 4, when the fluctuations enter the particle horizon prior to decoupling. Hence the post-decoupling value of the spectral index must exceed -2 for an adiabatic spectrum. A smaller initial value of n, for example the value n = 1, corresponding to constant curvature fluctuations of scale invariant amplitude when entering the particle horizon, yields excessive dipole anisotropy if ~ 1, unless our peculiar motion improbably just cancels the bulk of the cosmological effect. Lowering reduces the peculiar velocities associated with density fluctuations (which scale roughly as ^1/2), and therefore lowers the predicted dipole anisotropy. These results are severely modified in the presence of a cosmological background of massive neutrinos (see Section 9).