4.2. Two Routes to SBH Demographics in Local Quiescent Galaxies
Because of its tightness, the
M
- 
relation provides us
with a direct and powerful
tool to estimate the mass density of SBHs,
, in the local
universe. One approach is
to combine the known mass density of spheroids (e.g.
Fukugita et al. 1998)
with the
mean ratio between the mass of the SBH and that of the host bulge.
Merritt & Ferrarese
(2001a) used the
M
- relation to estimate
M
for a sample of 32
galaxies for which a dynamical measurement of the mass of the hot stellar
component was available (from
Magorrian et al. 1998).
For this sample, the frequency function
N[log(M / Mbulge)] is well
approximated by a Gaussian
with <log(M / Mbulge)> ~ -2.90 and standard
deviation ~ 0.45. This implies
M
/ Mbulge ~ 1.3 × 10-3 or, when
combined with the mass density in local spheroids from
Fukugita et al. (1998),
~ 5 ×
105. This estimate is a factor of five smaller than obtained by
Magorrian et al. (1998)
using what we now
believe to be inflated values for the masses of the central black holes
in many galaxies.
Here I will present an independent derivation of
which, while not
directly leading to
<M
/ Mbulge>, has the advantage of producing an
analytical representation
of the cumulative SBH mass density as a function of
M.
The idea is simple: if
M
correlates with the luminosity of the host bulge, the SBH mass density
can be calculated once the luminosity function of bulges is known. Black
hole masses are related to bulge luminosity directly through the
M
- MB relation, a representation of which is given by
Ferrarese & Merritt
(2000)
as log M
= -0.36MB + 1.2. Unfortunately, the large scatter of
the M
- MB relation
(Fig. 3), combined with the small
number of galaxies on which it is based, makes it
impossible to establish whether elliptical and spiral galaxies follow a
similar relation. Indeed, the observations of
McLure & Dunlop (2001)
cast doubts on whether spirals and lenticulars follow an
M
- MB relation at all. This is
unfortunate since the galaxy luminosity function does show a dependence
on morphology (e.g.,
Marzke et al. 1998),
and it is therefore desirable to
conduct the analysis independently for different Hubble types. An
alternative approach is to derive a relation between
M
and bulge luminosity by combining
the M
- relation (which,
given the present sample, seems independent
of the morphology of the host galaxy) with the Faber-Jackson relation for
ellipticals and its equivalent for spiral bulges. The drawback here is
that the Faber-Jackson relation has large scatter and is ill defined,
especially for bulges.
The luminosity function for spheroids can be derived from the luminosity
function of galaxies, generally represented as a Schechter function,
once a ratio
between total and bulge luminosity (which depends on the Hubble type of
the galaxy considered) is assumed. The latter is adopted from Table 1 of
Fukugita et al. (1998).
Here, I will use the galaxy luminosity function derived by
Marzke et al. (1998)
from the Second Southern Sky Redshift Survey (SSRS2),
corrected to H0 = 75 km s-1
Mpc-1 and an Einstein-de Sitter universe.
Marzke et al. derived luminosity functions separately for E/S0s and
spirals, in a photometric band BSSRS2. This band is
similar to the Johnson's B-band, where representations of both the
M
- MB relation and the Faber-Jackson
relation exist: BSSRS2 = B + 0.26
(Alonso et al. 1993).
A Schechter luminosity function,
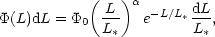
| (3) |
is then easily transformed into a SBH mass density if L = A
Mk,
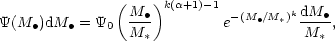
| (4) |
where 
0 =
k
0,
M* =
(
L*100.4 × 0.26 /
A)1/k, and
L/Lbulge = 0.23 for spirals
and 0.76 for E/S0 galaxies.
is the sum
of the ratios between bulge to total
B-band luminosity for different Hubble types, each weighted by
the fraction of the mean luminosity density contributed by each type (from
Fukugita et al. 1998).
Fig. 4 shows the cumulative SBH mass function
separately for the E/S0 and spiral populations, derived from the
M
- MB relation (from
Ferrarese & Merritt 2000,
dotted lines) and the
M
- relation (from this
paper) combined with the
Faber-Jackson relations for ellipticals and spirals (from
Kormendy & Illingworth
1983,
corrected to H0 = 75 km s-1
Mpc-1). While the two distributions differ in the
details, there is little difference in the total mass density, which
falls in the range
(4 - 5) × 105
M
Mpc3. This is in excellent agreement with the estimate of
Merritt & Ferrarese
(2001a).
|
Figure 4. The mass function in local black
holes for spirals (blue), E/S0 (red)
and a complete sample of galaxies (black). Dotted lines are derived
from the
M |
Table 1 summarizes the mass density estimates for SBHs discussed in the preceeding three sections. While a detailed comparison of the distribution of masses remains to be carried out (for instance, Fig. 1 suggests a larger fraction of very massive black holes, M > 109, in high redshift QSOs than have been found in local galaxies), the overall picture is one of agreement: local studies seem to have recovered the overall mass density inferred from high redshift QSOs. It appears that supermassive black holes are a fundamental component of every large galaxy.
| Method | (105
M
Mpc-3)
|
| QSO optical counts, 0.3 < z < 5.0 | 2 - 4 |
| AGN X-ray counts, z > 0.3 | 0.6 - 9 |
| Spectral fit to the X-ray background, z unknown | 2 - 30 |
| Local AGNs, z < 0.1 | 0.05 - 0.6 |
| Local Quiescent Galaxies, z < 0.0003 | 4 - 5 |