3.2. Galalxy formation

Understanding galaxy formation is a much more difficult problem than understanding the evolution of the dark matter distribution. In the CDM theory, galaxies form when gas, initially well mixed with the dark matter, cools and condenses into emerging dark matter halos. In addition to gravity, a non-exhaustive list of the processes that now need to be taken into account includes: the shock heating and cooling of gas into dark halos, the formation of stars from cold gas and the evolution of the resulting stellar population, the feedback processes generated by the ejection of mass and energy from evolving stars, the production and mixing of heavy elements, the extinction and reradiation of stellar light by dust particles, the formation of black holes at the centres of galaxies and the influence of the associated quasar emission. These processes span an enormous range of length and mass scales. For example, the parsec scale relevant to star formation is a factor of 10⁸ smaller than the scale of a galaxy supercluster.

The best that can be done with current computing techniques is to model the evolution of dark matter and gas in a cosmological volume with resolution comparable to a single galaxy. Subgalactic scales must then then be regarded as "subgrid" scales and followed by means of phenomenological models based either on our current physical understanding or on observations. In the approach known as "semi-analytic" modelling (White & Frenk 1991), even the gas dynamics is treated phenomenologically using a simple, spherically symmetric model to describe the accretion and cooling of gas into dark matter halos. It turns out that this simple model works suprisingly well as judged by the good agreement with results of full N-body/gas-dynamical simulations (Benson et al. 2001b, Helly et al. 2002, Yoshida et al. 2002).

The main difficulty encountered in cosmological gas dynamical simulations arises from the need to suppress a cooling instability present in hierarchical clustering models like CDM. The building blocks of galaxies are small clumps that condense at early times. The gas that cools within them has very high density, reflecting the mean density of the Universe at that epoch. Since the cooling rate is proportional to the square of the gas density, in the absence of heat sources, most of the gas would cool in the highest levels of the mass hierarchy leaving no gas to power star formation today or even to provide the hot, X-ray emitting plasma detected in galaxy clusters. Known heat sources are photoionisation by early generations of stars and quasars and the injection of energy from supernovae and active galactic nuclei. These processes, which undoubtedly happened in our Universe, belong to the realm of subgrid physics which cosmological simulations cannot resolve. Different treatments of this "feedback" result in different amounts of cool gas and can lead to very different predictions for the properties of the galaxy population. This is a fundamental problem that afflicts cosmological simulations even when they are complemented by the inclusion of semi-analytic techniques. In this case, the resolution of the calculation can be extended to arbitrarily small mass halos, perhaps allowing a more realistic treatment of feedback. Although they are less general than full gasdynamical simulations, simulations in which the evolution of gas is treated semi-analytically make experimentation with different prescriptions relatively simple and efficient (Kauffmann, White & Guiderdoni 1993, Somerville & Primack 1999, Cole et al. 2000)

Figure 6. A slice 10 h-1 Mpc thick of a simulation of a cubic region of side 141 h-1 Mpc in the CDM cosmology. The grey scale shows a slightly smoothed representation of the dark matter in the N-body simulation. The coloured dots show galaxies; the size of the dots is proportional to the B-band luminosity of the galaxy and the colour represents the B-V colour as given on the scale on the top. The top panel corresponds to redshift z = 0 and the bottom panel to z = 3. (Adapted from Benson et al. 2001a).

The outcome of an N-body dark matter simulation in a CDM universe in which the visible properties of the galaxies have been calculated using the semi-analytic model of Cole et al. (2000) is illustrated in Fig. 6 (Benson et al. 2001a). Galaxies form mostly along the filaments delineated by the dark matter. Red galaxies predominate in the most massive dark matter halos, just as observed in real galaxy clusters. This segregation is a natural outcome of hierarchical clustering from CDM initial conditions. It reflects the fact that the progenitors of rich clusters form substantially earlier than a typical dark matter halo of the same mass. Fig. 7 shows the galaxy luminosity function which describes the abundance of galaxies of different luminosities. The theoretical predictions, shown by the line, agree remarkably well with the observations but this should not be regarded as a spectacular success of the theory because the free parameters in the semi-analytic star formation and feedback model have been tuned to achieve as good a match as possible to this specific observational dataset. In particular, the feedback model has been tuned to produce a relatively flat function at the faint end.

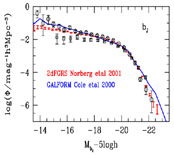Figure 7. The galaxy luminosity function. The symbols show the number of galaxies per unit volume and per unit magnitude measured in various surveys, as a function of galaxy magnitude (open circles: Zucca et al. 1997; open squares: Loveday et al. 1992; thick error bars: Norberg et al. 2001b). The solid line shows the predictions of the semi-analytic model of Cole et al. (2000).

Having fixed the model parameters by reference to a small subset of the data such as the galaxy luminosity function, we can ask whether the same model accounts for other basic observational data. The galaxy autocorrelation function, _gal(r), in the simulations is plotted in Fig. 2 above. On large scales, it follows _dm(r) quite closely, but on small scales it dips below the mass autocorrelation function. This small scale "antibias" has also been seen in N-body/gasdynamical simulations of the CDM cosmology (Pearce et al. 1999, 2001, Dave et al. 1999), and in dark matter simulations that resolve individual galactic halos (Klypin et al. 1999). The galaxy autocorrelation function in the simulations of Benson et al. (2000) agrees remarkably well with the observational data (see also Kauffmann et al. 1999a). This is a genuine success of the theory because no model parameters have been adjusted in this comparison. The differences between the small-scale clustering of galaxies and dark matter result from the interplay between the clustering of dark matter halos and the occupation statistics of galaxies in halos which, in turn, are determined by the physics of galaxy formation. This conclusion, discussed in detail by Benson et al. (2000), has led to the development of an analytic formulation known as the "halo model" (e.g. Seljak 2000, Peacock & Smith 2000, Berlind & Weinberg 2002).

Another genuine prediction of the model is the dependence of the strength of clustering on the luminosity of different subsamples. It can be seen in Fig. 6 that the brightest galaxies are concentrated in the most massive clusters, leading one to suspect that their autocorrelation function must be stronger than average. This is indeed the case, as illustrated in Fig. 8 which compares the variation of the clustering length (defined as the pair separation for which (r) = 1) of galaxy samples of different intrinsic luminosity in the simulations of Benson et al. (2001a) with the observational data obtained from the 2dFGRS by Norberg et al. (2001a). The agreement between theory and observations is remarkable considering that there are no adjustble parameters in this comparison. The reason for the strong clustering of bright galaxies is related to the colour-density relation seen in Fig. 6: the brightest galaxies form in the highest peaks of the density distribution which, in initially Gaussian fields, are more strongly clustered than average peaks which produce less extreme galaxies.

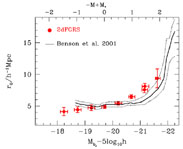Figure 8. The correlation length as a function of the luminosity of different galaxy subsamples. The correlation length is defined as the pair separation for which (r) = 1. The symbols show the results from the 2dFGRS and the line the predictions of the simulations of Benson et al. (2000). (Adapted from Norberg et al. 2001a).

The patch of model universe illustrated in the top panel of Fig. 6 is shown at the earlier epoch corresponding to redshift z = 3 (when the universe was only about 20% of its current age) in the bottom panel of this figure. The galaxies are now blue, reflecting the colour of their younger stellar population. There are fewer galaxies in this plot than in the z = 0 slice. In fact, this is the epoch when the first substantial population of bright galaxies formed in the simulation. As Baugh et al. (1998) argued, the properties of these model galaxies resemble those of the "Lyman-break" galaxies discovered by Steidel et al. (1996), even though different models make somewhat different predictions for their exact properties (Somerville et al. 2001). Most models, however, predict that the brightest galaxies at z = 3 should be strongly clustered (Kauffmann et al. 1999b) and, indeed, the models of Baugh et al. (1998) correctly anticipated that the Lyman-break galaxies would have a clustering length comparable to that of bright galaxies today (Adelberger et al. 1998). This too should be regarded as a significant success of this kind of modelling in the CDM cosmology. As Fig. 6 shows, in contrast to the galaxies, the dark matter is much more weakly clustered at z = 3 than at z = 0, indicating that galaxies were strongly biased at birth.