Annu. Rev. Astron. Astrophys. 1999. 37: 487-531 Copyright © 1999 by Annual Reviews. All rights reserved

2.4. Basics of Abundance Analysis

2.4.1. Collisionally Excited Lines

Collisionally excited lines form by the internal excitation of an ion after electron impact. Their emissivities, that is, the energy released per unit volume and time, follow from the statistical equilibrium of the energy levels. For example, the equilibrium (detailed balance) equation for a 2-level atom is,

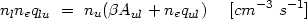(1)

where n_e is the electron density, is the probability for line photons escaping the local region (0 1), A_ul is the spontaneous decay rate, n_u and n_l are the number densities in the upper and lower states, and q_lu and q_ul are the upward and downward collisional-rate coefficients, respectively. Note that ~ ^-1 when >> 1, where is the line-center optical depth (Frisch 1984). For most applications, the ions are mainly in their ground state and n_l is approximately the ionic density. The line emissivity is,

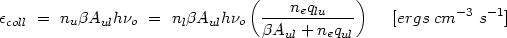(2)

where _o is the line frequency. This emissivity has a strong temperature dependence because q_ul T^-1/2 and (q_lu / q_ul) = (g_u / g_l) exp(-h _o / kT), where g_u and g_l are the statistical weights. In the high-density limit we have,

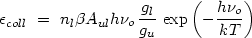(3)

and the levels are said to be thermalized. Line thermalization, where _coll no longer depends on the transition strength, additionally requires >> 1. (A_ul and are both proportional to the oscillator strength, which therefore drops out of the factor A_ul A_ul/ in Equation 3 if >> 1.) At low densities we have,

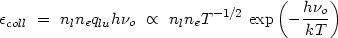(4)

Note that _coll scales here like the density squared, compared with the linear dependence in Equation 3. The critical density, n_crit, between these two limits is the density at which the two terms in the denominator of Equation 2 are equal,

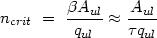(5)

where the approximate relation holds only if >> 1. Physically, n_crit is the density at which the upper level is as likely to be de-excited by collisions as by radiative decay. Note that significant optical depths have the effect of lowering n_crit. Also note that transitions with very different oscillator strengths (but similar collision strengths) will have similar n_crit in the limit >> 1 (because A_ul / is independent of oscillator strength).

2.4.2. Recombination Lines

The most prominent recombination lines belong to HI, HeI, and HeII, with HI Ly being typically strongest. These lines form by the capture of free electrons into excited states, followed by radiative decay to lower states. In the simplest case, in which every photon escapes freely and competing processes are unimportant, the emissivity is,

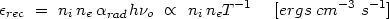(6)

where _rad is the radiative recombination coefficient into the upper energy state and n_i is the number density of parent ions. The temperature dependence is approximate and derives from _rad (see Osterbrock 1989).

2.4.3. Deriving Abundance Ratios

These two types of lines can be combined to form three types of ratios for abundance analysis. The general idea is that, for any element a in ion stage i, the observed line intensity I(a_i) is proportional to the density in that ion, n(a_i), times a function of the overall gas density and temperature F(a_i, T, n), such that I(a_i) = n(a_i)F(a_i, T, n). The ionic abundance ratios are then given by,

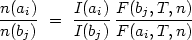(7)

Abundance studies require line pairs for which the ratio of the two functions F is nearly constant or has a limiting behavior that still allow for abundance constraints. The last step is to convert the ionic abundances into elemental abundances, which we express logarithmically relative to solar ratios as ⁽²⁾,

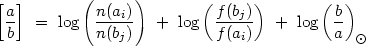(8)

where f(a_i) is the fraction of element a in ion stage i, etc. The middle term on the right-hand side is the ionization correction (IC), which can be deduced from numerical simulations or set to zero (in the log) based on the similarity of the species (Peimbert 1967). Another strategy is to compare summed combinations of lines from different ion stages so that IC tends to zero on average (Davidson 1977).

Ratios of pure recombination lines are simplest because they are least sensitive to the temperature and density. In principle, we could derive the He/H abundance from these ratios. However, in practice, all of the strong HI and HeI recombination lines in QSOs, most notably Ly, are affected by collisions and thermalization effects. Moreover, because H⁰, He⁺ and He⁺² have different ionization energies, they need not be cospatial in the BELR, and their levels of ionization depend on the different numbers of photons available to produce each ion (Williams 1971). As a result, the H and He recombination spectra are most useful as indicators of the shape of the ionizing continuum (e.g. Korista et al. 1997a). We do not expect substantial deviations from solar He/H abundances anyway, based on normal galactic chemical evolution, and the BEL data are grossly consistent with that expectation.

The second possibility involves the ratio of collisional to recombination lines. These ratios have strong temperature dependences (compare Equations 3 and 4 to Equation 6). Nonetheless, they can still be used for abundance work if the temperature sensitivities are quantified by explicit calculations. For example, there is an upper limit on the line ratio NV 1240/HeII 1640 related to the maximum temperature attained in photoionized BELRs. That upper limit sets a firm lower limit on the N/He abundance (Section 2.6.3 below).

The last ratio and the one most often used involves two collisionally excited lines. Roughly a dozen collisionally excited BELs are routinely measured in the UV spectra of quasars, so there is a variety of possibilities. The ideal collisionally excited line pair would have similar excitation energies, so their ratio has a small h _o / kT and thus a small temperature dependence (Equations 3 and 4). Similar values of n_crit and similar ionization energies further minimize the sensitivities to density and BELR structure. Well-chosen ratios that meet these criteria can sometimes provide abundance estimates without recourse to detailed simulations (e.g. Shields 1976; see Section 2.6.1 below).

² Our notation here is based on the usual definition of logarithmic abundances normalized to solar ratios, [a/b] log(a / b) - log(a / b). Back.