Annu. Rev. Astron. Astrophys. 1999. 37: 487-531 Copyright © 1999 by Annual Reviews. All rights reserved

2.5. Photoionization Simulations

A photoionized cloud is essentially a large-scale fluorescence problem. Energy comes into the cloud via continuum radiation, is converted into kinetic energy by the photoejection of electrons, and then leaves the cloud by various emission processes - mainly line radiation. The lines are thus the primary coolants; their total intensity depends on energy conservation and not at all on particular cloud properties.

In general situations, for example dense environments like BELRs, individual line strengths can be governed by a number of competing processes and by feedback related to the cloud structure and energy balance. Detailed calculations are needed to simultaneously consider a complex network of coupled processes. Here we describe some basic results for the line formation and ionization structure in realistic BELR clouds.

2.5.1. Parameters of Photoionization Equilibrium

The fundamental parameters in photoionization simulations are the shape and intensity of the ionizing continuum, and the space density, column density, and chemical composition of the gas. The flux of hydrogen-ionizing photons at the illuminated face of a cloud is,

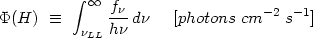(9)

where f is the energy flux density and _LL is the frequency corresponding to 1 Rydberg. A dimensionless ionization parameter U (H) / cn_H is often used instead, where c is the speed of light and n_H is the total hydrogen density (H⁰ + H⁺). U is proportional to the level of ionization and has the advantage of stressing homology relations between clouds with the same U but different (H) and n_H. This simplification is appropriate if we are interested in just the gross ionization structure or in emission lines that are not collisionally suppressed. More generally, we can use either (H) or U as long as the density is also specified.

2.5.2. A Computed Structure

Figure 3 shows the ionization structure of a typical BELR cloud photoionized by a power-law spectrum with = -1.5, where f . The hydrogen recombination front occurs at a depth of ~ 10¹² cm, whereas the He⁺² - He⁺ front is near 10¹¹ cm. Note that there is significant ionization beyond the nominal H⁰ - H⁺ front, owing to penetrating X-rays and Balmer continuum photoionizations out of the n = 2 level in H⁰ (Kwan & Krolick 1981). Some important low-ionization lines like FeII form in that region. The ionization fractions in plots like Figure 3 help us identify ions, such as O⁺⁵, N⁺⁴ and He⁺², that are roughly co-spatial and thus good candidates for abundance comparisons.

Figure 3. Ionization structure for a nominal BELR cloud with nH = 1010 cm-3, log U = -1.5, and solar abundances.

2.5.3. An Example: the CIV 1549 Equivalent Width

CIV 1549 is one of the strongest collisionally excited lines in quasar spectra. The left panel of Figure 4 shows how its predicted equivalent width changes with the density (n_H) and ionizing flux [(H); see Korista et al. 1997b for many more similar plots]. Powerful selection effects are clearly at work; the line radiates efficiently over just a narrow range of parameters. Varying (H) is equivalent to moving the cloud closer or farther from the continuum source. The line is weak at large values of (H) because carbon is too highly ionized, and at low values of (H) because carbon is too neutral. The line strength also changes with the gas density. When the density is above n_crit, the line is collisionally suppressed and other permitted lines take over the cooling. When the density is low, the line weakens as the many forbidden and semiforbidden lines become efficient coolants, and the gas temperature declines. The line is most prominent at n_H 10¹⁰ cm^-3 and log U -1.5, which are the canonical BELR parameters deduced over 20 years ago from analysis of the CIV emission (Davison & Netzer 1979).

Figure 4. Predicted equivalent width (EW) of CIV 1549 as a function of the cloud density, nH, and incident ionizing flux (H). The equivalent width here is dimensionless (line flux / o fo in the continuum) and applies for the hypothetical case of global covering factor unity. Flux ratios for NV 1240/HeII 1640 and NV/CIV are also shown. Other parameters are the same as those in Figure 3.

These selection effects exist whenever we observe an emission line. Baldwin et al. (1995) showed that a typical quasar BEL spectrum might result simply from selection effects operating in BELRs that have simultaneously a wide range of cloud properties (e.g. density and distance from the QSO). Numerical simulations can identify pairs of lines with similar selection behaviors so that their ratios are insensitive to the ranges or specific values of the parameters.

2.5.4. Line Dependence on Continuum Shape

Figure 5 shows a series of calculations with different incident spectral shapes. The actual shape of the ionizing continua in QSOs is a complicated issue, but the UV-to-X-ray slopes are roughly consistent with ~ -1.5, near the center of the range shown (see Laor 1999, Korista et al. 1997a for recent discussions). The results in Figure 5 mainly reflect the conservation of energy in the cloud. Harder spectra (less negative ) provide more heating per photoionization, leading to higher temperatures. The increased heating requires more line cooling via collisionally excited lines like CIV. The ratio of a collisionally excited line to a recombination line, such as CIV / Ly, is proportional to the cooling per recombination or equivalently the heating per photoionization (Davison & Netzer 1979). Such ratios therefore have a strong continuum-shape dependence. The strengths of collisionally excited lines relative to the adjacent continuum (i.e. their equivalent widths) also depend on the spectral slope because of the temperature sensitivity and because the continuum below the lines might be very different from that controlling the ionization. Ratios of collisionally excited lines, such as NV/CIV, can similarly depend on the spectral shape if their ionization or excitation energies are different. In dense BELRs, these simple behaviors can be moderated by other effects. For example, the Ly equivalent width increases with spectral hardening at fixed U (Figure 5) because it has a significant collisional (temperature-sensitive) contribution.

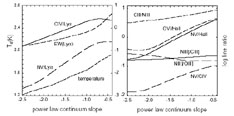Figure 5. Predicted line flux ratios, gas temperatures (T4 = T / 104 K in the O+2 zone, i.e. weighted by the O+2 fraction), and dimensionless equivalent widths in Ly (EW, as in Figure 4) are plotted for clouds photoionized by different power-law spectra. Other parameters are the same as those in Figure 3. The lines are CIII 977, NIII 991, OVI 1034, NV 1240, CIV 1549, HeII 1640, OIII] 1664, NIII] 1750, and CIII] 1909.

2.5.5. Line Dependence on Abundances

The left-hand panel of Figure 6 shows a series of calculations for clouds with different metallicities, Z (scaled from solar and preserving solar ratios among the metals). The strengths of the collisionally excited lines relative to Ly change little with Z. In particular, CIV / Ly varies negligibly for 0.1 Z 30 Z (see also Hamann & Ferland 1993a). We have already noted that these ratios are more sensitive to the continuum shape (Section 2.5.4). Their lack of sensitivity to Z can be traced to feedback in the energy balance. As the metal abundances grow, the line cooling increases. The growing metallicities, which might otherwise increase the metal line strengths, are thus balanced in real clouds by lower temperatures - with the result that the total metal line flux stays constant. This feedback is especially important for strong lines, like CIV, that by themselves control a large fraction of the cooling. Weak lines respond better to abundance changes. At low metallicities (Z 0.02 Z), none of the metal lines are important coolants and their overall strengths do scale with Z.

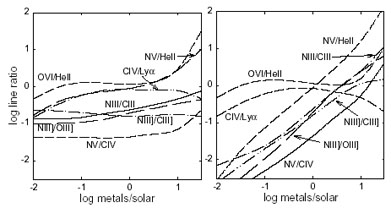Figure 6. Predicted line flux ratios for photoionized clouds with different metallicities Z. All of the metals are scaled together (preserving solar ratios) in the left-hand panel, whereas nitrogen is scaled selectively like Z2 in the right panel. Other parameters are the same as those in Figure 3. See Figure 5 for line notations.

Another factor in the line behaviors at high Z is the increasing bound-free continuum absorption by metal ions. The metals absorb a larger fraction of the far-UV flux at high Z, such that the H and He recombination lines become somewhat weaker. This effect dominates the high-Z rise in OVI/HeII and NV/HeII in Figure 6.

The right-hand panel in Figure 6 shows the same line ratios as before, but in this case nitrogen is scaled such that N/H Z² (where N/H is solar at Z = Z). This selective scaling is based on the expected secondary nucleosynthesis of nitrogen (Section 6 below). Shields (1976) noted that this abundance behavior should occur in QSOs by analogy with its direct observation in galactic HII regions. Figure 6 shows that it leads to a strong metallicity dependence for line ratios involving nitrogen. This strong dependence is possible because the N lines do not control the cooling.