3.1. Closed universe models ( = 1)

Consider a particle moving with negative total energy under the influence of the potential V(a) shown in fig. (2), then the following situations arise (the one dimensional particle coordinate is equivalent to the value of `a' - the expansion factor.)

(i) Oscillating models: The particle moves from left to right (starting from a = 0) but with insufficient energy to surmount the potential barrier. Consequently the expansion factor a(t) first increases then decreases describing a universe which, after expanding, contracts into a singularity. Such models are called oscillating models of the first kind [142].

(ii) Bouncing models: The particle moves from right to left (starting from a = ) again with insufficient energy to surmount the potential, in this case a(t) first decreases then increases and the universe rebounds after collapsing without ever reaching a singular state. Such models are called bouncing models or oscillating models of the second kind, an example of such a model is provided by the complete de Sitter space-time

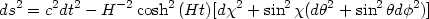
(10)

where - < t < , 0 , 0 , 0 2.

(iii) Static Einstein Universe (SE): The particle is placed at the top of the potential with exactly zero kinetic energy: = = 0. This situation, describes the static Einstein universe. Setting = = 0, = 1 in (3) and assuming for simplicity that matter is pressureless (w = 0) we obtain

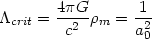
(11)

which relates the value of the cosmological constant to the density of matter and the curvature of space. The volume and mass of a SE universe are respectively V = 2² a₀³, M = V _m = 2² a₀³ _m. As a result M = (c² / 2G)a₀, and one finds lim_a00 M 0, i.e. the mass of the static Einstein universe decreases as its radius shrinks to zero, consequently a static empty universe simply cannot exist ! This feature of SE found favour with the proponents of Mach's principle as discussed in section 2.

(iv) Loitering Universe: The static Einstein universe is clearly unstable: small fluctuations can make it either contract or expand (these correspond to tiny perturbations of a particle located at the hump of V(a) in fig. (2) which cause it to roll either towards the left (a 0) or towards the right (a ). Based on this observation, an interesting new model of the universe was proposed by Eddington and Lemaitre in which the value of was kept slightly larger than _crit. In this case the universe begins from the Big Bang, approaches the static Einstein universe and remains close to it for a substantial period of time before re-expanding [53, 122]. (If < _crit the universe will contract instead of expanding.) The quasi-static or loitering phase, during which the universe remains close to a a₀, has several appealing features not present in models which expand monotonically [169]: (i) density perturbations grow at the exponential (Jeans) rate exp[4 G ]^1/2 t and not at the weaker rate t^2/3 characteristic of an Einstein-de Sitter universe; (ii) a prolonged quasi-static phase results in an older universe, ameliorating the `age' problem which can arise in matter dominated flat cosmologies if the value of the Hubble parameter turns out to be large (see section 4.1).

Interest in loitering models rose dramatically in the late 1960's when observations suggested the existence of an excess of quasars near redshift z_l 2. To explain these observations the Lemaitre model with a quasi-static (loitering) phase at z_l 2 was invoked [160, 175, 166]. (Loitering at z_l arises if the cosmological constant exactly balances _m leading to the relation: (1 + z_l)³ = / _m, where = / 3H². A decaying cosmological constant will lead to loitering at higher values of z_l which has certain advantages from the standpoint of current observations [169].)

(v) Monotonic Universe: The particle approaches the potential from the left (a = 0) with sufficient energy to surmount it and travel on towards a . In such a situation the scale factor will have an inflection point at 0, > 0. By adjusting initial conditions so that the particle remains close to the hump of the potential for a sufficiently long duration, one recovers the `loitering' models discussed in (iv).

(vi) Nonsingular Oscillating model: Another cosmological model deserving mention consists of a form of matter which behaves as a -term when the universe is small, as the universe expands the -term decays into either radiation or matter. The energy density in such a model can be phenomenologically described by 8 G = / (1 + a^p / ), so that lim_a0 8 G , lim_a 8 G / a^p, p = 3, 4 for matter and radiation respectively. The potential V(a) = - 4 G / 3 a² associated with this model has a broad minimum which leads to a non-singular oscillatory motion of the expansion factor a(t). This toy model is interesting since it exhibits an infinite number of expansion and contraction cycles without ever becoming singular.

(vii) Other possibilities not shown in Figure (1) include `asymptotic models' in which the universe asymptotically approaches or moves away from the static Einstein universe. The reader is referred to [62, 142] for a more quantitative discussion of these issues.

Figure 1. Four distinct possible solutions of the Einstein equations with a cosmological constant are schematically shown for a closed universe ( = + 1). (Incidentally none of these solutions arise if = 0, - 1.)

Although the above discussion referred to cosmological models filled with matter having non-negative pressure and a cosmological constant, it is easy to show that the qualitative behaviour of the universe described in (i) - (vii) remains valid, if we generalize the definition of the -term to include any form of matter which violates the strong energy condition so that + 3P < 0 [169].

Figure 2. The `effective potential' V(a) describing the expansion of the universe in the presence of matter and a cosmological constant (see equation (7)). The large variety of solutions to the Einstein equations can be analyzed by studying the kindered problem of the motion of a particle moving under the influence of the potential V.