3.2. Spatially open and flat cosmological models
The preceding discussion referred to closed universe models for which
= 1 and E < 0.
For flat and open models
( = 0, - 1) the total
energy is non-negative
E 
0 and motion in
the potential V(a) becomes unbounded, since a
particle always has sufficient energy to surmount the potential barrier
in figure (2).
As a result the expansion factor a(t) shows monotonic
behaviour, starting from the singular point at
a = 0, t = 0 and increasing without bound
as t 
.
For 
> 0 the
universe passes through an inflection point
at which the expansion of the universe changes from deceleration
(
< 0)
to acceleration
( > 0) (from (3)
& (4) it can be shown that this usually occurs at a redshift when
is still not
dominating the expansion dynamics of the universe; see
section 4.3).
In the important case when the universe is spatially flat and contains pressureless matter (dust) and a positive cosmological constant, the expansion factor has the exact analytical form:
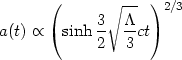
| (12) |
which interpolates smoothly between the matter dominated epoch in the past
(a 
t2/3) and an inflationary epoch in the future
(a
e(/3)1/2t). Equation (12)
will be used later, when we examine some observational aspects of a
universe with a cosmological constant in
Section 4.
Finally, oscillating, bouncing and loitering models, as well as the static Einstein universe, are clearly absent in flat and open FRW models.