


7.2. Vacuum polarization and the value of

Zeldovich (1968), having demonstrated that the energy density of the vacuum was infinite at the one-loop level, suggested that after the removal of divergences, the `regularized' vacuum polarization contributed by a fundamental particle of mass m would be described by the expression
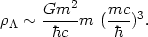
| (81) |
One can arrive at this result by means of the
following argument: the vacuum consists of virtual particle-antiparticle
pairs of mass m and separation
 =
=
 /mc. Although the
regularized self-energy of these pairs is zero, their gravitational
interaction is finite and results in the vacuum energy density
/mc. Although the
regularized self-energy of these pairs is zero, their gravitational
interaction is finite and results in the vacuum energy density
 vac
vac

 vac
c2 ~ (G m2 /
vac
c2 ~ (G m2 /
 ) /
) /
 3 =
Gm6 c4 /
3 =
Gm6 c4 /
 4 corresponding
to (81).
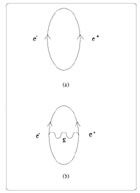
(In terms of Feynman diagrams this corresponds to the energy associated
with the two-loop vacuum graph shown in figure 13.)
Substituting m
4 corresponding
to (81).
(In terms of Feynman diagrams this corresponds to the energy associated
with the two-loop vacuum graph shown in figure 13.)
Substituting m
 me(mp) we find that the electron
(proton) mass gives too small (large) a value for
me(mp) we find that the electron
(proton) mass gives too small (large) a value for

 .
On the other hand, the pion mass gives just the right value
[106]
(13)
.
On the other hand, the pion mass gives just the right value
[106]
(13)
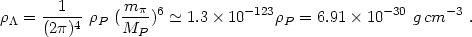
| (83) |
Finally, a small value of
 can
be derived from dimensionless fundamental constants
of nature using purely numerological arguments.
For instance, the fine structure constant
can
be derived from dimensionless fundamental constants
of nature using purely numerological arguments.
For instance, the fine structure constant

 e2 /
e2 /
 c
c
 1/137
when combined with the Planck scale
1/137
when combined with the Planck scale
 P,
suggests the relation
[187]
P,
suggests the relation
[187]
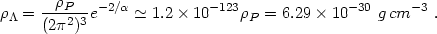
| (84) |
Or, when expressed in terms of

 =
(8
=
(8 G
G

 / 3 H02)
we get
/ 3 H02)
we get 
 h2 = 0.335,
in excellent agreement with observations.
In principle,
h2 = 0.335,
in excellent agreement with observations.
In principle,  could be
some other fundamental constant, such as the
`string constant' associated with superstring theory, which might enter
into exponentially small expressions for
could be
some other fundamental constant, such as the
`string constant' associated with superstring theory, which might enter
into exponentially small expressions for
 of this type.
of this type.
|
Figure 13. This figure shows the one-loop (a) and two-loop (b) vacuum diagrams which contribute towards the vacuum energy density discussed in sections 5 & 7.2 respectively. |
13
The large difference between

 obtained using
(81) for the proton and its observed value prompted Zeldovich to suggest that
Fermi's weak interaction constant GF might play a role in determining the vacuum energy, so that
obtained using
(81) for the proton and its observed value prompted Zeldovich to suggest that
Fermi's weak interaction constant GF might play a role in determining the vacuum energy, so that
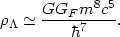
| (82) |
Although this leads to some improvement,

 for the proton is still several
orders of magnnitude larger than its observed value.
Back.
for the proton is still several
orders of magnnitude larger than its observed value.
Back.