Vacuum fluctuations contributing to
generate a
very large (formally infinite) value of the cosmological constant
<T00>vac
0
[k2 + m2]1/2
k2dk. The integral
diverges as k4 resulting in an infinite value
for <T00>vac and hence also
for the cosmological constant
=
8
G
<T00>vac. Since each form of energy
gravitates and therefore reacts back on the space-time geometry, an infinite
value of is
expected to generate an infinitely large space-time
curvature through the semi-classical Einstein equations
G00 = 8G
/ c4 <T00>vac.
One way to avoid this is to assume that the
Planck scale provides a natural ultra-violet cutoff to all field theoretic
processes, this results in
<T00>vac
c5 /
G2
~~
1076GeV4 which is 123 orders of magnitude larger than
the currently observed value
10-47GeV4.
A cutoff at the much lower QCD scale doesn't fare much better since
it generates a cosmological constant
QCD4 ~ 10-3GeV4 -
forty orders of magnitude larger than observed. Clearly the answer
to the cosmological constant issue must lie elsewhere.
The discovery of supersymmetry in the 1970's led to the hope that the cosmological constant problem may be resolved by a judicious balance between bosons and fermions in nature, since bosons and fermions (of identical mass) contribute equally but with opposite sign to the vacuum expectation value of physical quantities, so that
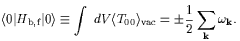
| (1) |
However supersymmetry (if it exists) is broken at the low temperatures
prevailing in the universe today and on this account one should
expect the cosmological
constant to vanish in the early universe, but to reappear during late
times when the temperature has dropped below TSUSY.
This is clearly an undesirable scenario and almost the very opposite
of what one is looking for, since, a large value of
at an
early time is useful from the viewpoint of inflation, whereas a very
small current value of
is in
agreement with observations.
|
Figure 1. The potential describing spontaneous symmetry breaking has the form of a Mexican top hat. The dashed line shows the potential before the cosmological constant has been `renormalized' and the solid line after. |
The cosmological constant also makes an important appearance in models with spontaneous symmetry breaking [17]. For simplicity consider the Lagrangian
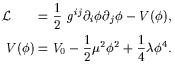
| (2) |
The symmetric state at
= 0 is unstable and the system
settles in the ground state
=
+
or =
-, where
=
[µ2 /
]1/2, thus
breaking the reflection symmetry
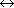- present in the Lagrangian.
If V0 = 0 then this potential results in a broken
symmetry state with a large negative cosmological constant
eff =
V( =
) = -
µ4 /
4. In order to avoid this
situation the value of the free parameter V0 is chosen
to counterbalance
eff, as
a result one sets V0 ~ µ4 /
4 so that
eff /
8G =
V0 - µ4 /
4
10-47GeV
4.
The ensuing `regularization' of the large negative cosmological
constant must be done with considerable care, since even small
`fluctuations' in the final value of
can result in
grave consequences for cosmology. For instance if
eff /
8G < -
10-43GeV 4 the large
attractive force exerted by a negative cosmological constant will
ensure that the universe re-collapses before it reaches `maturity'.
The age of the universe in this case will be <
1 billion years, much too short for galaxies to form and for life
(as we know it) to emerge within the standard big bang scenario.
On the other hand if
eff /
8G >
10-43GeV4, the large
repulsive force generated by
will ensure
that the universe begins accelerating
before gravitationally bound systems have a chance to form.
Such a scenario will also clearly preclude the emergence of life.
The rather small window permitted
for life to emerge in the presence of
has led several researchers
[18,
19,
20]
to develop anthropic arguments for the existence of
a small cosmological constant.
A possibility which is summarised by the following sentence:
"if our big bang is just one of many big bangs, with a wide range of
vacuum energies, then it is natural that some of these big bangs should have
a vacuum energy in the narrow range where galaxies can form, and of
course it is just these big bangs in which there could be astronomers and
physicists wondering about the vacuum energy"
[20].
Anthropic arguments for
will not be examined further by me in this talk.
In the absence of a fundamental symmetry of nature which will set the
value of to
zero one has to look towards physical mechanisms
which might generate an acceptably small value of the
-term today.
Exploring the connection between
quantum fluctuations
and
Zel'dovich suggested that, after the removal of divergences,
the energy density of a virtual particle-antiparticle pair interacting
gravitationally would be
[7]
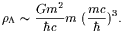
| (3) |
(This result is easy to derive if one notes that the interaction energy
density is typically
vac
vac
c2 ~
(Gm2 /
) /
3 where
=
/
mc is the mean
separation between particle and antiparticle.) This possibility has not
been explored much, perhaps because the proton-antiproton
(electron-positron) contribution gives a very large (small) value for
.
Interestingly the pion-antipion mass gives just the right value
= 1 / (2 )4
Pl
(m /
MPl)6
1.3 ×
10-123
Pl
= 6.91 × 10-30 g cm-3 .
Purely numerological considerations also allow
one to generate a sufficiently small
value of
through a suitable combination of fundamental constants.
For instance the fine structre constant
can be
combined with the Planck density
Pl
to give
[21]
= PL /
(2 2)3
e-2/
1.2 ×
10-123
Pl =
6.29 × 10-30 g cm-3.
A small vacuum energy may be connected to fundamental physics in
other (equally speculative) ways. It is interesting that the mass scale
associated with the scale of supersymmetry breaking
in some models, MSUSY ~ 1 TeV,
lies midway between the Planck scale and 10-3 eV.
The small observed value of the cosmological constant
(10-3eV)4
might therefore be associated with the vacuum in a theory which had a
fundamental mass scale
MX
MSUSY2 / MPl, such that
vac
~ MX4 ~ (10-3eV)4.