3. A DYNAMICAL LAMBDA-TERM

Any fundamental theory of nature which intends to succesfully generate will be confronted by the `fine tuning problem' since the currently observed value of the cosmological constant is miniscule when compared with either the Plan enormous fine tuning of initial conditions is required in order to ensure that the cosmological -term comes to dominate the expansion dynamics of the universe at precisely the current epoch, no sooner and no later.

The fine-tuning problem is rendered less acute if we relax the condition = constant, and (taking the cue from Inflation) try to construct dynamical models for .

Phenomenological approaches to a dynamical -term belong to three main categories [21]:

(1) Kinematic models.

is simply assumed to be a function of either the cosmic time t or the scale factor a(t) of the FRW cosmological model.

(2) Hydrodynamic models.

is described by a barotropic fluid with some equation of state p () (dissipative terms may also be present).

(3) Field-theoretic models. The -term is assumed to be a new physical classical field with some phenomenological Lagrangian.

The simplest class of kinematic models

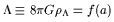
(4)

is equivalent to hydrodynamic models based on an ideal fluid with an equation of state

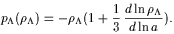
(5)

The expansion of the universe passes through an inflection point the moment it stops decelerating and begins to accelerate. If the equation of state is held constant (w = P / < - 1/3) then the cosmological redshift when this occurs is given by

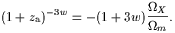
(6)

We find that z_a 0.7 for the cosmological constant (w = - 1) with 0.7 and _m 0.3. The acceleration of the universe is therefore a very recent phenomena. This fact is related to the cosmic coincidence conundrum since it appears that we live during a special era when the density of dark matter and dark energy are comparable. The cosmic coincidence puzzle remains in place even if we relax the assumption w = - 1 and allow dark energy to be time dependent. Indeed, it is easy to show that the equality between dark matter and dark energy takes place at (1 + z_eq)³ = ( / _m)^-1/w. For a cosmological constant this gives z_eq 0.3 and z_a > z_eq implying that the universe begins to accelerate even before it becomes -dominated. For w = - 2/3 z_a = z_eq 0.5, while for stiffer equations of state z_a < z_eq (w > - 2/3) further exacerbating the cosmological coincidence puzzle.