3.1. Scalar field models of dark energy

Although the cosmic coincidence issue remains unresolved, the fine tuning problem facing dark energy/quintessence models with a constant equation of state can be significantly alleviated if we assume that the equation of state is time dependent. An important class of models having this property are scalar fields which couple minimally to gravity and whose energy momentum tensor is

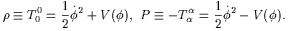
(7)

A scalar field rolling down its potential slowly generates a time-dependent -term since P - - V() if ² << V(). Potentials which satisfy V"V / (V')² 1 have the interesting property that scalar fields approach a common evolutionary path from a wide range of initial conditions [22]. In these so-called `tracker' models the scalar field density (and its equation of state) remains close to that of the dominant background matter during most of cosmological evolution. A good example is provided by the exponential potential V() = V₀ exp[-(8 )^1/2 / M_Pl] [23, 24] for which

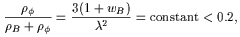
(8)

_B is the background energy density while w_B is the associated equation of state. The lower limit / _total < 0.2 arises because of nucleosynthesis constraints which prevent the energy density in quintessence from being large initially (at t ~ few sec.). Since the ratio / _total remains fixed, exponential potentials on their own cannot supply us with a means of generating dark energy/quintessence at the present epoch. However a suitable modification of the exponential achieves this. For instance the class of potentials [26]

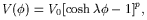
(9)

has the property that w w_B at early times whereas <w> = (p - 1) / (p + 1) at late times. Consequently (9) describes quintessence for p 1/2 and pressureless `cold' dark matter (CDM) for p = 1.

A second example of a tracker-potential is provided by V() = V₀ / [23]. During tracking the ratio of the energy density of the scalar field (quintessence) to that of radiation/matter gradually increases / _B t^{4/(2 + )} while its equation of state remains marginally smaller than the background value w = ( w_B - 2) / ( + 2). These properties allow the scalar field to eventually dominate the density of the universe, giving rise to a late-time epoch of accelerated expansion. (Current observations place the strong constrain 2.)

Several of the quintessential potentials listed in table 1 have been inspired by field theoretic ideas including supersymmetric gauge theories and supergravity, pseudo-goldstone boson models, etc. However accelerated expansion can also arise in models with: (i) topological defects such as a frustrated network of cosmic strings (w - 1/3) and domain walls (w - 2/3) [31]; (ii) scalar field lagrangians with non-linear kinetic terms and no potential term (k-essence [32]); (iii) vacuum polarization associated with an ultra-light scalar field [33, 34]; (iv) non-minimally coupled scalar fields [35]; (v) fields that couple to matter [36]; (vi) scalar-tensor theories of gravity [37]; (vii) brane-world models [38, 39, 40, 41, 43, 44] etc.

Table 1.

Quintessence Potential	Reference
V0 exp(- )	Ratra & Peebles (1988), Wetterich (1988),
	Ferreira & Joyce (1998)
m2 2, 4	Frieman et al (1995)
V0/, > 0	Ratra & Peebles (1988)
V0exp( 2) / , > 0	Brax & Martin (1999,2000)
V0(cosh - 1)p,	Sahni & Wang (2000)
V0sinh- ( ),	Sahni & Starobinsky (2000), Ureña-López & Matos (2000)
V0(e + e )	Barreiro, Copeland & Nunes (2000)
V0(expMp / - 1),	Zlatev, Wang & Steinhardt (1999)
V0[( - B) + A]e- ,	Albrecht & Skordis (2000)

Scalar field based quintessence models can be broadly divided into two classes: (i) those for which / M_Pl << 1 as t t₀, (ii) those for which / M_Pl 1 as t t₀ (t₀ is the present time). An important issue concerning the second class of models is whether quantum corrections become important when / M_Pl 1 and their possible effect on the quintessence potential [45]. One can also ask whether a given choice of parameter values is `natural'. Consider for instance the potential V = M^{4 +} / , current observations indicate V₀ 10^-47GeV⁴ and 2, which together suggest M 0.1 GeV (smaller values of M arise for smaller ) it is not clear whether such small parameter values can be motivated by current models of high energy physics.

Finally, it would be enormously interesting if one and the same field could give rise to both Inflation and dark energy. Such models have been discussed both in the context of standard inflation [46] and brane-world inflation [39, 40, 41], we briefly discuss the second possibility below.