5.3.4. Heating by galaxy motions

Although ongoing heating of the intracluster gas may not be necessary to account for the observed gas temperatures, the estimates given above and the history of the gas are sufficiently uncertain that one cannot rule out ongoing heating as an important processes. One way in which intracluster gas could be heated would be through friction between the gas and the galaxies that are constantly moving throughout the cluster (Ruderman and Spiegel, 1971; Hunt, 1971; Yahil and Ostriker, 1973; Schipper, 1974; Livio et al., 1978; Rephaeli and Salpeter, 1980). The calculation of the magnitude of this drag force and of the consequent heating of the intracluster gas is complicated by the following problems. First, the motion of an average cluster galaxy through the intracluster medium is likely to be just transonic m 1, where m v/c_s is the Mach number, v is the galaxy velocity, and c_s = 1480(T_g / 10⁸ K)^1/2 km/s is the sound speed in the gas. If equation (4.10) for the observed gas temperatures is assumed, and the average galaxy velocity is taken to be 3^1/2 _r, then the average Mach number is <M> 1.5. Thus the galaxy motion cannot be treated as being either highly supersonic (strong shocks, etc.) or very subsonic (incompressible, etc.). In some cases shocks will be formed by the motion, and in some cases no shocks form. Second, the mean free path _i of ions in the intracluster medium due to Coulomb collisions (equation 5.34) is similar to the radius of a galaxy R_gal 20 kpc (Nulsen, 1982). Thus it is unclear whether the intracluster gas should be treated as a collisionless gas or as a fluid, and the role of transport processes such as viscosity (Section 5.4.4) is uncertain. For example, the Reynolds number of the flow about an object of radius r is Re 3(R / _i)m (equation 5.46 below), and thus is somewhat larger than unity if r = R_gal. It is therefore uncertain whether the flow will be laminar or turbulent. The magnetic field can affect transport processes (Section 5.4.3), but the coherence length of the field l_B estimated from Faraday rotation observations is also comparable to the size of a galaxy (Section 3.6). Finally, the nature of the drag force depends on whether the galaxy contains interstellar gas or not. If the galaxy contains no gas, it affects the intracluster medium only through its gravitational field. If the galaxy contains high density gas, it can give the galaxy an effective surface. For example, a gasless galaxy in supersonic motion probably will not produce a bow shock, while a gas-filled galaxy may (Ruderman and Spiegel, 1971; Hunt, 1971; Gisler, 1976).

It is convenient to write the rate of energy loss by the galaxy and the heating rate of the intracluster medium as

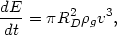
(5.28)

where _g is the intracluster gas density and R_D is the effective radius of the galaxy for producing the drag force. First, assume that the intracluster gas is collisionless. Then the drag is given by the dynamical friction force of equation (2.34) and

(5.29)

where R_A 2Gm/v² is the accretion radius (Ruderman and Spiegel, 1971), m is the galaxy mass, is given by equation (2.29), and x (5/6)^1/2 M. By the virial theorem applied to the galaxy, R_A R_gal(_* / _r)², and the accretion radius is typically much smaller than the galaxy radius, since the galaxy velocity dispersion is smaller than that of a cluster. In the limit of hypersonic motion M >> 1, the term in brackets reduces to unity. In this limit, Rephaeli and Salpeter (1980) have shown that equation (5.29) gives the drag force for any value of the mean free path or viscosity if no gas is present in the galaxy. The definition of must be slightly modified (Ruderman and Speigel, 1971).

For a 10¹¹ M galaxy moving at 1000 km/s through intracluster gas with a proton number density of 10^-3 cm^-3, the rate of heating of the gas is 10⁴¹ erg/s. If the cluster contained 1000 such galaxies, the total heating rate would be 10⁴⁴ erg/s. While not trivial, this heating rate is too small to heat the intracluster gas in a Hubble time (Schipper, 1974; Rephaeli and Salpeter, 1980). If the total mass of intracluster gas is 10¹⁴ M and the gas temperature is 6 × 10⁷ K, then the time required to heat the gas at this rate would be 7 × 10¹¹ yr.

The drag force can be considerably increased if the galaxy contains gas or magnetic fields that prevent the penetration of the galaxy by the intracluster gas (Ruderman and Spiegel, 1971; Yahil and Ostriker, 1973; Livio et al., 1978; Shaviv and Salpeter, 1982; Gaetz et al., 1987). However, the main effect of the drag force may be to remove the gas from the galaxy and heat it to the temperature determined by the galaxy kinetic energy per mass (Section 5.3.3). The stripping of gas from a galaxy is shown in Section 5.9 to be very efficient, and as discussed in Sections 2.10.2 and 4.6, galaxies in X-ray clusters are known to be very deficient in gas. It is possible that galaxies may retain a core of gas produced by stellar mass loss within the galaxy. Gaetz et al. (1987) give useful analytic fitting formulas for drag coefficients for galaxies with stellar mass loss, based on two-dimensional hydrodynamic simulations. Yahil and Ostriker (1973) and Livio et al. (1978) have suggested very large heating rates produced by having high rates of gas output in galaxies. Livio et al. assume a rather large cross section for galaxies and a rather low intracluster gas density. Both of these papers argue that the heating rate due to galaxy motions is so large that the intracluster gas is heated beyond the escape temperature from the cluster, and a cluster wind results (see Section 5.6).

There is a simple argument against the great importance of heating due to drag forces from the motions of galaxies. The mass associated with intracluster gas in a typical X-ray cluster is comparable to or greater than the mass associated with galaxies (Section 4.4.1). The average thermal velocities in the gas are comparable to or greater than the typical galaxy velocities (Sections 4.6, 5.3.2, and 5.5). Thus the total thermal energy in the gas is greater than or comparable to the total kinetic energy in the galaxies. It is difficult to believe that the galaxies heated the gas under these circumstances. If they did, then the massive galaxies would have lost most of their initial kinetic energy in the process; this should have produced quite extreme mass segregation, which is not observed (Section 2.7).