


2.7. Orthogonal series estimators
Orthogonal series estimators approach the density estimation problem from quite a different point of view. They are best explained by a specific example. Suppose that we are trying to estimate a density f on the unit interval [0, 1]. The idea of the orthogonal series method is then to estimate f by estimating the coefficients of its Fourier expansion.
Define the sequence

 (x) by
(x) by
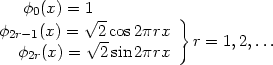
|
Then, by standard mathematical analysis, f can be represented as the
Fourier series

 =0
=0 f
f

 , where, for
each
, where, for
each 
 0,
0,
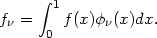
| (2.6) |
For a discussion of the sense in which f is represented by the series, see, for example, Kreider et al. (1966).
Suppose X is a random variable with density f. Then (2.6) can be written
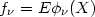
|
and hence a natural, and unbiased, estimator of
f based on a
sample X1,..., Xn from f is
based on a
sample X1,..., Xn from f is
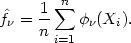
|
Unfortunately, the sum

 =0
=0



 will not be a good estimate of f, but
will `converge' to a sum of delta functions at the observations; to
see this, let
will not be a good estimate of f, but
will `converge' to a sum of delta functions at the observations; to
see this, let
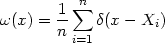
| (2.7) |
where  is the Dirac
delta function. Then, for each
is the Dirac
delta function. Then, for each  ,
,
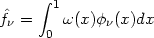
|
and so the

 are exactly the Fourier
coefficients of the function
are exactly the Fourier
coefficients of the function
 .
.
In order to obtain a useful estimate of the density f, it is
necessary to smooth  by
applying a low-pass filter to the sequence of coefficients
by
applying a low-pass filter to the sequence of coefficients

 . The easiest way to do this
is to truncate the expansion
. The easiest way to do this
is to truncate the expansion




 at some point. Choose an
integer K and define the density estimate
at some point. Choose an
integer K and define the density estimate
 by
by
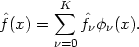
| (2.8) |
The choice of the cutoff point K determines the amount of smoothing.
A more general approach is to taper the series by a sequence of
weights 
 , which satisfy
, which satisfy


 0 as
0 as


 , to obtain the estimate
, to obtain the estimate
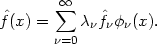
|
The rate at which the weights

 converge to zero will
determine the amount of smoothing.
converge to zero will
determine the amount of smoothing.
Other orthogonal series estimates, no longer necessarily confined to
data lying on a finite interval, can be obtained by using different
orthonormal sequences of functions. Suppose a(x) is a
weighting function and
(
 ) is a series satisfying, for
µ and
) is a series satisfying, for
µ and

 0,
0,
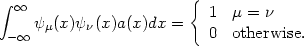
|
For instance, for data resealed to have zero mean and unit variance,
a(x) might be the function
e-x2/2 and the

 multiples of the Hermite polynomials; for details see Kreider et al. (1966).
multiples of the Hermite polynomials; for details see Kreider et al. (1966).
The sample coefficients will then be defined by
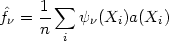
|
but otherwise the estimates will be defined as above; possible estimates are
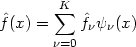
| (2.9) |
or
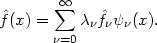
| (2.10) |
The properties of estimates obtained by the orthogonal series method
depend on the details of the series being used and on the system of
weights. The Fourier series estimates will integrate to unity,
provided
 0 = 1, since
0 = 1, since
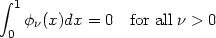
|
and
 0
will always be equal to one. However, except for rather
special choices of the weights
0
will always be equal to one. However, except for rather
special choices of the weights

 ,
,
 cannot
be guaranteed to be non-negative. The
local smoothness properties of the estimates will again depend on the
particular case; estimates obtained from (2.8) will have derivatives of
all orders.
cannot
be guaranteed to be non-negative. The
local smoothness properties of the estimates will again depend on the
particular case; estimates obtained from (2.8) will have derivatives of
all orders.