


2.6. The variable kernel method
The variable kernel method is somewhat related to the nearest neighbour approach and is another method which adapts the amount of smoothing to the local density of data. The estimate is constructed similarly to the classical kernel estimate, but the scale parameter of the 'bumps' placed on the data points is allowed to vary from one data point to another.
Let K be a kernel function and k a positive integer. Define dj, k to be the distance from Xj to the kth nearest point in the set comprising the other n - 1 data points. Then the variable kernel estimate with smoothing parameter h is defined by
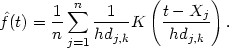
| (2.5) |
The window width of the kernel placed on the point Xj is proportional to dj, k, so that data points in regions where the data are sparse will have flatter kernels associated with them. For any fixed k, the overall degree of smoothing will depend on the parameter h. The choice of k determines how responsive the window width choice will be to very local detail.
Some comparison of the variable kernel estimate with the generalized nearest neighbour estimate (2.4) may be instructive. In (2.4) the window width used to construct the estimate at t depends on the distances from t to the data points; in (2.5) the window widths are independent of the point t at which the density is being estimated, and depend only on the distances between the data points.
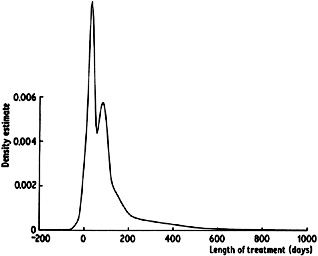
In contrast with the generalized nearest neighbour estimate, the variable kernel estimate will itself be a probability density function provided the kernel K is; that is an immediate consequence of the definition. Furthermore, as with the ordinary kernel estimator, all the local smoothness properties of the kernel will be inherited by the estimate. In Fig. 2.11 the method is used to obtain an estimate for the suicide data. The noise in the tail of the curve has been eliminated, but it is interesting to note that the method exposes some structure in the main part of the distribution which is not really visible even in the undersmoothed curve in Figure 2.9.
|
Fig. 2.11 Variable kernel estimate for suicide study data, k = 8, h = 5. |
In Section 5.3, the variable kernel method will be considered in greater detail, and in particular an important generalization, called the adaptive kernel method, will be introduced.