1.2. Dynamics

Everything discussed so far has been "geometrical", relying only on the form of the Robertson-Walker metric. To make further progress in understanding the evolution of the universe, it is necessary to determine the time dependence of the scale factor a(t). Although the scale factor is not an observable, the expansion rate, the Hubble parameter, H = H(t), is.

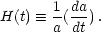(1.8)

The present value of the Hubble parameter, often referred to as the Hubble "constant", is H₀ H(t₀) 100 h km s^-1Mpc^-1 (throughout, unless explicitly stated otherwise, the subscript "0" indicates the present time). The inverse of the Hubble parameter provides an expansion timescale, H₀^-1 = 9.78 h^-1 Gyr. For the HST Key Project (Freedman et al. 2001) value of H₀ = 72 km s^-1Mpc^-1 (h = 0.72), H₀^-1 = 13.6 Gyr.

The time-evolution of H describes the evolution of the universe. Employing the Robertson-Walker metric in the Einstein equations of General Relativity (relating matter/energy content to geometry) leads to the Friedmann equation

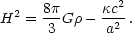(1.9)

It is convenient to introduce a dimensionless density parameter, , defined by

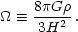(1.10)

We may rearrange eq. 9 to highlight the relation between matter content and geometry

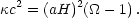(1.11)

Although, in general, a, H, and are all time-dependent, eq. 11 reveals that if ever < 1, then it will always be < 1 and in this case the universe is open ( < 0). Similarly, if ever > 1, then it will always be > 1 and in this case the universe is closed ( > 0). For the special case of = 1, where the density is equal to the "critical density" _crit 3H² / 8 G, is always unity and the universe is flat (Euclidean 3-space sections; = 0).

The Friedmann equation (eq. 9) relates the time-dependence of the scale factor to that of the density. The Einstein equations yield a second relation among these which may be thought of as the surrogate for energy conservation in an expanding universe

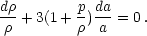(1.12)

For "matter" (non-relativistic matter; often called "dust"), p << , so that / ₀ = (a₀ / a)³. In contrast, for "radiation" (relativistic particles) p = / 3, so that / ₀ = (a₀ / a)⁴. Another interesting case is that of the energy density and pressure associated with the vacuum (the quantum mechanical vacuum is not empty!). In this case p = -, so that = ₀. This provides a term in the Friedmann equation entirely equivalent to Einstein's "cosmological constant" . More generally, for p = w, / ₀ = (a₀ / a)^3(1+w).

Allowing for these three contributions to the total energy density, eq. 9 may be rewritten in a convenient dimensionless form

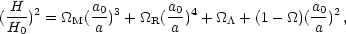(1.13)

where _M + _R + .

Since our universe is expanding, for the early universe (t << t₀) a << a₀, so that it is the "radiation" term in eq. 13 which dominates; the early universe is radiation-dominated (RD). In this case a t^1/2 and t^-2, so that the age of the universe or, equivalently, its expansion rate is fixed by the radiation density. For thermal radiation, the energy density is only a function of the temperature (_R T⁴).