1.2.1. Counting Relativistic Degrees of Freedom

It is convenient to write the total (radiation) energy density in terms of that in the CMB photons

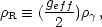(1.14)

where g_eff counts the "effective" relativistic degrees of freedom. Once g_eff is known or specified, the time - temperature relation is determined. If the temperature is measured in energy units (kT), then

(1.15)

If more relativistic particles are present, g_eff increases and the universe would expand faster so that, at fixed T, the universe would be younger. Since the synthesis of the elements in the expanding universe involves a competition between reaction rates and the universal expansion rate, g_eff will play a key role in determining the BBN-predicted primordial abundances.

• Photons

Photons are vector bosons. Since they are massless, they have only two degress of freedom: g_eff = 2. At temperature T their number density is n = 411(T / 2.726K)³ cm^-3 = 10^31.5T_MeV³ cm^-3, while their contribution to the total radiation energy density is = 0.261 (T / 2.726K)⁴ eV cm^-3. Taking the ratio of the energy density to the number density leads to the average energy per photon < E > = / n = 2.70 kT. All other relativistic bosons may be simply related to photons by

(1.16)

The g_B are the boson degrees of freedom (1 for a scalar, 2 for a vector, etc.). In general, some bosons may have decoupled from the radiation background and, therefore, they will not necessarily have the same temperature as do the photons (T_B T).

• Relativistic Fermions

Accounting for the difference between the Fermi-Dirac and Bose-Einstein distributions, relativistic fermions may also be related to photons

(1.17)

g_F counts the fermion degrees of freedom. For example, for electrons (spin up, spin down, electron, positron) g_F = 4, while for neutrinos (lefthanded neutrino, righthanded antineutrino) g_F = 2.

Accounting for all of the particles present at a given epoch in the early (RD) evolution of the universe,

(1.18)

For example, for the standard model particles at temperatures T few MeV there are photons, electron-positron pairs, and three "flavors" of lefthanded neutrinos (along with their righthanded antiparticles). At this stage all these particles are in equilibrium so that T = T_e = T where _e, _µ, . As a result

(1.19)

leading to a time - temperature relation: t = 0.74 T^-2_Mev sec.

As the universe expands and cools below the electron rest mass energy, the e^± pairs annihilate, heating the CMB photons, but not the neutrinos which have already decoupled. The decoupled neutrinos continue to cool by the expansion of the universe (T a^-1), as do the photons which now have a higher temperature T = (11/4)^1/3T (n / n = 11/3). During these epochs

(1.20)

leading to a modified time - temperature relation: t = 1.3 T_Mev^-2 sec.