5.2.1. Using Residual Correlations to Identify Poor Fits Quantitatively

In order to compare the observed residual correlations with the results from the mock catalogs, we would like to define a single statistic that summarizes the deviation of () from unity. Let us define () N_p() () (cf. eq. [25]). In Appendix C, we show that () approximates a Gaussian random variable of mean zero and variance N_p(), if indeed the VELMOD residuals are uncorrelated on scale . [This property was used to compute the error bars on () above.] To the degree this approximation is a good one, the quantity

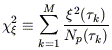
(26)

will be distributed approximately as a ² variable with M degrees of freedom, where M is the number of separate bins in which () is calculated. In contrast, if the residuals are strongly correlated on any scale , ² will exceed its expected value significantly.

However, because a single galaxy will appear in many different pairs in the correlation statistic, both within and between bins in , the assumptions made above do not hold rigorously. In Appendix C, we explore this issue further. For now, we appeal to the mock catalogs to assess how closely the quantity ² follows ² statistics. We computed it for each of the 20 mock catalog runs (Section 3) with _I = 1. We carried out the calculation to a maximum separation of 6400 km s^-1, in bins of width 200 km s^-1, so that M = 32, and found a mean value <²> = 27.83±1.82, which may be compared with an expected value of 32 for a true ² statistic. The rms scatter in ² was 8.15, which is the same as that expected for a true ². The difference between the mean and expected values is 2.3 , indicating that ² is not exactly a ² statistic, for reasons discussed in Appendix C. However, because the departure from true ² statistics is small, ² is a useful statistic for measuring goodness of fit when calibrated against the mock catalogs.

Before presenting ² for the real data, we consider its variation with _I for the mock catalogs. In Figure 18, we plot the average value of ² over the 20 mock catalogs at each value of _I for which VELMOD was run. Although the minimum is at _I = 1, it is not nearly as sharp as is that of the likelihood as function of _I (e.g., Fig. 2); this statistic does not have the power that the likelihood does for measuring _I. Indeed, for a single realization (the open symbols), the statistic has several local minima. However, it is apparent that a ² value much greater than its expected true value of ~ 28 will indicate a poor fit of the model to the data.

Figure 18. Residual correlation statistic 2, defined by eq. (26), plotted as a function of I for the mock catalogs. The filled symbols show an average over 20 mock catalogs; the open symbols show the values obtained for a single mock catalog.

In Figure 19, we plot the statistic ² as a function of _I for the real data, with and without the quadrupole included. The horizontal lines indicate the expected value of ², and the 1 and 3 deviations from it. Note first that the no-quadrupole model does not provide an acceptable fit for any value of _I. This is not a conclusion we could have reached on the basis of the likelihood analysis alone. When the quadrupole is included, the only values of _I that are unambiguously ruled out are _I = 0.1, 0.2, and 1.0. The best-fit model according to VELMOD, _I = 0.5 plus quadrupole, also has the smallest value of ². Given the multiple minima seen for one mock realization in Figure 18, this is not necessarily deeply significant. The statistic ² is suitable for identifying models that do not fit the data, but it does not have the power of the likelihood statistic for discriminating among those models that do fit.

Figure 19. Residual autocorrelation statistic 2, defined by eq. (26), plotted as a function of I for the real data, with and without the quadrupole modeled. The heavy solid line shows the expected value of the statistic, which was determined by averaging the derived value for 20 mock catalogs. The dot-dashed line and the dashed line show 1 and 3 deviations from this value, respectively. Note that when the quadrupole is not modeled, highly significant residual correlations are detected for all values of I. (The no-quadrupole points for I = 0.1 and 0.2 are not shown because their 2 values are too large.)