Copyright © 1998 by Annual Reviews. All rights reserved
| Annu. Rev. Astron. Astrophys. 1998. 36:
599-654 Copyright © 1998 by Annual Reviews. All rights reserved |
2.6. Biased Galaxy Formation
Biased galaxy formation refers to phenomenological models of galaxy formation in simulations (or analytic theories) that lack sufficient resolution or physical content to allow galaxies to form directly. Crudely speaking, "bias" as used in this context refers to the difference between the galaxy distribution and that of all matter. Although the current trend is toward more realistic modeling of galaxy formation, biasing models are still used in large-box N-body simulations, analytic theories, and analysis of redshift survey data. For these reasons, we include a brief discussion to conclude this section on numerical simulation algorithms.
Bias was originally invoked to explain the stronger correlations of galaxy clusters compared with galaxies themselves. Kaiser (1984) showed that the regions of high density (plausibly those regions that preferentially form galaxies) in a Gaussian random field are more strongly correlated than the overall field itself. Dekel & Rees (1987) reviewed the motivation and physical mechanisms for biased galaxy formation. In recent years, bias has been used most commonly in the context of the linear bias model, where, on scales larger than a few megaparsecs, the galaxy density fluctuations are enhanced over those of the mass by a factor b, the linear bias factor:
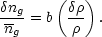 |
(11) |
Local nonlinear biasing models were investigated by Coles (1993). Mo & White (1996), Kauffmann et al (1997) devised an analytic model of bias based on the Press-Schechter formalism.
Bardeen et al (1986) proposed that galaxy formation occurs at the peaks of the initial density field smoothed on a galactic mass scale. This "peak bias" model has been used in N-body simulations to tag a fraction of particles as galaxies (Davis et al 1985, Park 1991, Suginohara & Suto 1991). White et al (1987a) found that bias arose naturally when enough resolution was present to identify dense dark matter halos forming within the simulations. However, Katz et al (1993) showed that the association between dense halos and initial peak particles is poor. Moreover, beginning with Carlberg & Couchman (1989), many groups have found that the halos formed in dark matter simulations are actually antibiased with respect to the mass, i.e. b < 1, because of excessive merging of halos compared with real galaxies. They also showed that the root-mean-square (rms) velocities of dark matter halos may be substantially less than those of the mass, a phenomenon called cosmological velocity bias (Couchman & Carlberg 1992, Summers et al 1995).
While biased galaxy formation remains a useful phenomenological model, recent emphasis has shifted toward cosmological simulations with gas and cooling where dense baryonic clumps plausibly representing galaxies form without need for a biasing model. Indeed such simulations permit the measurement of the biasing factor (or scale-dependent bias function) itself (e.g. Cen & Ostriker 1992a, Tissera et al 1994, Summers et al 1995, Gnedin 1996b). Although numerical simulation of galaxy formation will always rely on phenomenological treatments of star formation and stellar energy feedback processes, these are considerably more direct and physical than current biased galaxy formation models and may one day obviate the need for biasing schemes.