Copyright © 1998 by Annual Reviews. All rights reserved
| Annu. Rev. Astron. Astrophys. 1998. 36:
599-654 Copyright © 1998 by Annual Reviews. All rights reserved |
Cosmic structure formation models are stochastic: The initial conditions are random (albeit with well-specified statistical properties), and their evolution is chaotic. No realistic model would claim to predict the exact structures we see in our Universe; at best, theorists can hope to construct models of the Universe that "look like" the real thing. But how is this vague test quantified? Many statistics have been devised for this purpose. In this section, a brief summary of methods is presented; a more complete review was given by Coles (1992).
Table 1 lists the major statistics applied in
cosmological simulations
of structure formation. They are distinguished by whether they are most
naturally applied to continuous fields such as the density fluctuation
field  (
(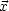 ) or to a set of
discrete points
(e.g. galaxies or simulation particles). In practice these applications are
interchangeable because a point set can be convolved with a window
function to produce a continuous field, and a continuous field may be
Poisson sampled (with spatially-varying Poisson density) to produce a
point set (e.g.
Bertschinger 1992).
Other statistics apply exclusively
to the internal properties of galaxies, clusters, or dark matter halos.
Some statistical measures associated with specific physical measurements
(e.g. the column density distribution of
Ly
) or to a set of
discrete points
(e.g. galaxies or simulation particles). In practice these applications are
interchangeable because a point set can be convolved with a window
function to produce a continuous field, and a continuous field may be
Poisson sampled (with spatially-varying Poisson density) to produce a
point set (e.g.
Bertschinger 1992).
Other statistics apply exclusively
to the internal properties of galaxies, clusters, or dark matter halos.
Some statistical measures associated with specific physical measurements
(e.g. the column density distribution of
Ly absorption lines
or the distribution of gravitational lens separations) are discussed
in Section 5.
absorption lines
or the distribution of gravitational lens separations) are discussed
in Section 5.
| Category | Statistic | Name | Reference |
| Particle positions |  (r) (r) |
Two-point correlation function | Peebles 1980 |
| P(k) | Power spectrum | Bertschinger 1992 | |
 (r1, r2,
r3) (r1, r2,
r3) |
Three-point correlation function | Groth & Peebles 1977 | |
| B(k1, k2, k3) | Bispectrum | Peebles 1980 | |
 N, N, 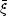 N N |
N-point correlation functions and moments | Peebles 1980 | |
| P0(V), PN(V) | Void probability function, cell counts | White 1979 | |
| - | Percolation, minimal spanning tree statistics | Coles 1992 | |
| - | Multifractal statistics | Martínez et al 1990 | |
| Density fields | G( ) ) |
Genus of isodensity surfaces | Melott 1990 |
| - | Area of isodensity surfaces | Ryden 1988 | |
vi( ) ) |
Minkowski functionals | Mecke et al 1994 | |
f
( ) ) |
One-point density distribution | Kofman et al 1994 | |
< Nc> Nc> |
One-point cumulants (skewness, kurtosis, etc) | Peebles 1980 | |
| - | Shape statistics | Davé et al 1997b | |
| Velocity fields | f(v) | One-point velocity distribution (and moments) | Inagaki et al 1992 |
 |
Mach number | Ostriker & Suto 1990 | |
f( ) ) |
Velocity divergence distribution (and moments) | Bernardeau et al 1985 | |
f(v12),
 12 12 |
Pairwise radial velocity distribution and dispersion | Davis & Peebles 1983 | |
| Redshift space |  (rp, (rp,
 ), ),
 (s) (s) |
Redshift space correlation functions | Davis & Peebles 1983 |
| Ps(k, µ) | Redshift space power spectrum | Cole et al 1995 | |
| Clusters or halos | n(m) | Mass distribution | Press & Schechter 1974 |
| n(Vc) | Circular velocity distribution | Gelb & Bertschinger 1994a | |
n( ) ) |
Velocity dispersion distribution | Evrard 1989 | |
| n(T), n(L) | Temperature and X-ray luminosity distributions | Cen & Ostriker 1994a | |