Annu. Rev. Astron. Astrophys. 1998. 36: 599-654 Copyright © 1998 by Annual Reviews. All rights reserved

3.1. Statistics Using Particle Positions

The spatial properties of a statistically homogeneous set of points (galaxies or simulation particles) is fully characterized by the N-point correlation functions (Peebles 1980). The best known of these is the two-point correlation function, which is measured to be well fit by a power-law (r) = (r / r₀) with = 1.8 and r₀ 5 h^-1 Mpc (Totsuji & Kihara 1969;, Peebles 1980 and references therein). This statistic has been widely used in cosmic structure formation simulations beginning with those of Miyoshi & Kihara (1975). The standard method to compute is based on counting pairs as a function of pair separation, with subsampling if the total number of pairs is prohibitively large; Ruffa & Porter (1993) devised a fast algorithm based on a tree code. Simulations not only use the correlation function as a comparative statistic, they also can test the reliability of estimators of applied to observational samples (e.g. Mo et al 1992). The three-point correlation function can be measured in simulations by counting triplets (e.g. Efstathiou & Eastwood 1981), but higher-order correlations are more efficiently estimated and characterized by their volume averages, the irreducible moments (cumulants) of counts in cells 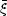_N (Peebles 1980).

The power spectrum and two-point correlation function are Fourier transform pairs. From this fact, the incorrect conclusion may be reached that they are interchangeable in practice. Estimates of the two-point correlation function require subtracting off the number of pairs for a Poisson distribution. This requires knowing the mean density accurately when the correlation amplitude is low, i.e. on large scales. Large-scale sample variations ("cosmic variance") make it difficult to estimate this density in any finite-size survey (but see Hamilton 1993 for an estimator that is relatively insensitive to this effect). The correlation function is most accurately measured in the strong-clustering regime, > 1. The power spectrum estimate involves no such subtraction of unclustered pairs; therefore it offers a reliable estimate of clustering to the longest wavelengths probed by a survey, subject to the caveat of cosmic variance (i.e. sampling fluctuations) and to practical details of sample geometry. The power spectrum is widely used as a measure of structure in numerical simulations as well as for comparison with observations (e.g. Gramann & Einasto 1992, Vogeley et al 1992, Baugh & Efstathiou 1994). The Fourier transform of the three-point correlation function is known as the bispectrum (e.g. Fry et al 1993).

The distribution of counts in cells, P_N (V), gives the probability of finding N objects in a randomly placed volume V of fixed shape. This set of statistics provides an alternative and very useful characterization of clustering. Interest in this cell count distribution grew after a simple prediction of its form was made by Saslaw & Hamilton (1984), based on a thermodynamic theory of gravitational clustering (see Sheth & Saslaw 1996 for a refinement of the theory). Although the thermodynamic theory has been met with skepticism, it has spurred the development of many alternative hierarchical scaling theories as well as their investigation in cosmological simulations (e.g. Itoh et al 1988, Suto et al 1990, Bouchet & Hernquist 1992, Ueda et al 1993, Bromley 1994, Colombi et al 1995, Ueda & Yokoyama 1996).

The void probability function P₀ (V) contains information about all 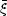_N and is fully determined by them when these moments exist (White 1979). (Here "void" should not be thought of in the sense of the large underdense regions of the galaxy distribution. Instead it refers to any volume that contains no objects - galaxies or simulation particles - whatsoever. Observationally, of course, a luminosity limit must be stated to make this statement meaningful.) The void probability function has been studied extensively in numerical simulations combined with analytical models of hierarchical clustering (e.g. Bouchet et al 1991, Einasto et al 1991, Weinberg & Cole 1992, Colombi et al 1996a).

Additional statistics of point processes are provided by percolation analysis (Zel'dovich et al 1982) and related statistics based on the minimal spanning tree (Pearson & Coles 1995, Bhavsar & Splinter 1996;, Krzewina & Saslaw 1996 and references therein). These approaches "connect the dots" with short line segments. There has been considerable discussion about the utility of percolation as a cosmological test, with some authors (e.g. Bhavsar & Barrow 1983, Dekel & West 1985) emphasizing difficulties and expressing doubts about its discriminating power, while others maintain its value (Dominik & Shandarin 1992, Yess & Shandarin 1996). Recently Sahni et al (1997) have proposed an extension of percolation, the volume fraction of the largest cluster or void defined at a given density threshold, that addresses some of the practical problems of the percolation length and relates percolation to topology.

The hierarchical scaling of correlation functions has inspired comparisons with statistical fractals (Peebles 1980 and references therein). The galaxy distribution cannot be a simple fractal because strong clustering on small scales gives way to homogeneity on large scales; the distribution is not scale invariant. However, over a limited range of scales it may be a multifractal, a clustered distribution having different scaling properties as a function of density (e.g. Jones et al 1988, Martínez et al 1990). Analytical theories and simulations (e.g. Bouchet et al 1991) suggest that there are two scalings, one for voids and one for clusters, described by the Hausdorff and correlation dimensions, respectively. Colombi et al (1992) gave an excellent summary of the numerical, statistical, and dynamical issues involved in testing whether the matter distribution in simulations (and, by extension, the Universe) is a bifractal.