Inflation and the CMB - C.H. Lineweaver

3.1. Friedmann's Equation Exponential Expansion

One way to describe inflation is that during inflation, a Lambda _inf term dominates Eq. 11. Thus, during inflation we have,

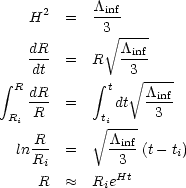$\begin{eqnarray} H^{2} &=& \frac{\Lambda_{\rm inf}}{3}\\ \frac{dR}{dt} &=& R\sqrt{\frac{\Lambda_{\rm inf}}{3}}\\ %\frac{dR}{R} &=& dt\sqrt{\frac{\Lambda_{inf}}{3}}\\ \int^{R}_{R_{i}}\frac{dR}{R} &=& \int^{t}_{t_{i}}dt\sqrt{\frac{\Lambda_{\rm inf}}{3}}\\ ln \frac{R}{R_{i}} &=& \sqrt{\frac{\Lambda_{\rm inf}}{3}}\;(t - t_{i})\\ R &\approx & R_{i} e^{Ht} \end{eqnarray}$

(22)

(23)

(24)

(25)

(26)

where t_i and R_i are the time and scale factor at the beginning of inflation. To get Eq. 26 we have assumed 0 approx t_i << t < t_e (where t_e is the end of inflation) and we have used Eq. 22. Equation 26 is the exponential expansion of the Universe during inflation. The e-folding time is 1/H. The doubling time is (ln 2) / H. That is, during every interval Delta t = 1/H, the size of the Universe increases by a factor of e = 2.718281828... and during every interval Delta t = (ln 2) / H the size of the Universe doubles.