The Age of the Galactic Globular Cluster System

Annu. Rev. Astron. Astrophys. 1996. 34: 461-510
Copyright © 1996 by Annual Reviews. All rights reserved

3. GLOBULAR CLUSTER DISTANCES

Given that the most reliable indicator of a globular cluster's age is its turnoff luminosity, the determination of precise distances to these systems is arguably the single most crucial observational input into the evaluation of accurate ages (see, e.g. Renzini 1991, Chaboyer 1995, Bolte & Hogan 1995). Nearly everything that we know about GC distances is based on two standard candles - namely, the nearby subdwarfs and the RR Lyrae variable stars. Thanks to the development of the Hubble Space Telescope (HST), we will soon be able to add white dwarfs to this very short list. These stars have the advantage of being essentially free of metallicity and convection complications (cf Fusi Pecci & Renzini 1979), and local white dwarf calibrators are much more numerous than subdwarfs. Although we can anticipate that the fitting to white dwarf cooling sequences will involve a number of difficulties (some unanticipated), it is encouraging that the first HST results, for M4 by Richer et al (1995), indicate a distance very similar to the one adopted by Richer & Fahlman (1984) on the assumption that M_V(HB) = 0.84. These results lead to their determination of an age of 13-15 Gyr for this cluster. We also recognize the potential of direct astrometric methods (see Cudworth & Peterson 1988, Rees 1992) and the existence of a number of other approaches (e.g. using the RGB tip magnitude) to constrain cluster distances. We, however, restrict the present discussion to the two classical distance calibrators.

3.1. Subdwarf-Based Distances

The nearby subdwarfs - metal-poor stars with halo kinematics whose orbits have brought them near enough to the Sun for them to have measurable trignometric parallaxes - play two critical roles in the measurement of GC ages. First, with well-determined values of M_V, these objects provide a direct test of the model predictions for the position of the zero-age main-sequence as a function of [Fe/H] in the low-metallicity regime. Second, under the (testable) assumption that the subdwarfs are local versions of the unevolved main-sequence stars in globular clusters, they can be used to tie the cluster distances directly into the most reliable distance scale that exists in extra-Solar-system astronomy (that defined by trignometric parallaxes).

The recognition of the importance of the subdwarfs and of their relation to the RR Lyraes and the halo GCs is itself an interesting story (see the review by Sandage 1986). An important landmark was Sandage's (1970) identification of eight subdwarfs with sufficiently good measures for them to be useful for deriving the distances to GCs. He also used them to calibrate the absolute magnitude of the horizontal branch at the position of the instability strip in M3, M15, and M92. Carney (1979), Laird, Carney & Latham (1988) improved the [Fe/H] determinations of that sample. In the pre-CCD era of photometry, however, the subdwarfs were of limited usefulness for establishing the Population II distance scale because of fairly large random and (in retrospect) scale errors in the measurement of faint main-sequence cluster stars [see, e.g. Figure 4 in Fahlman, Richer & VandenBerg (1985) and Figure 30 in Stetson & Harris (1988)]. CMDs derived from CCD data, beginning in the mid-1980s, made the adoption of a subdwarf-based distance scale a much more viable alternative to purely HB-based distance estimates. With CCDs and 4-m telescopes, the main sequences of nearby clusters could be defined very accurately down to M_V ~ 10 (e.g. see Figure 36 in Stetson & Harris 1988). In the CCD era, the limiting factors in the derivation of cluster distances via subdwarf fitting became the scatter in the Population II main-sequence fiducial defined by the subdwarfs and the lingering uncertainties in the reddening and color calibrations of the cluster data.

Table 1 contains our compilation of relevant data for all stars in the 1991 edition of the Yale Trigonometric Parallax Catalogue with sigma / < 0.5 and spectroscopic measures of [Fe/H] ltapprox -1.3. This list includes the original eight stars from Sandage (1970) minus HD 140283, which appears to be an evolved star (Magain 1989, Dahn 1994), plus an additional eight stars, which generally have large sigma values. The tabulated sigma values were taken from the Yale Catalogue; the apparent colors and magnitudes are from the compilation given in the Hipparcos Input Catalogue (Turon et al 1992). The absolute magnitudes were calculated from the usual equation: M_V = V + 5 + 5log(). Because trignometric parallax measurements are subject to a Malmquist-like bias, arising from the coupling of the measuring errors with the steep slope of the true parallax distribution, there is a tendency for the observed parallaxes to be larger than their actual values. (This is true in the statistical sense for entire catalogues as well as for individual measurements.) The resultant so-called Lutz-Kelker (or L-K) corrections (Lutz & Kelker 1973) were determined to compensate for this effect. To be specific, we have applied the correction delta M_V = -5.43( sigma / )² - 25.51( sigma / )⁴, according to the formulation of Hanson (1979), who used the distribution of proper motions of objects in the parallax catalogues to estimate the magnitudes of the L-K corrections. This expression for delta M_V is strictly valid only for sigma / < 0.33. (The always-negative L-K corrections are added to the M_V values because the true luminosities are larger than the uncorrected estimates.)

**Table 1.** Subdwarfs with and [Fe/H] determinations

ID	[Fe/H]	V	B - V	(")	(")	M_V	(M_V)	M_V(L-K)	(B - V)_-2.14

HD 7808	-1.78	9.746	1.008	0.0663	0.0126	8.854	0.412	8.624	0.974
HD 19445	-2.08	8.053	0.475	0.0252	0.0052	5.060	0.448	4.783	0.471
HD 25329	-1.34	8.506	0.863	0.0548	0.0047	7.200	0.186	7.159	0.800
HD 64090	-1.73	8.309	0.621	0.0405	0.0023	6.346	0.123	6.328	0.591
HD 74000	-2.20	9.62	0.43	0.0155	0.0048	5.572	0.672	4.816	0.434
HD 84937	-2.12	8.324	0.421	0.0280	0.0064	5.560	0.496	5.206	0.420
HD 103095	-1.36	6.442	0.754	0.1127	0.0016	6.702	0.031	6.701	0.693
HD 134439	-1.4	9.066	0.770	0.0365	0.0025	6.877	0.149	6.851	0.714
HD 134440	-1.52	9.445	0.850	0.0365	0.0025	7.256	0.149	7.230	0.804
HD 149414	-1.39	9.597	0.736	0.0281	0.0035	6.841	0.270	6.750	0.679
HD 194598	-1.34	8.345	0.487	0.0194	0.0014	4.784	0.157	4.755	0.424
HD 201891	-1.42	7.370	0.508	0.0325	0.0027	4.929	0.180	4.891	0.462
HD 219617	-1.4	8.160	0.481	0.0280	0.0055	5.396	0.426	5.148	0.431
BD+66 268	-2.06	9.912	0.667	0.0216	0.0026	6.584	0.261	6.500	0.661
BD+11 4571	-3.6	11.170	1.060	0.0316	0.0047	8.668	0.323	8.536	1.080

The last column in Table 1 contains the predicted color that each star would have if its metallicity were [Fe/H] = -2.14 (chosen to illustrate the subdwarf-fitting procedure for the specific case of M92). At a fixed mass, main-sequence stars of different [Fe/H] will encompass a range in color and M_V; consequently, to define a fiducial for distance determinations by the main-sequence fitting technique using subdwarfs, it has become common practice to derive a mono-metallicity subdwarf sequence. This is obtained by correcting the color of each subdwarf, at its observed M_V, by the difference between the predicted colors of stars with the [Fe/H] of the subdwarf and that of the cluster itself. Thus, the model colors are used only differentially. Bi-cubic interpolation through a table of B - V colors at different [Fe/H] and M_V values, generated from the Bergbusch & VandenBerg (1992) isochrones, was used to generate the color corrections: These take into account the dependence of radius on metallicity at fixed luminosity as well as purely atmospheric line blanketing effects.

Figure 7 shows how well 16 Gyr, [ alpha /Fe] = 0.3 isochrones for [Fe/H] = -1.31, -1.71, and -2.14 (from VandenBerg et al 1996 ⁵) coincide with the positions of the local subdwarfs on the color-magnitude plane. We have plotted all of the stars in Table 1 (specifically, the data in the fourth, eighth, and ninth columns) whose metallicities fall within ± 0.15 dex of the isochrone [Fe/H] values. The agreement is about as good as one could hope for. Note, in particular, how well the models satisfy the constraint provided by the best of the subdwarfs (HD 103095, also called Groombridge 1830) and that the lower metal abundance subdwarfs tend to be displaced from those of higher Z in roughly the direction and amount suggested by the theory.

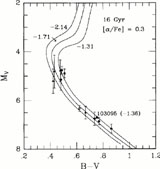Figure 7. Comparison of the CMD locations of the nearby subdwarfs, whose properties are in the fourth, eighth, and ninth columns of Table 1, with VandenBerg et al (1996) isochrones. The closed circles, open circle, and closed triangles represent those subdwarfs whose tabulated [Fe/H] values are within ± 0.15 dex of those of the three isochrones; namely, -1.31, -1.71, and -2.14, respectively. All of the isochrones assume [ alpha /Fe] = 0.3 and an age of 16 Gyr, though the latter choice is inconsequential.

A main-sequence fit of M92 to the subdwarfs, using the data in the eighth, ninth, and tenth columns of Table 1 for those stars with sigma (M_V) < 0.3 mag, is illustrated in Figure 8. When a foreground reddening of 0.02 mag (see Stetson & Harris 1988) is assumed, an apparent distance modulus of 14.65 mag is obtained. The VandenBerg et al (1996) isochrones, for the indicated parameters, have simply been overlayed on this figure, i.e. no color adjustments of any kind have been applied to them. [Their temperature and color scales are very close to those of the Bergbusch & VandenBerg (1992) calculations, which were used to produce the B - V data in the last column of our table.] One has the impression that a small redward color shift should be applied to the isochrones at the fainter magnitudes, but what differences exist are clearly small.

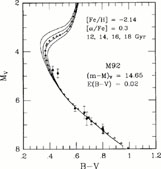Figure 8. Main-sequence fit of the Stetson & Harris (1988) M92 main-sequence fiducial (open triangles) to the subdwarfs (closed circles), after the colors of the latter have been adjusted to compensate for differences between their [Fe/H] values and that of the cluster (see text). These revised colors are as given in the last column of Table 1. Only those data for which sigma (M_V) < 0.3 mag have been plotted. VandenBerg et al (1996) isochrones for the indicated chemical composition and ages have been overlayed onto (not fitted to) the observations.

An age of 15.5-16 Gyr is indicated from the observed location of the turnoff and subgiant branch relative to their theoretical counterparts. Allowing for helium diffusion would reduce this estimate to approx 15 Gyr (see Section 2.2.1), which should not be in error by more than ± 1.5 Gyr due to chemical composition uncertainties (see Section 2.4). According to Section 2.1.3, it is possible that deficiencies in convection theory could contribute a small age uncertainty, but other than this minor concern, remaining uncertainties in stellar physics should have little impact. Assuming no systematic error in the distance scale defined by the L-K corrected trigonometric parallax measures, the M92 distance modulus error is dominated by three terms [see Stetson & Harris (1988) for a more complete discussion of the errors associated with the subdwarf fit]. There is a goodness-of-fit term, which we approximate with the RMS vertical scatter (after correcting the colors to [Fe/H] = -2.14) of the subdwarf distribution around the distance-modulus-adjusted M92 main-sequence; a term for the uncertainty in the reddening towards M92,

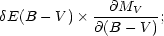$\begin{displaymath} \delta E (B - V) \times \frac{\partial M_V}{\partial (B - V)} ; \end{displaymath}$

and a term for the uncertainty in the [Fe/H] value for M92 stars,

$\begin{displaymath} \delta [Fe / H] \times \frac{\partial M_V}{\partial (B - V)} \times \frac{\partial (B - V)}{\partial [Fe / H]} . \end{displaymath}$

If we take delta E(B - V) ~ 0^m.02 and delta [Fe/H] ~ 0.2 dex, then these three terms added in quadrature give sigma (m - M) ~ 0^m.16, which translates into an uncertainty in the age of ~ 2.0 Gyr (68% confidence interval). The delta [Fe/H] term enters the age uncertainty a second time because M_bol(TO) has an [Fe/H] dependence, and the formal observational uncertainty in the age that we derive for M92, assigning no errors to the models and assuming the subdwarf distances have no systematic errors, is 2.2 Gyr.

⁵ We make fairly extensive use of these calculations in this study, obviously because they are immediately at hand, but also because they represent the most up-to-date models presently available. In particular, they employ opacities for the adopted alpha / Fe number abundance ratios and are not based on the renormalization of scaled-solar-mix calculations, as has been advocated by Salaris et al (1993). Their procedure does appear to work well at low Z values, but not for Z < 0.002 (or so) according to VandenBerg et al (1996; also see Weiss, Peletier & Matteucci 1995): At high Z, the RGB location becomes insensitive to [ alpha / Fe]. Importantly, as shown by VandenBerg (1992), Salaris et al, and the three lowermost curves in Figure 1 of this paper, virtually identical results are obtained when completely independent codes employing similar physics are used. Back.