B.6.3. Cross Sections

The basic quantity we need for any statistical analysis is the cross section of the lens for producing the desired lensing effect (e.g. multiple images, two images, bright images...). The simplest cross section is the multiple imaging cross section of the SIS lens - the angular area on the source plane in which a source will produce two lensed images. We know from Eqns. B.21 and B.22 that the source must lie within Einstein radius b of the lens center to produce multiple images, so the cross section is simply _SIS = b². Since the Einstein radius b = 4(_v / c)² D_ls / D_s depends on the velocity dispersion and redshift of the lens galaxy, we will need a model for the distribution of lenses in redshift and velocity dispersion to estimate the optical depth for lensing. If we are normalizing directly to stellar dynamical measurements of lenses, then we will also need a dynamical model (e.g. the Jeans equations of Section B.4.9) to relate the observed stellar velocity dispersions to the characteristic dark matter velocity dispersion _v appearing as a parameter of the SIS model. We can also compute cross sections for obtaining different image morphologies. For example, in Eqn. B.32 we calculated the caustic boundaries for the four-image region of an SIS in an external shear . If we integrate to find the area inside the caustic we obtain the four-image cross section

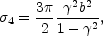(B.104)

while (provided || < 1/3) the two-image cross section is ₂ = _SIS - _{4 SIS}. If the shear is larger, then the tips of astroid caustic extend beyond the radial (pseudo-)caustic and the lens has regions producing two images, three images in the disk geometry (Fig. B.18), and four images with no simple expression for the cross sections. There are no analytic results for the singular isothermal ellipsoid (Eqn. B.37 with s = 0), but we can power expand the cross section as a series in the ellipticity to find at lowest order that

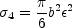(B.105)

for a lens with axis ratio q = 1 - , while the total cross section is _SIS = b² (e.g. Kochanek [1996b], Finch et al. [2002]). As a general rule, a lens of ellipticity is roughly equivalent to a spherical lens in an external shear of /3. According to the cross sections, the fraction of four-image lenses should be of order ₄ / _SIS ~ ² ~ ( / 3)² ~ 0.01 rather than the observed 30%. Most of this difference is a consequence of the different magnification biases of the two image multiplicities.

There is an important subtlety when studying lens statistics with models covering a range of axis ratios, namely that the definition of the critical radius b in (say) the SIE model (Eqn. B.37) depends on the axis ratio and exactly what quantity you are holding fixed in your calculation (see Keeton, Kochanek & Seljak [1997], Keeton & Kochanek [1998], Rusin & Tegmark [2001], Chae [2003]). For example, if we compare a singular isothermal sphere to a face on Mestel disk with the same equatorial circular velocity, the Einstein radius of the disk is 2 / smaller than the isothermal sphere because for the same circular velocity a disk requires less mass than a sphere. Since we usually count galaxies locally and translate these counts into a dynamical variable, this means that lens models covering a range of ellipticities must be normalized in terms of the same dynamical variables as were used to count the galaxies.

Much early effort focused of the effects of adding a finite core radius to these standard models (e.g. Blandford & Kochanek [1987b], Kochanek & Blandford [1987], Kovner [1987a], Hinshaw & Krauss [1987], Krauss & White [1992], Wallington & Narayan [1993], Kochanek [1996a]). The core radius s leads to an evolution of the caustic structures (see Part 1, Blandford & Narayan [1986]) with the ratio between the core radius and the critical radius s / b. Strong lenses with s / b << 1 act like singular models. Weak, or marginal, lenses with s / b ~ 1 have significantly reduced cross sections but higher average magnifications such that the rising magnification bias roughly balances the diminishing cross section to create a weaker than expected effect of core radii on the probability of finding a lens (see Kochanek [1996a]). As the evidence that lenses are effectively singular has mounted, interest in these models has waned, and we will not discuss them further here. There is some interest in these models as a probe of large separation lenses due to groups and clusters where a finite core radius is replaced by effects of the shallow r^-1 NFW density cusp, and we will consider this problem in Section B.7 where we discuss large separation lenses.