3.5. Clusters of galaxies

A cluster of galaxies is a large collection of galaxies held together by their mutual gravitational attraction. The largest ones are around 10¹⁵ solar masses, and are the largest gravitationally-bound structures in the Universe. Even at the present epoch they are relatively rare, with only a few percent of galaxies being in clusters. They provide various ways to study the cosmological parameters; here we discuss constraints from the measurements of the cluster number density and the baryon fraction in clusters.

3.5.1. Cluster number density

The first objects of a given kind form at the rare high peaks of the density distribution, and if the primordial density perturbations are Gaussian-distributed, their number density is exponentially sensitive to the size of the perturbations, and hence can strongly constrain it. Clusters are an ideal application in the present Universe. They are usually used to constrain the amplitude ₈, as a box of side 8 h^-1 Mpc contains about the right amount of material to form a cluster. The most useful observations at present are of X-ray emission from hot gas lying within the cluster, whose temperature is typically a few keV, and which can be used to estimate the mass of the cluster. A theoretical prediction for the mass function of clusters can come either from semi-analytic arguments or from numerical simulations. At present, the main uncertainty is the relation between the observed gas temperature and the cluster mass, despite extensive study using simulations. A recent analysis [29] gives

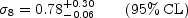
(1.15)

for _m = 0.35, with highly non-Gaussian error bars, but different authors still find a spread of values. Scaling to lower _m increases ₈ somewhat, and the result above is consistent with values predicted in cosmologies compatible with WMAP.

The same approach can be adopted at high redshift (which for clusters means redshifts approaching one) to attempt to measure ₈ at an earlier epoch. The evolution of ₈ is primarily driven by the value of the matter density _m, with a sub-dominant dependence on the dark energy density. It is generally recognized that such analyses favor a low matter density, though there is not complete consensus on this, and at present this technique for constraining the density is not competitive with the CMB.

3.5.2. Cluster baryon fraction

If clusters are representative of the mass distribution in the Universe, the fraction of the mass in baryons to the overall mass distribution would be f_b = _b / _m. If _b, the baryon density parameter, can be inferred from the primordial nucleosynthesis abundance of the light elements, the cluster baryon fraction f_b can then be used to constrain _m and h (e.g., Ref. [30]). The baryons in clusters are primarily in the form of X-ray-emitting gas that falls into the cluster, and secondarily in the form of stellar baryonic mass. Hence, the baryon fraction in clusters is estimated to be

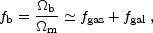
(1.16)

where f_b = M_b / M_grav, f_gas = M_gas / M_grav, f_gal = M_gal / M_grav, and M_grav is the total gravitating mass.

This can be used to obtain an approximate relation between _m and h:

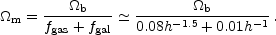
(1.17)

Big Bang Nucleosynthesis gives _b h² 0.02, allowing the above relation to be approximated as _m h^0.5 0.25 (e.g., Ref. [31]). For example, Allen et al. [32] derived a density parameter consistent with _m = 0.3 from Chandra observations.