C. External Shocks

1. Hydrodynamics

Consider the situation when a cold relativistic shell (whose internal energy is negligible compared to the rest mass) moves into the cold ISM. Generally, two shocks form: an outgoing shock that propagates into the ISM or into the external shell, and a reverse shock that propagates into the inner shell, with a contact discontinuity between the shocked material (see Fig. 22).

There dual shocks system is divided to four distinct regions (see Fig. 22): the ambient matter at rest (denoted by the subscript 1), the shocked ambient matter which has passed through the forward shock (subscript 2 or f), the shocked shell material which has passed through the reverse shock (subscript 3 or r), and the unshocked material of the shell (subscript 4). The nature of the emitted radiation and the efficiency of the cooling processes depend on the conditions in the shocked regions 2 and 3. Both regions have the same energy density e. The particle densities n₂ and n₃ are, however, different and hence the effective "temperatures," i.e. the mean Lorentz factors of the random motions of the shocked protons and electrons, are different.

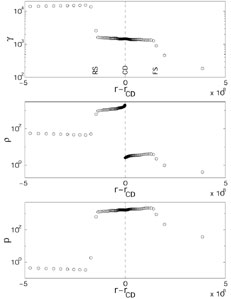Figure 22. The Lorentz factor , the density and the pressure p in the shocks. There are four regions: the ISM (region 1), the shocked ISM (region 2), the shocked shell (region 3) and the un-shocked shell (region 4), which are separated by the forward shock (FS), the contact discontinuity (CD) and the reverse shock (RS). From [194].

Two quantities determine the shocks' structure: , the Lorentz factor of the motion of the inner expanding matter (denoted 4) relative to the outer matter (the ISM or the outer shell in the case of internal collisions - denoted 1) , and the ratio between the particle number densities in these regions, n₄ / n₁. Initially the density contrast between the spherically expanding shell and the ISM is large. Specifically n₄ / n₁ > ². This happens during the early phase of an external shock when the shell is small and dense. This configuration is denoted "Newtonian" because the reverse shock is non-relativistic at most (or mildly relativistic). In this case all the energy conversion takes place in the forward shock. Only a negligible fraction of the energy is converted to thermal energy in the reverse shock if it is Newtonian [368]. Let ₂ be the Lorentz factor of the motion of the shocked fluid relative to the rest frame of the fluid at 1 and let 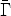₃ be the Lorentz factor of the motion of this fluid relative to the rest frame of the relativistic shell (4):

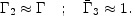(52)

The particle and energy densities (n, e) in the shocked regions satisfy:

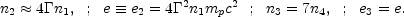(53)

Later, the shell expands and the density ratio decreases (like R^-2 if the width of the shell is constant and like R^-3 if the shell is spreading) and n₄ / n₁ < ² (but n₄ / n₁ > 1). In this case both the forward and the reverse shocks are relativistic. The shock equations between regions 1 and 2 combined with the contact discontinuity between 3 and 2 yield [30, 31, 305]:

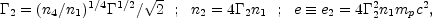(54)

Similar relations hold for the reverse shock:

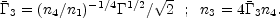(55)

Additinally,

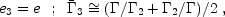(56)

which follow from the equality of pressures and velocity on the contact discontinuity. Comparable amounts of energy are converted to thermal energy in both shocks when both shocks are relativistic.

The interaction between a relativistic flow and an external medium depends on the Sedov length that is defined generally as:

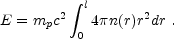(57)

The rest mass energy within the Sedov sphere equals the energy of the explosion. For a homogeneous ISM:

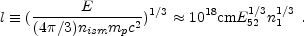(58)

Note that in this section E stands for the isotropic equivalent energy. Because of the very large Lorentz factor angular structure on a scale larger than ^-1 does not influence the evolution of the system and it behaves as if it is a part of a spherical system. A second length scale that appears in the problem is , the width of the relativistic shell in the observer's rest frame.

Initially the reverse shocks is Newtonian and only a negligible amount of energy is extracted from the shell. At this stage the whole shell acts "together". Half of the shell's kinetic energy is converted to thermal energy when the collected external mass is M/, where M is the shell's mass [184, 333]. This takes place at a distance:

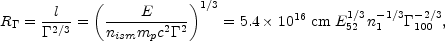(59)

where E₅₂ is the equivalent isotropic energy in 10⁵²ergs, n₁ = n_ism / 1 particle / cm³.

However, the reverse shock might become relativistic before R. Now energy extraction from the shell is efficient and one passage of the reverse shock through the shell is sufficient for complete conversion of the shell's energy to thermal energy. The energy of the shell will be extracted during a single passage of the reverse shock across the shell. Using the expression for the velocity of the reverse shock into the shell (Eq. 55) one finds that the reverse shock reaches the inner edge of the shell at R [368]:

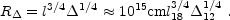(60)

The reverse shock becomes relativistic at R_N, where n₄ / n₁ = ²:

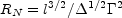(61)

Clearly, if R_N > R then the energy of the shell is dissipated while the shocks are still "Newtonain". If R_N < R the reverse shock becomes relativistic. In this case R looses its meaning as the radius where the energy is dissipated. The energy of the shell is dissipated in this "relativistic" case at r. The question which of the two conditions is relevant depends on the parameter [368]:

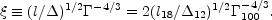(62)

I have used a canonical value for as 10¹² cm. It will be shown later that within the internal-external scenario / c corresponds to the duration of the bursts and 10¹² cm corresponds to a typical burst of 30 sec.

Using one can express the different radii as:

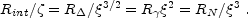(63)

For completeness I have added to this equation R_Int, where internal shocks take place (see Eq. 42). The dimensionless quantity : / . Thus:

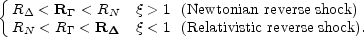(64)

I have marked in bold face the location where the effective energy extraction does take place. With typical values for l, and is around unity. The radius where energy extraction takes place is marked in bold face!

Expanding shell: A physical shell is expected to expand during as it propagates with = ₀ + R ² [315]. This will lead to a monotoneously decreasing . As the value of R is independent of it does not vary. However, R and R_N decrease from their initial values. If ₀ < R ² (corresponding to ₀ > 1) then = 1 at R = R = R_N and all three radii coincide. Given the fact that with typical parameters is of order unity this seems to be the "typical" case. The reverse shocks becomes mildly relativistic just when the energy extraction becomes efficient. However, if ₀ << 1 then the shell won't expand enough and still there will be a relativistic reverse shock operating at R. It is useful to note that in this case the effective energy extraction takes place at R for all initial values of ₀. 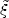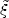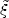In the following I denote by the value of at R: ₀ if ₀ < 1 and otherwise 1.

Overall the external shocks take place at:

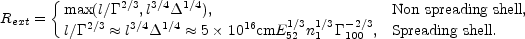(65)

Usually I will use the second relation (the spreading shell one) in the following discussion. Note that in the case of non spreading shell one uses the maximum of the two possible radii. For example in the Newtonian case where the extraction is at l / ^2/3 the shocks pass the shall many times and hence l / ^2/3 > l^{3/4 1/4}.

2. Synchrotron Spectrum from External Shocks

The bulk of the kinetic energy of the shell is converted to thermal energy via the two shocks at around the time the shell has expanded to the radius R (this would be the case in either a thick shell with < 1 or with an expanding shell that begins with ₀ > 1 but reaches 1 due to expansion of the shell around the time when R = R and efficient dissipation takes place . At this radius, the conditions at the forward shock are:

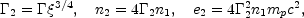(66)

while at the reverse shock:

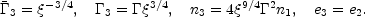(67)

Substitution of _sh = ₂ = ^3/4 in Eq. 13 yields, for the equipartition magnetic field:

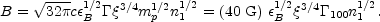(68)

If the magnetic field in region 2 behind the forward shock is obtained purely by shock compression of the ISM field, the field would be very weak, with _B << 1. Such low fields are incompatible with observations of GRBs. I consider, therefore, the possibility that there may be some kind of a turbulent instability which brings the magnetic field to approximate equipartition [108, 386]. In the case of the reverse shock, i.e. in region 3, magnetic fields of considerable strength might be present in the pre-shock shell material if the original exploding fireball was magnetic. The exact nature of magnetic field evolution during fireball expansion depends on several assumptions. Thompson [406] found that the magnetic field will remain in equipartition if it started off originally in equipartition. Mészáros, Laguna & Rees [257] on the other hand, estimated that if the magnetic field was initially in equipartition then it would be below equipartition by a factor of 10^-5 by the time the shell expands to R. It is uncertain which, if either one, of the estimates is right. As in the forward shock, an instability could boost the field back to equipartition. Thus, while both shocks may have _B << 1 with pure flux freezing, both could achieve _B 1 in the presence of instabilities. In principle, _B could be different for the two shocks. For simplicity I will consider the same value in the following discussions.

Following the discussion in Section VB, I assume that in both regions 2 and 3 the electrons have a power law distribution with a minimal Lorentz factor _e,min given by Eq. 22 with the corresponding Lorentz factors for the forward and the reverse shocks.

Forward shock: The typical energy of synchrotron photons as well as the synchrotron cooling time depend on the Lorentz factor _e of the relativistic electrons under consideration and on the strength of the magnetic field. Using Eq. 22 for _e,min and Eq. 16 for the characteristic synchrotron energy for the forward shock:

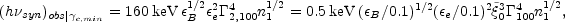(69)

and

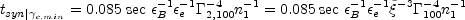(70)

The characteristic frequency and the corresponding cooling time for the "typical" electron are larger and shorter by a factor of [(p - 2) / (p - 1)]², correspondingly.

The electrons at the forward shock are fast cooling and w the typical cooling frequency is [373]:

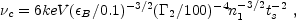(71)

where t_s is the time in seconds. The photons from the early forward shock are in the low -rays to X-ray range, but this depends strongly on the various parameters (note the strong ₂⁴ dependence in equation 69). For this set of canonical parameters _m < _c. However, the ratio of these two frequencies depends on ⁸! For slightly larger then 100 the inequality will reverse and the system will be in the fast cooling regime.

Reverse Shock: The Lorentz factor of the reverse shock, 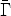₃ is smaller by a factor of ^3/2 than the Lorentz factor of the forward shock ₂. Similarly the Lorentz factor of a "typical electron" in the reverse shock is lower by a factor ^3/2 . Therefore the observed energy is lower by a factor ^{3 2}. The typical synchrotron frequency of the reverse shock is

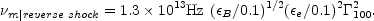(72)

This is in the IR regions but note again the strong dependence on the Lorentz factor and on _e, which could easily bring this frequency up to the optical regime. The cooling frequency in the reverse shock region is the same as the cooling frequency of the forward shock (if both regions have the same _B) [373] hence:

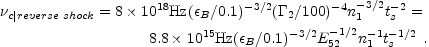(73)

In the forward shock _m is comparable or larger than _c. In the reverse shock _m < _c and it is usually in the slow cooling regime. The reverse shocks exists for a short time until it reaches the back of the relativistic shell. Then it turns into a rarefraction wave that propagates forwards. After some back and forth bounces of these wave all the matter behind the forward shock organizes itself in the form of the Blandford-McKee self similar solution discussed latter in Section VIIA. This above estimates suggest [236, 371, 372, 373] that during the short phase in which the reverse shock exists it should produce a powerful optical flash. This flash should coincide with the late part of the GRB. Kobayashi [192] calculates the light curves and typical frequencies of the reverse shock for a variety of conditions.