Gamma-Ray Bursts and the Fireball Model

6.1. A simple model

The evolution of a homogeneous fireball can be understood by a simple analogy to the Early Universe [220]. Consider, first, a pure radiation fireball. If the initial temperature is high enough pairs will form. Because of the opacity due to pairs, the radiation cannot escape. The pairs-radiation plasma behaves like a perfect fluid with an equation of state p = rho / 3. The fluid expands under of its own pressure. As it expands it cools with propto R^-1 ( being the local temperature and R the radius). The system resembles quite well a part of a Milne Universe in which gravity is ignored. As the temperature drops below the pair-production threshold the pairs annihilate. When the local temperature is around 20 keV the number of pairs becomes sufficiently small, the plasma becomes transparent and the photons escape freely to infinity. In the meantime the fireball was accelerated and it is expanding relativistically outwards. Energy conservation (as viewed from the observer frame) requires that the Lorentz factor that corresponds to this outward motion satisfies gamma propto R. The escaping photons, whose local energy (relative to the fireball's rest frame) is approx 20 keV are blue shifted. An observer at rest detects them with a temperature of _obs propto gamma . Since propto R^-1 and gamma propto R we find that the observed temperature, _obs, approximately equals ₀, the initial temperature. The observed spectrum, is however, almost thermal [217] and it is still far from the one observed in GRBs.

In addition to radiation and e⁺ e^- pairs, astrophysical fireballs may also include some baryonic matter which may be injected with the original radiation or may be present in an atmosphere surrounding the initial explosion. These baryons can influence the fireball evolution in two ways. The electrons associated with this matter increase the opacity, delaying the escape of radiation. Initially, when the local temperature is large, the opacity is dominated by e⁺ e^- pairs [217]. This opacity, tau _p, decreases exponentially with decreasing temperature, and falls to unity when = _p approx 20 keV. The matter opacity, tau _b, on the other hand decreases only as R^-2, where R is the radius of the fireball. If at the point where tau _p = 1, tau _b is still > 1, then the final transition to tau = 1 is delayed and occurs at a cooler temperature.

More importantly, the baryons are accelerated with the rest of the fireball and convert part of the radiation energy into bulk kinetic energy. The expanding fireball has two basic phases: a radiation dominated phase and a matter dominated phase. Initially, during the radiation dominated phase the fluid accelerates with gamma propto R. The fireball is roughly homogeneous in its local rest frame but due to the Lorentz contraction its width in the observer frame is Delta approx R_i, the initial size of the fireball. A transition to the matter dominated phase takes place when the fireball has a size

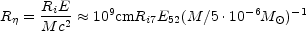(12)

and the mean Lorentz factor of the fireball is gamma approx E / M c². We have defined here E₅₂ ident E / 10⁵² ergs and R_i7 ident R_i / 10⁷ cm. After that, all the energy is in the kinetic energy of the matter, and the matter coasts asymptotically with a constant Lorentz factor.

The matter dominated phase is itself further divided into two sub-phases. At first, there is a frozen-coasting phase in which the fireball expands as a shell of fixed radial width in its own local frame, with a width ~ 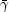bar{gamma} R_i ~ (E / M c²)R_i. Because of Lorentz contraction the shell appears to an observer with a width Delta approx R_i. Eventually, when the size of the fireball reaches R_s = Delta gamma ² approx 10¹¹ cm( Delta / 10⁷ cm)( gamma / 100)² variability in gamma within the fireball results in a spreading of the fireball which enters the coasting-expanding phase. In this final phase, the width of the shell grows linearly with the size of the shell, R:

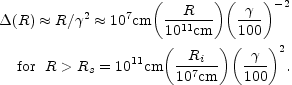(13)

The initial energy to mass ratio, eta = (E / M c²), determines the order of these transitions. There are two critical values for eta [220]:

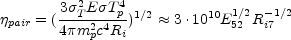(14)

and

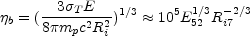(15)

These correspond to four different types of fireballs:

**Table 4.** Different Fireballs

Type	= E / M c²	M

Pure Radiation	_pair <	M < M_pair = 10^-12 M E₅₂^1/2 R_i7^1/2
Electrons Opacity	_b < < _pair	M_pair < M < M_b = 2 ^. 10^-7 M E₅₂^2/3 R_i7^2/3
Relativistic Baryons	1 < < _b	M_b < M < 5 ^. 10^-3 M E₅₂
Newtonian	< 1	5 ^. 10^-4 M E₅₂ < M

(i) A Pure Radiation Fireball (_pair < ): The effect of the baryons is negligible and the evolution is of a pure photon-lepton fireball. When the temperature reaches _p, the pair opacity _p drops to 1 and _b << 1. At this point the fireball is radiation dominated (E > M c²) and most of the energy escapes as radiation.

(ii) Electron Dominated Opacity (_b < < _pair): In the late stages, the opacity is dominated by free electrons associated with the baryons. The comoving temperature decreases far below _p before reaches unity. However, the fireball continues to be radiation dominated and most of the energy still escapes as radiation.

(iii) Relativistic Baryonic Fireball (1 < < _b): The fireball becomes matter dominated before it becomes optically thin. Most of the initial energy is converted into bulk kinetic energy of the baryons, with a final Lorentz factor _f (E / M c²). This is the most interesting situation for GRBs.

(iv) Newtonian Fireball ( < 1): This is the Newtonian regime. The rest energy exceeds the radiation energy and the expansion never becomes relativistic. This is the situation, for example in supernova explosions in which the energy is deposited into a massive envelope.