6.2. Extreme-Relativistic Scaling Laws

The above summary describes the qualitative features of a roughly homogeneous expanding fireball. Surprisingly similar scaling laws exists also for inhomogeneous fireballs [229] as well as for relativistic winds [53]. Consider a spherical fireball with an arbitrary radial distribution of radiation and matter. Under optically thick conditions the radiation and the relativistic leptons (with energy density e) and the matter (with baryon mass density ) at each radius behave like a single fluid, moving with the same velocity. The pressure, p, and the energy density, e, are related by p = e / 3. We can express the relativistic conservation equations of baryon number, energy and momentum using characteristic coordinates: r and s t - r as [229]:

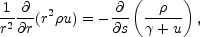(16)

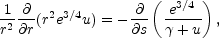(17)

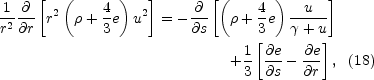(18)

where u = u^r = (² - 1)^1/2, and we use units in which c = 1 and the mass of the particles m = 1. The derivative / r now refers to constant s, i.e. is calculated along a characteristic moving outward at the speed of light. After a short acceleration phase we expect that the motion of a fluid shell will become highly relativistic ( >> 1). If we restrict our attention to the evolution of the fireball from this point on, we may treat ^-1 as a small parameter and set u, which is accurate to order O(^-2). Then, under a wide range of conditions the quantities on the right-hand sides of Eqs. 16-18 are significantly smaller than those on the left. When we neglect the right hand sides of Eqs. 16-18 the problem becomes effectively only r dependent. We obtain the following conservation laws for each fluid shell:

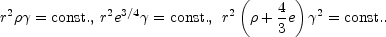(19)

A scaling solution that is valid in both the radiation-dominated and matter-dominated regimes, as well as in the transition zone in between, can be obtained by combining the conserved quantities in Eq. 19 appropriately. Let t₀ be the time and r₀ be the radius at which a fluid shell in the fireball first becomes ultra-relativistic, with few. We label various properties of the shell at this time by a subscript 0, e.g. ₀, ₀, and e₀. Defining the auxiliary quantity D, where

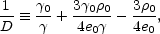(20)

we find that

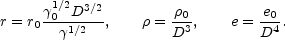(21)

These are parametric relations which give r, , and e of each fluid shell at any time in terms of the of the shell at that time. The parametric solution 21 describes both the radiation-dominated and matter-dominated phases of the fireball within the frozen pulse approximation. That is as long as the fireball does not spread due to variation in the velocity.