III. BRANE COSMOLOGY: STICKING CLOSE TO HOME

Although superstring theory promises to synthesize general relativity with the other fundamental forces of nature, it introduces a number of surprising features - such as the existence of microscopic strings, rather than particles, as the fundamental units of matter, along with the existence of several extra spatial dimensions in the universe. Could our observable universe really be built from such a bizarre collection of ingredients?

Naïvely, one might expect the extra dimensions to conflict with the observed behavior of gravity. To be successful, string theory, like general relativity, must reduce to Newton's law of gravity in the appropriate limit. In Newton's formulation, gravity can be described by force lines that always begin and end on masses. If the force lines could spread in n spatial dimensions, then at a radius r from the center, they would intersect a hypersphere with surface area proportional to r^n-1. An equal number of force lines would cross the hypersphere at each radius, which means that the density of force lines would be proportional to 1 / r^n-1. For n = 3, this reproduces the familiar Newtonian force law, F 1 / r², which has been tested (along with its Einsteinian generalization) to remarkable accuracy over a huge range of distances, from astronomical scales down to less than a millimeter [30, 31].

An early response to this difficulty was to assume that the extra spatial dimensions are curled up into tiny closed circles rather than extending to macroscopic distances. Because gravity has a natural scale, known as the Planck length, l_P [ 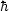G / c³]^1/2 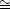10^-35 m [where 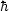is Planck's constant divided by 2], physicists assumed that l_P sets the scale for these extra dimensions. Just as the surface of a soda straw would appear one-dimensional when viewed from a large distance - even though it is really two-dimensional - our space would appear three-dimensional if the extra dimensions were "compactified" in this way. On scales much larger than the radii of the extra dimensions, r_c, we would fail to notice them: The strength of gravity would fall off in its usual 1 / r² manner for distances r >> r_c, but would fall off as 1 / r^n-1 for scales r << r_c [32]. The question remained, however, what caused this compactification, and why this special behavior affected only some but not all dimensions.

Recently Arkani-Hamed, Dimopoulos, and Dvali [33] realized that there is no necessary relation between l_P and r_c, and that experiments only require r_c 1 mm. Shortly afterward, Randall and Sundrum [34, 35] discovered that the extra dimensions could even be infinite in extent! In the Randall-Sundrum model, our observable universe lies on a membrane, or "brane" for short, of three spatial dimensions, embedded within some larger multidimensional space. The key insight is that the energy carried by the brane will sharply affect the way the gravitational field behaves. For certain spacetime configurations, the behavior of gravity along the brane can appear four-dimensional (three space and one time), even in the presence of extra dimensions. Gravitational force lines would tend to "hug" the brane, rather than spill out into the "bulk" - the spatial volume in which our brane is embedded. Along the brane, therefore, the dominant behavior of the gravitational force would still be 1 / r².

In simple models, in which the spacetime geometry along our brane is highly symmetric, such as the Minkowski spacetime of special relativity, the effective gravitational field along our brane is found to mimic the usual Einsteinian results to high accuracy [36, 37]. At very short distances there are calculable (and testable) deviations from standard gravity, and there may also be deviations for very strong gravitational fields, such as those near black holes. There are also modifications to the cosmological predictions of gravity. In the usual case, when Einstein's equations are applied to a homogeneous and isotropic spacetime, one finds H² - k / a², where k is a constant connected to the curvature of the universe. If instead we lived on a brane embedded within one large extra dimension, then H² + ² - k / a², where is a constant [38].

Under ordinary conditions, decreases as the universe expands, and so the new term in the effective Einstein equations should have minimal effects at late times in our observable universe. But we saw above that during an inflationary epoch, 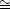constant, and in these early moments the departures from the ordinary Einsteinian case can be dramatic. In particular, the ² term would allow inflation to occur at lower energies than are usually assumed in ordinary (nonembedded) models, with potential energy functions that are less flat than are ordinarily needed to sustain inflation. Moreover, the spectrum of primordial perturbations would get driven even closer to the scale-invariant shape, with n_s = 1.00 [39, 40]. Brane cosmology thus leads to some interesting effects during the early universe, making inflation even more robust than in ordinary scenarios.