2. BASIC MHD

The evolution of the magnetic field B is governed by the induction equation

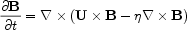(1)

got from combining Maxwell equations (neglecting the displacement current) and a simple form of Ohms law. Here U is the fluid velocity and the microscopic resistivity. The field back reacts on U via the Lorentz force J × B

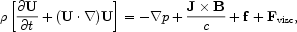(2)

where , p are the fluid density and pressure, f represents all the body forces and F_visc the viscous force. A few simple consequences of the above equations are as follows: (i) If U = 0, then the field simply decays due to finite resistivity. (ii) On the other hand for 0, the magnetic flux = _S B ⋅ dS through any surface moving with the fluid is 'frozen' in the sense that d / dt 0. (iii) The magnetic Reynolds number R_m = (UB) / ( B / L) = UL / measures the relative importance of the induction and resistive effects. (Here U and L are respectively the typical velocity and length scale in the system.) For most astrophysical systems R_m >> 1. In galaxies we expect naively R_m ~ 10¹⁸ and in clusters R_m ~ 10²⁹ based on the Spitzer resistivity [2]. Plasma instabilities in the presence of a weak magnetic field could produce fluctuating magnetic fields which scatter charge particles and affect various transport processes [3]. But to affect resistivity by scattering electrons, these fluctuations need to have significant power down to the electron gyro radius. (iv) Note that B = 0 is perfectly valid solution to the induction equation! So magnetic fields can only arise from a zero field initial condition, if the usual form of Ohm's law is violated by a "battery term" (see below), to generate a seed magnetic field B_seed. (v) The resulting seed magnetic field is generally very much smaller than observed fields in galaxies and clusters and so one needs the motions (U) to act as a dynamo and amplify the field further. It turns out to be then crucial to understand how dynamos work and saturate.

At this stage it is important to clarify the following: it is often mistakenly assumed that if one has a pre-existing magnetic field in a highly conducting medium, and the resistive decay time is longer than say a Hubble time, then one does not need any mechanism for maintaining such a field. This is not true in general; because given a tangled field the Lorentz forces would drive motions in the fluid. These would either dissipate due to viscous forces if such forces were important (at small values of the fluid Reynolds number Re = UL / , where is the fluid viscosity) or if viscosity is small, drive decaying MHD turbulence, with a cascade of energy to smaller and smaller scales and eventual dissipation on the dynamical timescales associated with the motions. This timescale can be much smaller than the age of the system. For example if clusters host a few µG magnetic fields say tangled on say l ~ 10 kpc scales, such fields could typically decay on the Alfvén crossing timescale l / V_A ~ 10⁸ yr, where we have taken a typical Alfvén velocity V_A ~ 100 km s^-1. Although the energy density in MHD turbulence decays with time as a power law, this time scale is still much shorter than the typical age of a cluster, which is thought to be several billion years. Similarly, if the fluid is already turbulent, the associated larger turbulent resistivity will can lead to the decay of large-scale fields (except perhaps in the presence of strong shear, where there may be dynamo action; see below). Therefore, one has to provide explicit explanation of the origin and persistence of cosmic magnetic fields; reference to the low Ohmic resistivity of the plasma is not sufficient if the gas is turbulent or the magnetic field is tangled. Hence even if the medium were highly conducting, in most cases, a dynamo is needed to maintain the observed magnetic field.