


One alternative to dark matter, particularly as an explanation for the non-Keplerian motions of rotating bodies, is called MOND (MOdified Newtonian Dynamics). In 1983 M. Milgrom proposed that the flat rotation curves observed in many galaxies may be explained without postulating any sort of missing mass in the universe. [86] He instead introduced an acceleration constant to modify Newton's second law, which would at small accelerations account for the radius independent nature of stellar motion.
Rather than the usual
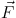 =
m
=
m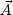 , the
equation at the heart of MOND is
, the
equation at the heart of MOND is
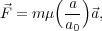 |
(30) |
 |
where 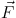 is the
force acting on an object of mass m and acceleration a =
|
is the
force acting on an object of mass m and acceleration a =
|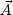 |, and
a0
|, and
a0  2 × 10-8 cm s-2 is the acceleration constant
determined by Milgrom (many other MOND theories have emerged
with differing values for a0). For accelerations greater
than or equal to a0 (most accelerations we see in
everyday life, including the motions of planets within our solar system),
x
2 × 10-8 cm s-2 is the acceleration constant
determined by Milgrom (many other MOND theories have emerged
with differing values for a0). For accelerations greater
than or equal to a0 (most accelerations we see in
everyday life, including the motions of planets within our solar system),
x  1, and
Newtonian dynamics can be used as usual.
However, for very small accelerations such as for the orbits of
objects far away from the galactic center, a0 becomes
significant; this is how MOND predicts and explains the flat
rotation curves.
1, and
Newtonian dynamics can be used as usual.
However, for very small accelerations such as for the orbits of
objects far away from the galactic center, a0 becomes
significant; this is how MOND predicts and explains the flat
rotation curves.
To demonstrate how MOND can explain flat rotation curves, we
first consider the expression for the force of gravity
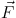 on a star and Milgrom's modification of Newton's second law:
on a star and Milgrom's modification of Newton's second law:
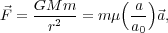 |
(31) |
where G is the gravitational constant, m and M are the masses of the star and galaxy respectively, and r is the radius of the star's orbit. If we cancel m from both sides and assume that µ (a / a0) = (a/a0) at a very large r, we are left with
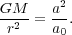 |
(32) |
Solving for a and using the relationship of acceleration with velocity and radius (a = v2 / r), we find
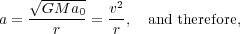 |
(33) |
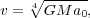 |
(34) |
where v has no dependence on r. This relation has allowed various studies to use MOND to fit flat rotation curves quite successfully for several low and high surface brightness galaxies (LSB and HSB galaxies, respectively) based on luminous mass alone. [87, 88, 89] As MOND predicts, LSB galaxies show a larger departure from Newtonian dynamics where HSB galaxies show discrepancies only in their outer regions where gravitational attraction is considerably smaller. MOND and TeVeS (the MONDian version of General Relativity) [90] have had success in predicting and describing other observed galactic dynamics as well. For a recent review, see R. H. Sanders. [91]
Despite these successes, MOND faces several major and critical challenges it has not been able to overcome. For example, when considering galaxy clusters, MOND cannot account for density and temperature profiles and requires unseen matter. [92] Evidence for dark matter exists on many distance scales and MOND essentially only works on galactic scales. Also, extremely low acceleration experiments (below a0) have been conducted, finding no departure from Newton's second law and thus constraining MOND to reduce to Newton's second law in laboratory conditions. [93, 94] And finally, gravitational lensing evidence such as in the Bullet Cluster show that, in effect, the gravitational force points back not towards regular, observed baryonic matter but rather some form of dark matter which is not observed optically. MOND theories in their current forms cannot account for such a discrepancy easily. For these reasons and others, we feel that dark matter is a more promising solution to the puzzle of missing mass in the universe.