Annu. Rev. Astron. Astrophys. 1999. 37:311-362 Copyright © 1999 by Annual Reviews. All rights reserved

4. FORMATION OF ISOLATED LOW-MASS STARS

Many low-mass stars actually form in regions of high-mass star formation, where clustered formation is the rule (Elmegreen 1985, Lada 1992, McCaughrean & Stauffer 1994). The focus here is on regions where we can isolate the individual star-forming events and these are almost inevitably forming low-mass stars.

4.1. Theoretical Issues

The theory of isolated star formation has been developed in some detail. It relies on the existence of relatively isolated regions of enhanced density that can collapse toward a single center, though processes at smaller scales may cause binaries or multiples to form. One issue then is whether isolated regions suitable for forming individual, low-mass stars are clearly identifiable. The ability to separate these from the rest of the cloud underlies the distinction between sterile and fertile parts of clouds (Section 1).

Because of the enormous compression needed, gravitational collapse plays a key role in all star formation theories. In most cases, only a part of the cloud collapses, and theories differ on how this part is distinguished from the larger cloud. Is it brought to the verge of collapse by an impulsive event, like a shock wave (Elmegreen & Lada 1977) or a collision between clouds or clumps (Loren 1976), or is the process gradual? Among gradual processes, the decay of turbulence and ambipolar diffusion are leading contenders. If the decay of turbulence leaves the cloud in a subcritical state (M < M_B), then a relatively long period of ambipolar diffusion is needed before dynamical collapse can proceed (Section 2). If the cloud is supercritical (M > M_B), then the magnetic field alone cannot stop the collapse (e.g. Mestel 1985). If turbulence does not prevent it, a rapid collapse ensues, and fragmentation is likely. Shu et al (1987a, 1987b) suggested that the subcritical case describes isolated low mass star formation, while the supercritical case describes high-mass and clustered star formation. Recently, Nakano (1998) has argued that star formation in subcritical cores via ambipolar diffusion is implausible; instead he favors dissipation of turbulence as the controlling factor. For the present section, the questions are whether there is evidence that isolated, low-mass stars form in sub-critical regions and what is the status of turbulence in these cores.

Rotation could in principle support clouds against collapse, except along the rotation axis (Field 1978). Even if rotation does not prevent the collapse, it is likely to be amplified during collapse, leading at some point to rotation speeds able to affect the collapse. In particular, rotation is usually invoked to produce binaries or multiple systems on small scales. What do we know about rotation rates on large scales and how the rotation is amplified during collapse? Is there any correlation between rotation and the formation of binaries observationally? If rotation controls whether binaries form, can we understand why collapse leads to binary formation roughly half the time? It is clear that both magnetic flux and angular momentum must be redistributed during collapse to produce stars with reasonable fields and rotation rates, and these processes will affect the formation of binaries and protoplanetary disks. Some of these questions will be addressed in the next sections on globules and cores, while others will be discussed in the context of testing specific theories.

4.2. Globules and Cores: Overall Properties

Nearby small dark clouds, or globules, are natural places to look for isolated star formation (Bok & Reilly 1947). A catalog of 248 globules (Clemens & Barvainis 1988) has provided the basis for many studies. Yun & Clemens (1990) found that 23% of the CB globules appear to contain embedded infrared sources, with spectral energy distributions typical of star forming regions (Yun 1993). About one-third of the globules with embedded sources have evidence of outflows (Yun & Clemens 1992; Henning & Launhardt 1998). Clearly, star formation does occur in isolated globules.

Within the larger dark clouds, one can identify numerous regions of high opacity (e.g. Myers et al 1983), commonly called cores (Myers 1985). Surveys of such regions in low-excitation lines of NH₃ (e.g. Benson & Myers 1989) led to the picture of an isolated core within a larger cloud, which then might pursue its course toward star formation in relative isolation from the rest of the cloud. Most intriguing was the fact that the NH₃ linewidths in many of these cores indicated that the turbulence was subsonic (Myers 1983); in some cores, thermal broadening of NH₃ lines even dominated over turbulent broadening (Myers & Benson 1983, Fuller & Myers 1993). Although later studies in other lines indicated a more complex dynamical situation (Zhou et al 1989, Butner et al 1995), the NH₃ data provided observational support for theories describing the collapse of isothermal spheres (Shu 1977). The discovery of IRAS sources in half of these cores (Beichman et al 1986) indicated that they were indeed sites of star formation. The observational and theoretical developments were synthesized into an influential paradigm for low mass star formation (Shu et al 1987a, Section 4.5).

Globules would appear to be an ideal sample for measuring sizes since the effects of the environment are minimized by their isolation, but distances are uncertain. Based on the angular size of the optical images and an assumed average distance of 600 pc (Clemens & Barvainis 1988), the mean size, ⟨ l ⟩ = 0.7 pc. A subsample of these with distance estimates were mapped in molecular lines, yielding much smaller average sizes: ⟨ l ⟩ = 0.33 ± 0.15 pc for a sample of 6 “typical” globules mapped in CS (Launhardt et al 1998); maps of the same globules in C¹⁸O J = 2 → 1 (Wang et al 1995) give sizes smaller by a factor of 2.9 ± 1.6. A sample of 11 globules in the southern sky, mapped in NH₃ (Bourke et al 1995) have ⟨ l ⟩ = 0.21 ± 0.08 pc.

Cores in nearby dark clouds have the advantage of having well-determined distances; the main issue is how clearly they stand out from the bulk of the molecular cloud. Gregersen (1998) found that some known cores are barely visible above the general cloud emission in the C¹⁸O J = 1 → 0 line. The mean size of a sample of 16 cores mapped in NH₃ is 0.15 pc, whereas CS J = 2 → 1 gives 0.27 pc, and C¹⁸O J = 1 → 0 gives 0.36 pc (Myers et al 1991). These differences may reflect the effects of opacity, chemistry, and density structure.

Globules are generally not spherical. By fitting the opaque cores with ellipses, Clemens & Barvainis (1988) found a mean aspect ratio (a / b) of 2.0. Measurements of aspect ratio in tracers of reasonably dense gas toward globules give ⟨ a / b ⟩ ∼ 1.5−2 (Wang et al 1995, Bourke et al 1995), and cores in larger clouds have ⟨ a / b ⟩ ∼ 2 (Myers et al 1991). Myers et al and Ryden (1996) have argued that the underlying 3-D shapes were more likely to be prolate, with axial ratios around 2, than oblate, where axial ratios of 3–10 were needed. However, toroids may also be able to match the data because of their central density minima (Li & Shu 1996).

The uncertainties in size are reflected directly into uncertainties in mass. For the sample of globules mapped by Bourke et al (1995) in NH₃, ⟨M_n⟩= 4 ± 1 M_⊙, compared to 10 ± 2 M_⊙ for cores. Larger masses are obtained from other tracers. For the sample of globules studied by Launhardt et al (1998), ⟨M_v⟩ = 26 ± 12 based on CS J = 2 → 1 and 10 ± 6, based on C¹⁸O J = 2 → 1. Studies of the cores in larger clouds found similar ranges and differences among tracers (e.g. Fuller 1989, Zhou et al 1994a). A series of studies of the Taurus cloud complex has provided an unbiased survey of cores with known distance identified by C¹⁸O J = 1 → 0 maps. Starting from a large-scale map of ¹³CO J = 1 → 0 (Mizuno et al 1995), Onishi et al (1996) covered 90% of the area with N > 3.5 × 10²¹ with a map of C¹⁸O J = 1 → 0 with 0.1 pc resolution. They identified 40 cores with ⟨ l ⟩ = 0.46 pc, ⟨ a / b ⟩ = 1.8, and ⟨M_n⟩= 23 M_⊙. The sizes extended over a range of a factor of 6 and masses over a factor of 80. Comparing these cores to the distribution of T Tauri stars, infrared sources, and H¹³CO⁺ emission, Onishi et al (1998) found that all cores with N > 8 × 10²¹ cm⁻² are associated with H¹³CO⁺ emission and/or cold IRAS sources. In addition, the larger cores always contained multiple objects. They concluded that the core mass per star-forming event is relatively constant at 11 M_⊙.

It is clear that characterizing globules and cores by a typical size and mass is an oversimplification. First, they come in a range of sizes that is probably just the low end of the general distribution of cloud sizes. Second, the size and mass depend strongly on the tracer and method used to measure them. If we ignore these caveats, it is probably fair to say that most of these regions have sizes measured in tracers of reasonably dense gas in the range of a few tenths of a pc and masses of less than 100 M_⊙, with more small, low mass cores than massive ones. The larger cores tend to be fragmented, so that the mass of gas with n ≥ 10⁴ cm⁻³ tends toward 10 M_⊙, within a factor of 2. Star formation may occur when the column density exceeds 8 × 10²¹ cm⁻², corresponding in this case to n ∼ 10⁴ cm⁻³.

4.3. Globules and Cores: Internal Conditions

If the sizes and masses of globules and cores are poorly defined, at least the temperatures seem well understood. Early CO observations (Dickman 1975) showed that the darker globules are cold (T_K ∼ 10 K), as expected for regions with only cosmic ray heating. Similar results were found from NH₃ (Martin & Barrett 1978, Myers & Benson 1983; Bourke et al 1995). Clemens et al (1991) showed the distribution of CO temperatures for a large sample of globules; the main peak corresponded to T_K = 8.5 K, with a small tail to higher T_K. Determination of the dust temperature was more difficult, but Keene (1981) measured T_D = 13−16 K in B133, a starless core. More recently, Ward-Thompson et al (1998) used ISO data to measure T_D = 13 K in another starless core. These results are similar to predictions for cores heated by the interstellar radiation field (Leung 1975), though T_D is expected to be lower in the deep interiors.

A sample of starless globules with A_v ∼ 1−2 mag produced no detections of NH₃ (Kane et al 1994), but surveys of H₂CO (Wang et al 1995) and CS (Launhardt et al 1998, Henning & Launhardt 1998) toward more opaque globules indicate that dense gas is present in some. The detection rate of CS J = 2 → 1 emission was much higher in globules with infrared sources. Butner et al (1995) analyzed multiple transitions of DCO⁺ in 18 low-mass cores, finding ⟨logn (cm⁻³)⟩ ≃ 5, with a tendency to slightly higher values in the cores with infrared sources. Thus, gas still denser than the ⟨logn (cm⁻³)⟩ ≃ 4 gas traced by NH₃ exists in these cores.

Discussion of the kinematics of globules and cores has often focused on the relationship between linewidth (Δ v) and size (l or R). This relation is much less clearly established for cores within a single cloud than is the relation for clouds as a whole (Section 3.3), and it may have a different origin (Myers 1985). Goodman et al (1998) have distinguished four types of linewidth-size relationships. Most studies have employed Goodman Type 1 relations (multi-tracer, multi-core), but it is difficult to distinguish different causes in such relations. Goodman Type 2 relations (single-tracer, multi-core) relations within a single cloud would reveal whether the virial masses of cores are reliable. Interestingly, the most systematic study of cores in a single cloud found no correlation in 24 cores in Taurus mapped in C¹⁸O J = 1 → 0 (γ = 0.0 ± 0.2), but the range of sizes (0.13 to 0.4 pc) may have been insufficient (Onishi et al 1996).

To study the kinematics of individual cores, the most useful relations are Goodman Types 3 (multi-tracer, single-core) and 4 (single-tracer, single-core). In these, a central position is defined, either by an infrared source or a line peak. A Type 3 relationship using NH₃, C¹⁸O J = 1 → 0 and CS J = 2 → 1 lines was explored by Fuller & Myers (1992), who found Δ v ∝ R^γ, with R the radius of the half-power contour. Caselli & Myers (1995) added ¹³CO J = 1 → 0 data and constructed a Type 1 relation for 8 starless cores, after removing the thermal broadening. The mean γ was 0.53 ± 0.07 with a correlation coefficient of 0.81. However, both these relationships depend strongly on the fact that the NH₃ lines have small Δ v and R. Some other species (e.g. HC₃N, Fuller & Myers 1993) also have narrow lines and small sizes, but DCO⁺ emission has much wider lines over a similar map size (Butner et al 1995), raising the possibility that chemical effects cause different molecules to trace different kinematic regimes within the same overall core. Goodman et al (1998) suggest that the DCO⁺ is excited in a region outside the NH₃ region and that the size of the DCO⁺ region is underestimated. On the other hand, some chemical simulations indicate that NH₃ will deplete in dense cores while ions like DCO⁺ will not (Rawlings et al 1992), suggesting the opposite solution.

A way to avoid such effects is to use a Type 4 relation, searching for a correlation between Δ v_NT as spectra are averaged in rings of larger size, though line of sight confusion cannot be avoided, as one gives up the ability to tune the density sensitivity. This method has almost never been applied to tracers of dense gas, but Goodman et al (1998) use an indirect method to obtain a Type 4 relation for three clouds in OH, C¹⁸O, and NH₃. The relations are very flat (γ = 0.1 to 0.3), and γ ≠ 0 has statistical significance only for OH, which traces the least dense gas. In particular, NH₃ shows no significant Type 4 relation, having narrow lines on every scale (see also Barranco & Goodman 1998). Goodman et al (1998) interpret these results in terms of a “transition to coherence” at the scale of 0.1–0.2 pc from the center of a dense core. Inside that radius, the turbulence becomes subsonic and no longer decreases with size (Barranco & Goodman 1998). While this picture accords nicely with the idea that cores can be distinguished from the surroundings and treated as “units” in low-mass star formation, the discrepancy between values of Δ v measured in different tracers of the dense core (cf Butner et al 1995) indicate that caution is required in interpreting the NH₃ data.

Rotation can be detected in some low-mass cores, but the ratio of rotational to gravitational energy has a typical value of 0.02 on scales of 0.1 pc (Goodman et al 1993). The inferred rotation axes are not correlated with the orientation of cloud elongation, again suggesting that rotation is not dynamically important on the scale of 0.1 pc. Ohashi et al (1997a) find evidence in several star-forming cores for a transition at r ∼ 0.03 pc, inside of which the specific angular momentum appears to be constant at about 10⁻³ km s⁻¹pc down to scales of about 200 AU.

Knowledge of the magnetic field strength in cores and globules would be extremely valuable in assessing whether they are subcritical or supercritical. Unfortunately, Zeeman measurements of these regions are extremely difficult because they must be done with emission, unless there is a chance alignment with a background radio source. Crutcher et al (1993) detected Zeeman splitting in OH in only one of 12 positions in nearby clouds. Statistical analysis of the detection and the upper limits, including the effects of random orientation of the field, led to the conclusion that the data could not falsify the hypothesis that the clouds were subcritical. Another problem is that the OH emission probes relatively low densities (n ∼ 10³ cm⁻³). Attempts to use CN to probe denser gas produced upper limits that were less than expected for subcritical clouds, but the small sample size and other uncertainties again prevented a definitive conclusion (Crutcher et al 1996). Improved sensitivity and larger samples are crucial to progress in this field. At present, no clear examples of subcritical cores have been found (Crutcher 1999a), but uncertainties are sufficient to allow this possibility.

Onishi et al (1996) found that the major axis of the cores they identified in Taurus tended to be perpendicular to the optical polarization vectors and hence B_⊥. Counterexamples are known in other regions (e.g. Vrba et al 1976) and the fact that optical polarization does not trace the dense portions of clouds (Goodman 1996) suggests that this result be treated cautiously. Further studies of B_⊥ using dust emission at long wavelengths are clearly needed.

The median ionization fraction of 23 low-mass cores is 9 × 10⁻⁸, with a range of logx_e of −7.5 to −6.5, with typical uncertainties of a factor of 0.5 in the log (Williams et al 1998). Cores with stars do not differ significantly in x_e from cores without stars, consistent with cosmic ray ionization. For a cloud with n = 10⁴ cm⁻³, the ambipolar diffusion timescale, t_AD ∼ 7 × 10⁶ yr ∼ 20 t_ff. If the cores are subcritical, they will evolve much more slowly than a free fall time. Recent comparisons of the line profiles of ionized and neutral species have been interpreted as setting an upper limit on the ion-neutral drift velocity of 0.03 km s⁻¹, consistent with that expected from ambipolar diffusion (Benson et al 1998).

To summarize the last two subsections, there is considerable evidence that distinct cores can be identified, both as isolated globules and as cores within larger clouds. While there is a substantial range of properties, scales of 0.1 pc in size and 10 M_⊙ in mass seem common. The cores are cold (T_K ∼ T_D ∼ 10 K) and contain gas with n ∼ 10⁴ cm⁻³, extending in some cases up to n ∼ 10⁵ cm⁻³. While different molecules disagree about the magnitude of the effect, these cores seem to be regions of decreased turbulence compared to the surroundings. While no clear cases of subcritical cores have been found, the hypothesis that low-mass stars form in subcritical cores cannot be ruled out observationally. How these cores form is beyond the scope of this review, but again one can imagine two distinct scenarios: ambipolar diffusion brings an initially subcritical core to a supercritical state; or dissipation of turbulence plays a similar role in a core originally supported by turbulence (Myers & Lazarian 1998). In the latter picture, cores may build up from accretion of smaller diffuse elements (Kuiper et al 1996), perhaps the structures inferred by Falgarone et al (1998).

4.4. Classification of Sources and Evolutionary Scenarios

The IRAS survey provided spectral energy distributions over a wide wavelength range for many cores (e.g. Beichman et al 1986), leading to a classification scheme for infrared sources. In the original scheme (Lada & Wilking 1984, Lada 1987), the spectral index between 2 µm and the longest observed wavelength was used to divide sources into three Classes, designated by roman numerals, with Class I indicating the most emission at long wavelengths. These classes rapidly became identified with stages in the emerging theoretical paradigm (Shu et al 1987a): Class I sources are believed to be undergoing infall with simultaneous bipolar outflow, Class II sources are typically visible T Tauri stars with disks and winds, and Class III sources have accreted or dissipated most of the material, leaving a pre-main-sequence star, possibly with planets (Adams et al 1987; Lada 1991).

More recently, submillimeter continuum observations have revealed a large number of sources with emission peaking at still longer wavelengths. Some of these new sources also have infrared sources and powerful bipolar outflows, indicating that a central object has formed; these have been designated Class 0 (André et al 1993). André & Montmerle (1994) argued that Class 0 sources represent the primary infall stage, in which there is still more circumstellar than stellar matter. Outflows appear to be most intense in the earliest stages, declining later (Bontemps et al 1996). Other cores with submillimeter emission have no IRAS sources and probably precede the formation of a central object. These were found among the “starless cores” of Benson & Myers (1989), and Ward-Thompson et al (1994) referred to them as “pre-protostellar cores.” The predestination implicit in this name has made it controversial, and I will use the less descriptive (and somewhat tongue-in-cheek) term, Class −1. There has also been some controversy over whether Class 0 sources are really distinct from Class I sources or just more extreme versions. The case for Class 0 sources as a distinct stage can be found in André et al (2000).

While classification has an honored history in astronomy, serious tests of theory are facilitated by continuous variables. Myers & Ladd (1993) suggested that we characterize the spectral energy distribution by the flux-weighted mean frequency, or more suggestively, by the temperature of a black body with the same mean frequency. The latter (T_bol) was calculated by Chen et al (1995) for many sources and the following boundary lines in T_bol were found to coincide with the traditional classes: T_bol < 70K for Class 0, 70 ≤ T_bol ≤ 650K for Class I, and 650 < T_bol ≤ 2800K for Class II. In a crude sense, T_bol captures the “coolness” of the spectral energy distribution, which is related to how opaque the dust is, but it can be affected strongly by how much mid-infrared and near-infrared emission escapes, and thus by geometry. Other measures, such as the ratio of emission at a submillimeter wavelength to the bolometric luminosity (L_smm / L_bol), may also be useful. One of the problems with all these measures is that the bulk of the energy for classes earlier than II emerges at far-infrared wavelengths, where resolution has been poor. Maps of submillimeter emission are showing that many near-infrared sources are displaced from the submillimeter peaks and may have been falsely identified as Class I sources (Motte et al 1998). Ultimately, higher spatial resolution in the far-infrared will be needed to sort out this confusion.

4.5. Detailed Theories

The recent focus on the formation of isolated, low-mass stars is at least partly due to the fact that it is more tractable theoretically than the formation of massive stars in clusters. Shu (1977) argued that collapse begins in a centrally condensed configuration and propagates outward at the sound speed (a); matter inside r_inf = at is infalling after a time t. Because the collapse in this model is self-similar, the structure can be specified at any time from a single solution. This situation is called inside-out collapse. In Shu’s picture, the pre-collapse configuration is an isothermal sphere, with n(r) ∝ r^−p and p = 2. Calculations of core formation via ambipolar diffusion gradually approach a configuration with an envelope that is close to a power law, but with a core of ever-shrinking size and mass where p∼ 0 (e.g. Mouschovias 1991). It is natural to identify the ambipolar diffusion stage with the Class −1 stage, and the inside-out collapse with Class 0 to Class I. As collapse proceeds, the material inside r_inf becomes less dense, with a power law approaching p = 1.5 in the inner regions, after a transition region where the density is not a power law. In addition, v(r) ∝ r^−0.5 at small r.

There are many other solutions to the collapse problem (Hunter 1977, Foster and Chevalier 1993) ranging from the inside-out collapse to overall collapse (Larson 1969, Penston 1969). Henriksen et al (1997) have argued that collapse begins before the isothermal sphere is established; the inner (p = 0) core undergoes a rapid collapse that they identify with Class 0 sources. They suggest that Class I sources represent the inside-out collapse phase, which appears only when the wave of infall has reached the p = 2 envelope.

Either rotation or magnetic fields will break spherical symmetry. Terebey et al (1984) added slow rotation of the original cloud at an angular velocity of Ω to the inside-out collapse picture, resulting in another characteristic radius, the point where the rotation speed equals the infall speed. A rotationally supported disk should form somewhere inside this centrifugal radius (Shu et al 1987a)

(15)

where M is the mass already in the star and disk. Since disks are implicated in all models of the ultimate source of the outflows, the formation of the disk may also signal the start of the outflow. Once material close to the rotation axis has accreted (or been blown out) all further accretion onto the star should occur through the disk.

Core formation in a magnetic field should produce a flattened structure (e.g. Fiedler & Mouschovias 1993) and Li and Shu (1996) argue that the equilibrium structure equivalent to the isothermal sphere is the isothermal toroid. Useful insights into the collapse of a magnetized cloud have resulted from calculations in spherical geometry (Safier et al 1997, Li 1998) or for thin disks (Ciolek & Königl 1998). Some calculations of collapse in two dimensions have been done (e.g. Fiedler & Mouschovias 1993). A magnetically-channeled, flattened structure may appear; this has been called a pseudo-disk (Galli & Shu 1993a, 1993b) to distinguish it from the rotationally supported disk. In this picture, material would flow into a pseudo-disk at a scale of ∼ 1000 AU before becoming rotationally supported on the scale of r_c. The breaking of spherical symmetry on scales of 1000 AU may explain some of the larger structures seen in some regions (see Mundy et al 2000 for a review).

Ultimately, theory should be able to predict the conditions that lead to binary formation, but this is not presently possible. Steps toward this goal can be seen in numerical calculations of collapse with rotation (e.g. Bonnell & Bastien 1993, Truelove et al 1998, Boss 1998). Rotation and magnetic fields have been combined in a series of calculations by Basu & Mouschovias (1995 and references therein); Basu (1998) has considered the effects of magnetic fields on the formation of rotating disks.

Theoretical models make predictions that are testable, at least in principle. In the simplest picture of the inside-out collapse of the rotationless, non-magnetic isothermal sphere, the theory predicts all the density and velocity structure with only the sound speed as a free parameter. Rotation adds Ω and magnetic fields add a reference field or equivalent as additional parameters. Departure from spherical symmetry adds the additional observational parameter of viewing angle. Consequently, observational tests have focused primarily on testing the simplest models.

4.6. Tests of Evolutionary Hypotheses and Theory

Both the empirical evolutionary sequence based on the class system and the detailed theoretical predictions can be tested by detailed observations. One can compute the expected changes in the continuum emission as a function of time for a particular model. Examples include plots of L versus A_v (Adams 1990), L versus T_bol (Myers et al 1998), and L_mm versus L (Saraceno et al 1996). For example, as time goes on, A_v decreases, T_bol increases, and L reaches a peak and declines. At present the models are somewhat idealized and simplified, and different dust opacities need to be considered. Comparison of the number of objects observed in various parts of these diagrams with those expected from lifetime considerations can provide an overall check on evolutionary scenarios and provide age estimates for objects in different classes (e.g. André et al 2000). One can also test the models against observations of particular objects. However, models of source structure constrained only by the spectral energy distribution are not unique (Butner et al 1991, Men’shchikov & Henning 1997). Observational determination of n(r) and v(r) can apply more stringent tests.

Maps of continuum emission from dust can trace the column density as a function of radius quite effectively, if the temperature distribution is known. With an assumption about geometry, this information can be related to n(r). For the Class −1 sources, with no central object, the core should be isothermal (T_D ∼ 5−10 K) or warmer on the outside if exposed to the interstellar radiation field (Leung 1975, Spencer & Leung 1978). New results from ISO will put tighter limits on possible internal energy sources (e.g. Ward-Thompson et al 1998, André et al 2000). Based on small maps of submillimeter emission, Ward-Thompson et al (1994) found that Class −1 sources were not characterized by single power laws in column density; they fit the distributions with broken power laws, indicating a shallower distribution closer to the center. This distribution appears consistent with the interpretation that these are cores still forming by ambipolar diffusion. Maps at 1.3 mm (André et al 1996, Ward-Thompson et al 1999) confirm the early results: the column density is quite constant in an inner region (r < 3000 to 4000 AU), with M ∼ 0.7 M_⊙. SCUBA maps of these sources are just becoming available, but they suggest similar conclusions (D Ward-Thompson, personal communication, Shirley et al 1998). In addition, some of the cores are filamentary and fragmented (Ward-Thompson et al 1999). Citing these observed properties, together with a statistical argument regarding lifetimes, Ward-Thompson et al (1999) now argue that ambipolar diffusion in subcritical cores does not match the data (see also André et al 2000).

For cores with central sources (Class > −1), T_D(r) will decline with radius from the source. If the emission is in the Rayleigh-Jeans limit, I_ν ∝ T_D κ(ν) N. If κ(ν) is not a function of r, I_ν(θ) ∝ ∫T_D (r) n(r) dl, where the integration is performed along the line of sight (dl). If one avoids the central beam and any outer cut-off, assumes the optically thin expression for T_D (r) ∝ r^−q, and fits a power law to I_ν(θ) ∝ θ^−m, then p = m + 1 − q (Adams 1991, Ladd et al 1991). With a proper calculation of T_D(r) and convolution with the beam, one can include all the information (Adams 1991). This technique has been applied in the far-infrared (Butner et al 1991), but it is most useful at longer wavelengths. Ladd et al (1991) found p = 1.7 ± 0.3 in two cores, assuming q = 0.4, as expected for β = 1 (equation 14). Results so far are roughly consistent with theoretical models, but results in this area from the new submillimeter cameras will explode about the time this review goes to press.

Another issue arises for cores with central objects. If a circumstellar disk contributes significantly to the emission in the central beam, it will increase the fitted value of m. Disks contribute more importantly at longer wavelengths, so the disk contribution is more important at millimeter wavelengths (e.g. Chandler et al 1995). Luckily, interferometers are available at those wavelengths, and observations with a wide range of antenna spacings can separate the contributions of a disk and envelope. Application of this technique by Looney et al (1997) to L1551 IRS5, a Class I source, reveals very complex structure (Figure 3): binary circumstellar disks (cf Rodríguez et al 1998), a circumbinary structure (perhaps a pseudo-disk), and an envelope with a density distribution consistent with a power law (p = 1.5 to 2). This technique promises to be very fruitful in tracing the flow of matter from envelope to disk. Early results indicated that disks are more prominent in more evolved (Class II) systems (Ohashi et al 1996), but compact structures are detectable in some younger systems (Terebey et al 1993). Higher resolution observations and careful analysis will be needed to distinguish envelopes, pseudo-disks, and Keplerian disks (see Mundy et al 2000 for a review). At the moment, one can only say that disks in the Class 0 stage are not significantly more massive than disks in later classes (Mundy et al 2000). Meanwhile, the interferometric data confirm the tendency of envelope mass to decrease with class number inferred from single-dish data (Mundy et al 2000).

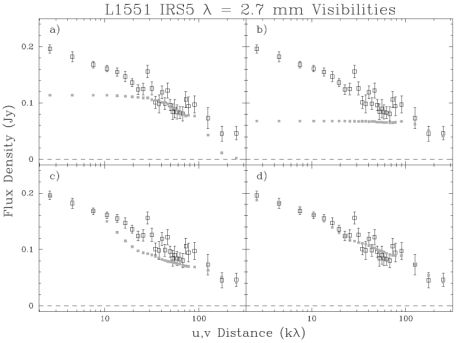Figure 3. Observed visibilities of L1551 IRS 5 at 2.7 mm, binned in annuli (open squares with error bars), are plotted versus the projected baseline in units of 103 times the wavelength. Different models are shown in each panel by the small boxes. Panel a has a model with only a Gaussian source of radius 80 AU; panel b has a model with two point sources constrained to match the map; panel c adds a truncated power law (p = 1.5, q = 0.5) envelope to the two point sources; panel d adds to the previous components a circumbinary structure, represented by a Gaussian. In the final optimization (panel d), the envelope has a mass of 0.28 M⊙ and an outer radius of 1100 AU, the circumbinary structure has a mass of 0.04 M⊙, and the circumstellar disk masses are 0.024 and 0.009 M⊙ (Looney et al 1997).

Similar techniques have been used for maps of molecular line emission. For example, ¹³CO emission has been used to trace column density in the outer regions of dark clouds. With an assumption of spherical symmetry, the results favor p ∼ 2 in most clouds (Snell 1981, Arquilla & Goldsmith 1985). The ¹³CO lines become optically thick in the inner regions; studies with higher spatial resolution in rarer isotopomers, like C¹⁸O or C¹⁷O, tend to show somewhat more shallow density distributions than expected by the standard model (Zhou et al 1994b, Wang et al 1995). Depletion in the dense, cold cores may still confuse matters (e.g. Kuiper et al 1996, Section 3.1). Addressing the question of evolution, Ladd et al (1998) used two transitions of C¹⁸O and C¹⁷O to show that N toward the central source declines with T_bol, with a power between 0.4 and 1.0. To reproduce the inferred rapid decrease in mass with time, they suggest higher early mass loss than predicted by the standard model.

By observing a series of lines of different critical density, modeling those lines with a particular cloud model and appropriate radiative transport, and predicting the emission into the beams used for the observations, one can constrain the run of density more directly. Studies using two transitions of H₂CO have again supported p = 2 ± 0.5 on relatively large scales (Loren et al 1983, Fulkerson & Clark 1984). When interferometery of H₂CO was used to improve the resolution on one core, p appeared to decrease at small r (Zhou et al 1990), in agreement with the model of Shu (1977). Much of the recent work on this topic has involved testing of detailed collapse models, including velocity fields and the complete density law, rather than a single power law, as described in the next section.

4.7. Collapse

The calculation of line profiles as a function of time (Zhou 1992) for the collapse models of Shu (1977) and Larson (1969) and Penston (1969), along with claims of collapse in a low-mass star forming region (Walker et al 1986), reinvigorated the study of protostellar collapse. Collapsing clouds will depart from the linewidth-size relation (Section 4.3), having systematically larger linewidths for a given size (Zhou 1992). Other simulations of line profiles range from a simple two-layer model (Myers et al 1996) to detailed calculations of radiative transport (Choi et al 1995, Walker et al 1994, Wiesemeyer 1997, 1999).

Zhou et al (1993) showed that several lines of CS and H₂CO observed towards B335, a globule with a Class 0 source, could be fitted very well using the exact n(r) and v(r) of the inside-out collapse model. Using a more self-consistent radiative transport code, Choi et al (1995) found slightly different best-fit parameters. Using a sound speed determined from lines away from the collapse region, the only free parameters were the time since collapse began and the abundance of each molecule. With several lines of each molecule, the problem is quite constrained (Figure 4). This work was important in gaining acceptance for the idea that collapse had finally been seen.

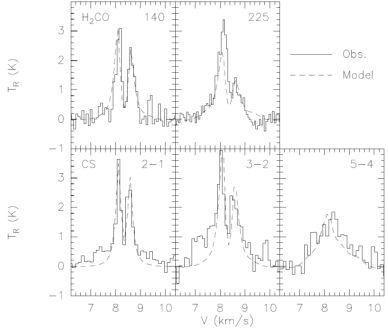Figure 4. Line profiles of H2CO and CS emission (solid histograms) toward B335 and the best-fitting model (dashed lines). The model line profiles were calculated with a Monte Carlo code, including non-LTE excitation and trapping, with an input density and velocity field taken directly from the collapse model of Shu (1977) and a temperature field calculated with a separate dust radiation transport code. The best-fitting model has an infall radius of 0.03 pc (Choi et al 1995).

Examination of the line profiles in Figure 4 reveals that most are strongly self-absorbed. Recall that the overall collapse idea of Goldreich and Kwan (1974) was designed to avoid self-absorbed profiles. The difference is that Goldreich and Kwan assumed that v(r) ∝ r, so that every velocity corresponded to a single point along the line of sight. In contrast, the inside-out collapse model predicts v(r) ∝ r^−0.5 inside a static envelope. If the line has substantial opacity in the static envelope, it will produce a narrow self-absorption at the velocity centroid of the core (Figure 5). The other striking feature of the spectra in Figure 4 is that the blue-shifted peak is stronger than the red-shifted peak. This “blue” profile occurs because the v(r) ∝ r^−0.5 velocity field has two points along any line of sight with the same Doppler shift (Figure 6). For a centrally peaked temperature and density distribution, lines with high critical densities will have higher T_ex at the point closer to the center. If the line has sufficient opacity at the relevant point in the cloud, the high T_ex point in the red peak will be obscured by the lower T_ex one, making the red peak weaker than the blue peak (Figure 6). Thus a collapsing cloud with a velocity and density gradient similar to those in the inside-out collapse model will produce blue profiles in lines with suitable excitation and opacity properties. A double-peaked profile with a stronger blue peak or a blue-skewed profile relative to an optically thin line then becomes a signature of collapse. These features were discussed by Zhou & Evans (1994) and, in a more limited context, by Snell & Loren (1977) and Leung & Brown (1977).

Figure 5. The origin of various parts of the line profile for a cloud undergoing inside-out collapse. The static envelope outside rinf produces the central self-absorption dip, the blue peak comes from the back of the cloud, and the red peak from the front of the cloud. The faster collapse near the center produces line wings, but these are usually confused by outflow wings.

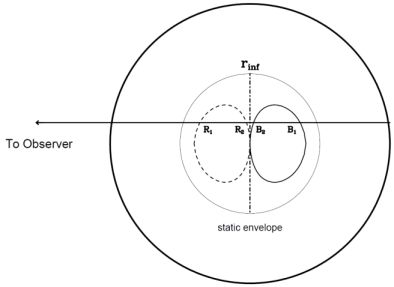Figure 6. A schematic explanation of why line profiles of optically thick, high-excitation lines are skewed to the blue in a collapsing cloud. The ovals are loci of constant line-of-sight velocity, for v(r) ∝ r−0.5. Each line of sight intersects these loci at two points. The point closer to the center will have a higher Tex, especially in lines that are hard to excite, so that Tex(R2) > Tex(R1) and Tex(B2) > Tex(B1). If the line is sufficiently opaque, the point R1 will obscure the brighter R2, but B2 lies in front of B1. The result is a profile with the blue peak stronger than the red peak (Zhou & Evans 1994).

Rotation, combined with self-absorption, can create a line profile like that of collapse (Menten et al 1987, Adelson & Leung 1988), but toward the center of rotation, the line would be symmetric (Zhou 1995). Rotating collapse can cause the line profiles to shift from blue to red-skewed on either side of the rotation axis, with the sign of the effect depending on how the rotation varies with radius (Zhou 1995). Maps of the line centroid can be used to separate rotation from collapse (Adelson & Leung 1988, Walker et al 1994).

To turn a collapse candidate into a believable case of collapse, one has to map the line profiles, account for the effects of outflows, model rotation if present, and show that a collapse model fits the line profiles. To date this has been done only for a few sources: B335 (Zhou et al 1993, Choi et al 1995), L1527 (Myers et al 1995, Zhou et al 1996, Gregersen et al 1997), and IRAS 16293 (Zhou 1995, Narayanan et al 1998). Of this group, only IRAS 16293, rotating about 20 times faster than B335, is known to be a binary (Wootten 1989, Mundy et al 1992), supporting the idea that faster rotation is more likely to produce a binary. Mathieu (1994) reviews binarity in the pre-main-sequence stage, and Mundy et al (2000) discuss recent evidence on the earlier stages.

Interferometric observations have also revealed infall motions and rotational motions on scales of ∼ 1000 AU in several sources (e.g. Ohashi et al 1997b; Momose et al 1998). Such studies can reveal how matter makes the transition from infall to a rotating disk. Inevitably, irregularities in the density and velocity fields will confuse matters in real sources, and these may be more noticeable with interferometers. Outflows are particularly troublesome (Hogerheijde et al 1998). Extreme blue/red ratios are seen in interferometric observations of HCO⁺ and HCN J = 1 → 0 lines, which are difficult to reproduce with standard models (Choi et al 1999). Even in B335, the best case for collapse, Velusamy et al (1995) found evidence for clumpy structure within the overall gradients. In addition, very high resolution observations of CS J = 5 → 4 emission toward B335 are not consistent with predicted line profiles very close to the forming star (Wilner et al 1999); either CS is highly depleted in the infalling gas, or the velocity or density fields depart from the model.

If, for the sake of argument, we accept a blue profile as a collapsing core, can we see any evolutionary trends? A number of surveys for blue profiles have been undertaken recently. Gregersen et al (1997) found 9 blue profiles in 23 Class 0 sources, using the J = 3 → 2 and J = 4 → 3 lines of HCO⁺ and H¹³CO⁺. After consideration of possible confusion by outflows, etc., they identified 6 sources as good candidates for collapse. Mardones et al (1997) extended the search to Class I sources with T_bol < 200 K, using CS and H₂CO lines. They introduced the line asymmetry as a collapse indicator:

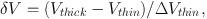(16)

where V_thick is the velocity of the peak of the opaque line, V_thin is the velocity of the peak of the optically thin line, and Δ V_thin is the linewidth of the thin line. They confirmed many of the collapse candidates found by Gregersen and identified 6 more, but they found very few collapse candidates among the Class I sources. The difference could be caused by using different tracers, since the CS and H₂CO lines are less opaque than the HCO⁺ lines. To remove this uncertainty, Gregersen (1998) surveyed the Class I sources of Mardones et al (1997) in HCO⁺. Using δ V as the measure, the fraction of blue profiles did not decrease substantially between Class 0 and Class I. Most of these line profiles need further observations before they become bona fide candidates.

When does collapse begin? Surveys of the Class −1 cores might reveal very early stages of collapse. In the inside-out collapse picture, blue profiles should appear, if at all, only toward the center. In fact, blue profiles have been seen in a substantial number of these cores (Gregersen 1998, Lee et al 1999) and maps of one, L1544, show that the blue profiles are very extended spatially (Tafalla et al 1998). Clearly, extended blue profiles in Class −1 cores do not fit expectations for early collapse, and Tafalla et al argue that the velocities are higher than expected for ambipolar diffusion. If the regions producing the blue and red peaks are indeed approaching one another, they are forming a core more rapidly than in standard models, suggesting that some new ideas may be necessary (e.g. Nakano 1998, Myers & Lazarian 1998). For a current review of this field, see Myers et al (2000).

4.8. Summary of Isolated Star Formation

Distinct cores can be identified in tracers of dense (n ≥ 10⁴ cm⁻³) gas; these cores are frequently associated with star formation. There is no clear evidence that they are magnetically subcritical, and some kinematic evidence suggests that the decay of turbulence, rather than ambipolar diffusion, is the critical feature. An empirical evolutionary sequence, based on the spectral appearance of dust emission, and detailed theoretical models are now being tested by observations. The spatial distribution of dust emission is providing important tests by probing n(r). Predictions of the evolution of spectral lines during collapse are available for the simplest theory and observations of some sources match predictions of theory quite well. Evidence of collapse is now strong in a few cases and surveys for distinctive line profiles have revealed many more possible cases.