


2.1.1. Numerical N-body methods. Gravity solvers, or N-body codes, provide the backbone for galaxy formation models, be they SAMs or hydrodynamic simulations. Fundamentally, these codes must determine the force on each mass element from all others by solving Poisson’s equation. Numerically solving Poisson’s equation to evolve large-scale structure has a long and storied history that has been extensively reviewed elsewhere (e.g. Bertschinger 1998, Bagla 2005, Dehnen & Read 2011), so we greatly limit our discussion here.
The basic approach is to subdivide a representative portion of the universe into many particles, compute the forces on these particles from all others, and evolve the system forward in discrete time-steps. In cosmological N-body simulations, the equations are solved within a comoving frame, and the volume is typically evolved with periodic boundaries, under the assumption that there are a space-filling set of identical volumes that approximately represent the larger-scale matter distribution. The expansion rate of the comoving frame is computed using the Friedmann equation (obtained from the Einstein equations within GR, see e.g. MvdBW Ch. 3.2), but the equations actually solved are the familiar Newtonian versions since GR corrections are generally negligible.
N-body methods are either particle-based, mesh-based, or a hybrid.
In galaxy formation, the most popular particle-based approach is
the tree code
(Barnes &
Hut 1986),
in which the force from distant
groups of particles are approximated via their multipole moments.
The particle-mesh (PM) method, in contrast, computes the potential
on a grid via a Fourier transform of the density field, and moves
particles along potential gradients
(Hockney
& Eastwood 1988).
Both scale with particle number N as
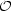 (
( log
log  ), though PM is
considerably faster. Moreover, PM codes intrinsically account for
all periodic replicas of the volume, while tree codes must use
add-on techniques such as Ewald summation
(Hernquist
et al. 1991).
), though PM is
considerably faster. Moreover, PM codes intrinsically account for
all periodic replicas of the volume, while tree codes must use
add-on techniques such as Ewald summation
(Hernquist
et al. 1991).
The advantage of tree codes is that the forces on particles can be accurately represented down to the chosen force softening length є, while PM codes are limited in resolution to their cell size. The ratio of the box length to є defines the dynamic range of the calculation. A hybrid Tree-PM approach is thus a popular method to increase dynamic range, in which the small-range forces are more accurately calculated using a tree, while large-range (and periodic) forces are computed via a faster PM method (e.g. Gadget-2; Springel 2005). The largest N-body simulations today evolve ∼ 1012 particles, with a dynamic range exceeding a million. With the advent of new computing technologies such as Graphics Processing Units, there is the potential for even larger computations if such highly-threaded, cache-limited hardware can be effectively utilized; so far this has proved challenging, but progress is being made.
2.1.2. Dark Matter Halos and Sub-halos. A basic ansatz of our current picture of galaxy formation is that galaxies form within dark matter halos. Identifying these objects in N-body simulations is the first step in constructing the merger trees (see below) that form the gravitational backbone for SAMs. On-the-fly halo finding is carried out within some hydro codes as well, in order to use halo properties for sub-grid recipes.
The halo mass (or “virial mass”) is usually defined as the mass within a sphere that encloses an average density Δvir relative to the background density of the Universe. Similarly, the virial radius is defined as the radius within which the overdensity is equal to this critical value. The actual value of Δvir is unfortunately not standardized, and is based on a simple model of the collapse of a uniform spherical overdensity. In an Einstein-de Sitter universe, after collapse and virialization, such a uniform spherical perturbation will have an average density ≃ 178 times that of the background (or critical) density (MvdBW Ch. 5.1). Many works use a fixed value of Δvir = 200, which is just a rounding up of 178; some apply it relative to the critical density and some relative to the background density. Some works use a redshift and cosmology-dependent value of Δvir, as given by the fitting function from Bryan & Norman (1998). These different conventions introduce redshift-dependent differences of as much as a factor of two in halo virial masses, radii, and internal velocities, to which readers must be alert when comparing results from the literature.
One of the generic features of the ΛCDM paradigm is that halos have a great deal of “sub-structure”. This sub-structure arises from objects that collapse and become bound at an earlier time, then get subsumed into a larger virialized structure. A “sub-halo” is a halo that was once a distinct halo but is now contained within another virialized halo.
Methods used to identify halos in N-body simulations include “friends-of-friends” (FOF), Spherical Overdensity (SO), and 6D phase-space based methods. See Knebe et al. (2011) for a comprehensive description and comparison of the results of different halo finders. Different halo finders tend to agree fairly well (within ∼ 10%) for basic halo properties such as mass and peak circular velocity of distinct halos; the cumulative z = 0 halo mass function differs by ± 10% across the 16 halo finders tested in Knebe et al. (2011). However, Klypin et al. (2011) point out that much larger differences between FOF and SO-based finders can arise at high redshift. Identifying substructure is more halo-finder dependent; here 6D phase-space based halo finders such as ROCKSTAR (Behroozi et al. 2013b) were found to perform significantly better.
2.1.3. Merger Trees. In semi-analytic models, the formation of structure through gravitational instability in an expanding Universe is represented via merger trees. A merger tree records the masses of dark matter halos and the times at which these progenitor halos merge together to form a larger halo (see Fig. 3). Merger trees may either be extracted from N-body simulations or constructed using semi-analytic methods.
The first proposed methods for constructing merger trees semi-analytically (Kauffmann et al. 1993, Cole et al. 1994, Somerville & Kolatt 1999) used statistical methods based on the Extended Press-Schechter model (Lacey & Cole 1993). More recent methods apply empirical corrections to achieve better agreement with numerical simulations (e.g. Parkinson et al. 2008). These methods provide an important complement to merger trees extracted from N-body simulations, as they are extremely flexible, and can be used to efficiently explore different cosmologies and power spectra and large dynamic ranges in halo mass. Moreover, N-body based merger trees have their own limitations, as discussed below.
Extracting merger trees from an N-body simulation appears straightforward on the face of it — one identifies dark matter halos at a series of redshifts or output times, and then identifies which halos at earlier times are “progenitors” of a given halo identified at some later time. In practice, however, there are complications. 1) Results may be sensitive to the method used for identifying halos, as discussed above. 2) The definition of progenitor is not unique, since the particles from a halo at some time t1 may end up in different halos at a later time t2. 3) A halo may be identified as a sub-halo in one timestep, then move outside of the virial radius of the host again at some later time. 4) Sub-halos are tidally stripped as they orbit within their host halos, and eventually become difficult to identify — most halo finders can no longer robustly identify sub-halos when they drop below 30-40 particles (Knebe et al. 2011).
For semi-analytic merger trees and to track sub-structure once the sub-halo can no longer be identified in the N-body simulation, most SAMs include a procedure to estimate the time for a satellite’s orbit to decay due to dynamical friction. A variation of the Chandrasekhar formula (MvdBW, Section 12.3.1) is generally used for this purpose. Many SAMs use refined versions of this formula based on numerical simulations (e.g. Boylan-Kolchin et al. 2008). Some sub-halos may be tidally destroyed before they reach the center, and their stars added to a diffuse stellar halo. Satellites that survive until they reach the center are assumed to merge with the central galaxy. SAMs then implement a set of recipes for the effect of the merger, which generally include an enhanced “burst” phase of star formation as well as some sort of morphological transformation (e.g. moving stars from the disk to the spheroid component).
2.2. Hydrodynamics: Numerical Techniques
To directly model the visible component of the Universe requires modeling gas physics, i.e. solving the equations of hydrodynamics and evolving them concurrently with the chosen gravity solver. Doing so enormously increases the complexity of the code, resulting in longer calculations with greater intrinsic uncertainties. Most hydro codes are based on solving the Euler equations (e.g. MvdBW p. 366), representing mass, momentum, and energy conservation, typically closed by assuming a non-relativistic ideal gas equation of state. The Euler equations are a form of the Navier-Stokes equations assuming no viscosity or conduction. In most cases, it is necessary to add an artificial viscosity term in order to properly handle convergent flows and shocks. Some experimentation has also been done with adding other physics whereby it is necessary to solve the Navier-Stokes equations directly; see Springel (2010b) for more discussion.
2.2.1. Lagrangian Methods. In galaxy formation, historically the most popular Lagrangian method is Smoothed Particle Hydrodynamics (SPH; see reviews by Monaghan 1992, Springel 2010b). Briefly, in SPH, the particles themselves carry the information about the fluid, which is obtained via a kernel-weighted sum over neighboring particles closer than a smoothing length (h):
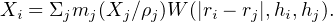 |
(1) |
Here, Xi is the quantity to be estimated, m and ρ are the particles’ mass and density, and W is the kernel, which is some spherical function of the distance between particles in units of the smoothing length. Xi can also be a gradient of a quantity, in which case the gradient propagates through to the kernel which becomes ∇ W. The efficiency and simplicity of evaluating the Euler equations based on these local kernel-smoothed quantities gives SPH many of its key advantages, including natural spatial adaptivity and trivial implementation in three dimensions.
“Classic” SPH (e.g. Hernquist & Katz 1989, Monaghan 1992) evaluates the density first as a kernel-smoothed average over nearby masses, then the thermal energy to update the pressure, then the hydrodynamic acceleration. A variant of this method is used in the code GASOLINE (Wadsley et al. 2004). A key drawback is that this method does not explicitly conserve energy and entropy in adiabatic flows in the case of variable smoothing lengths. Entropy-conserving (EC-)SPH (Springel 2005) mitigated this flaw by explicitly including variational terms in h as derived from the Lagrangian, and was formulated using entropy as the evolved variable. EC-SPH is employed in the widely-used code Gadget-2 (Springel 2005). Subsequently, it was noted that a side-effect of EC-SPH is to create an artificial pressure between cold and hot phases, resulting in a surface tension that causes for example cold clumps moving through a hot medium to be significantly more resistant to disruption than they are in grid-based codes (Agertz et al. 2007). Ironically, classic SPH performs somewhat better in this regard (at the cost of increased particle interpenetration), but all of these versions fail to realistically capture Kelvin-Helmholtz instabilities.
Several promising approaches have been developed recently to mitigate these issues. Read & Hayfield (2012) proposed SPHS, in which they showed that the error in the momentum equation in classic SPH can be reduced by using a different kernel shape with a larger number of neighbors, along with a modification of artificial viscosity to include a higher-order dissipation switch that anticipates shocks. SPHS can yield much better results for a range of surface instability tests, but the required increase in the number of SPH neighbors (442 vs. ∼ 40) slows the calculation and lowers the resolution.
A different approach was pursued by Saitoh & Makino (2013), following on Ritchie & Thomas (2001). They argued that difficulties in classic or EC-SPH arose from the requirement that the density distribution be differentiable, which is violated at contact discontinuities. They proposed a new formulation that was “density-independent” (DI-SPH), which used kernel sums to separately obtain the energy density and internal energy, from which the density is inferred. DI-SPH was shown to remove the artificial surface tension and enable improved treatment of surface instabilities (among other tests). Hopkins (2013) re-formulated DI-SPH in terms of entropy to incorporate the improved conservation properties of EC-SPH. This pressure-entropy (PE-)SPH provides much improved handling of surface instabilities versus classic SPH, with fewer numbers of neighbors than for SPHS. A modified treatment of artificial viscosity has also been widely implemented, and helps improve the performance of SPH in this regard (e.g. Hu et al. (2014)). Thanks to such improvements, current formulations of SPH can now track surface instabilities and associated phenomena to an accuracy that, not long ago, were widely regarded to be challenging for SPH.
2.2.2. Eulerian Methods. A time-honored approach to solving hydrodynamics is to discretize the fluid onto grid cells, and then compute the advection of properties across the cell boundaries. This is the basis of Eulerian approaches, which formulate the solution to the Euler equations in the fixed frame, rather than in the fluid frame as in the Lagrangian approach.
Most current cosmological Eulerian hydro codes employ a high-order Godunov scheme. Here, the Riemann problem is solved across cell faces, which yields a pressure at each cell face, thereby giving the force on the fluid across the cell. The fluid, with all its associated properties, is then advected across the cell face. If the cell is assumed to have uniform properties within it, this is called a (first-order) Godunov solver. Modern codes employ parabolic interpolation, known as the Piecewise Parabolic Method (PPM). Note that while higher order interpolation provides a more accurate solution, it requires using information from neighboring cells which effectively lowers the spatial resolution.
Given the dynamic range involved in modeling galaxy formation, a key development was the implementation of Adaptive Mesh Refinement (AMR). Here, cells satisfying some local criteria (typically based on mass) are split into sub-cells, enabling improved resolution in those regions. This effectively achieves some of Lagrangian methods’ primary advantage of being naturally adaptive in space and time. Current AMR hydro codes for galaxy formation include Enzo (Bryan et al. 2014), RAMSES (Teyssier 2010), FLASH 3, and Hydro-Adaptive Refinement Tree (H-ART; Kravtsov et al. 1997).
2.2.3. Arbitrary Lagrangian-Eulerian Methods. Optimally, one would like to unite the advantages of PPM in handling shocks and contact discontinuities with SPH’s natural adaptivivity. One approach is to use a deformable mesh, in which the mesh follows the fluid. Such arbitrary Lagrangian-Eulerian codes have historically not played a large role in astrophysics (see e.g. Pen 1998), but this has recently changed with the introduction of Arepo (Springel 2010a).
Arepo uses a Voronoi tesselation to subdivide space around particles. A Voronoi tesselation is a space-filling set of polyhedral cells where the space within a given cell is closer to one particle than any other. The Riemann problem is then solved across the cell faces in order to obtain the force on the particle. The mesh is re-generated as the particles move. In this way, Arepo is able to naturally follow the fluid like a Lagrangian code, while retaining the advantages of Godunov solvers such as excellent handling of contact discontinuities, surface instabilities, and shocks, and the lack of artificial viscosity.
2.2.4. Advantages and Disadvantages. Traditionally, Eulerian methods have enjoyed a superiority in handling strong shocks and surface instabilities, while Lagrangian methods like SPH are more adaptive and provide increased dynamic range for a given CPU expense. However, in recent times the gaps are closing in both directions. Arepo has some important advantages over both Lagrangian and Eulerian methods, particularly EC-SPH (Vogelsberger et al. 2012).
An advantage of a particle-based approach such as SPH is that the movement of mass is directly tracked. This makes it more straightforward to follow the mass as it assembles into galaxies, and to track where material ejected from galaxies ends up. It is also straightforward to implement kinetic winds, which as we will discuss below has had substantial success as a sub-grid prescription for galactic outflows. Nonetheless, in mesh codes it is possible to use tracer particles for these purposes. For instance, Arepo has implemented kinetic winds by spawning particles that are decoupled from the hydro mesh, which then later rejoin.
AMR offers the key advantange that the mesh can be refined to arbitrarily high resolution, while particle-based methods are limited in resolution by the particle mass. This allows individual systems to be examined in great detail, albeit at great computational cost. For example, Enzo merger simulations by Kim et al. (2009) and H-ART cosmological zoom simulations by Ceverino et al. (2014) both achieved a dynamic range of ≳ 106, while the most ambitious current SPH simulations can only achieve ∼ 105.
More broadly, since all modern codes generally yield similar answers in basic tests relevant to galaxy formation where the answer is approximately known, at this stage it is difficult to identify one code or methodology that is clearly superior to the others. For most properties, differences in sub-grid prescriptions yield much larger variations than differences in hydrodynamical techniques.
2.3.1. Cooling and Heating in Numerical Simulations. The key difference between baryons and dark matter in galaxy formation is that baryons can dissipate their potential energy via radiative processes. Radiative cooling and photo-ionization heating are thus implemented in essentially all codes, while radiation transport is a growing subfield with specific applications to the epoch of reionization (EoR) and line emission.
Most simulations today also include cooling from metal line emission, which dominates particularly at 105 ≲ T ≲ 107 K for typical warm-hot gas metallicities. Early works employed cooling rates assuming collisional ionization equilibrium (Sutherland & Dopita 1993), but more recent work by Wiersma et al. (2009a) better account for the photo-ionization of metals by the metagalactic radiation field.
Simulations focusing on the post-EoR universe typically account for photo-ionization heating by assuming all the gas is optically thin and in ionization equilbrium with a spatially-uniform metagalactic radiation field (e.g. Faucher-Giguère et al. 2009, Haardt & Madau 2012). During the EoR, these assumptions break down, and continuum radiative transfer is necessary in order to properly model the feedback from photo-ionization heating on galaxy growth. Two approaches are used: applying radiative transfer in post-processing to existing density distributions (Iliev et al. 2006), which is useful for evolving large volumes to study the final stages of EoR; and full radiative hydrodynamic codes that evolve the ionizing field together with the baryons, including modeling star formation to self-consistently predict the properties of the sources (Iliev et al. 2009, Pawlik & Schaye 2011, Finlator et al. 2011, Wise & Abel 2011). Given that this review focuses on the post-reionization Universe, we will not discuss this further here.
2.3.2. Cooling and Cosmological Accretion in SAMs. Most semi-analytic models implement some variant of the self-similar cooling flow model originally proposed by White & Frenk (1991) to track the thermal evolution of gas. As the gas enters the halo, it is assumed to be shock-heated to the virial temperature Tvir = 35.9 [Vvir / (km/s)]2 K, where Vvir is the halo virial velocity. One may then calculate the cooling time, which is the time it would take for the gas to radiate away all of its energy:
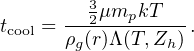 |
(2) |
Here, µmp is the mean molecular mass, T is the temperature of the gas, ρg(r) is the radial density profile of the gas, Λ(T, Zh) is the temperature and metallicity dependent cooling function (e.g. Sutherland & Dopita 1993), and Zh is the metallicity of the hot halo gas.
The hot gas is assumed to be distributed with a smooth spherically symmetric density profile. Most models assume that the density profile is described by a singular isothermal sphere (ρg(r) ∝ r−2), although some use different density profiles, such as a Navarro-Frenk-White (NFW) profile (Navarro et al. 1997) or a cored NFW profile (Cole et al. 2000).
One can then solve for the “cooling radius”, within which gas has had time to dissipate all of its thermal energy by cooling. To do this, one must adopt a timescale over which cooling is assumed to have taken place. Common choices for this timescale are the time since the halo has experienced a “major” (at least 2:1) merger (e.g. Somerville & Primack 1999), or the halo dynamical time tdyn = rvir / Vvir (e.g. Springel et al. 2001). It may happen that the model predicts rcool > rvir, indicating that the cooling time is shorter than the dynamical time, corresponding to the “cold flow” regime described in Section 1.3. In this case, most modelers generally assume that gas can flow into the halo on a dynamical time. Although this model is very simple, several studies have shown that the predicted cooling and accretion rates are in surprisingly good agreement with those from numerical hydrodynamic simulations (Benson et al. 2001, Yoshida et al. 2002, Hirschmann et al. 2012a, Monaco et al. 2014).
Tracking the enrichment of gas with heavy elements is important for cooling calculations, and for predictions of galactic chemical evolution. Most numerical hydro simulations now include a model for chemical enrichment. Early models tracked only Type II supernova (SN) enrichment, which is closely related to the oxygen abundance. To track other key elements such as carbon and iron, it is necessary to model asymptotic giant branch (AGB) stars whose ejecta dominate the present-day carbon budget, and Type Ia SN that produce the bulk of the iron in stellar-dominated systems. Such delayed feedback sources are now included in most codes, which track a suite of individual elements (Oppenheimer & Davé 2008, Wiersma et al. 2009b). The dominant uncertainty typically comes from the metal yield models from SN and stellar evolution, particularly at low metallicities and high masses. Hence at present, absolute abundance predictions should be considered accurate to only a factor of two, but relative trends of metallicity versus other galaxy properties such as stellar mass are likely more robust.
Most SAMs use a simple instantaneous recycling approximation in which a yield y of heavy elements is produced by stars in each timestep: dMZ = y dmstar, where dMZ is the mass of metals produced and dmstar is the mass of stars formed. In general these metals are deposited into the cold ISM, although some models deposit some of the metals directly in the hot halo gas. Metals may then be ejected from the cold gas reservoir by winds, and are either deposited in the IGM or in the hot gas halo. Most SAMs treat the yield y as a free parameter rather than taking it from SN yield calculations, and neglect enrichment by Type Ia SNae and AGB stars (so again, the predicted metallicities most closely trace α elements such as oxygen). However a few SAMs in recent years have incorporated more detailed treatments of chemical enrichment, tracking multiple individual elements, and the finite timescales for enrichment and gas recycling from AGB stars, Type Ia, and Type II SNae (Arrigoni et al. 2010, Nagashima et al. 2005, Yates et al. 2013).
2.5. Initial conditions and zoom simulations
The generation of standard cosmological initial conditions involves (1) generating a linear matter power spectrum via a transfer function (e.g. Eisenstein & Hu 1999); (2) Gaussian-random sampling the power spectrum for modes within the simulation volume; and (3) evolving the modes forward in the linear regime via the Zel’dovich approximation; see Bertschinger (1998) for more details. This generates particle positions and velocities sampling the matter field within a specified volume for a specified cosmology, at some specified high redshift that is optimally just before structure within the volume first goes nonlinear (see e.g. MUSIC; Hahn & Abel 2011).
An increasingly popular and useful technique is zoom simulations. In zooms, a sub-volume within a cosmologically representative region is evolved at much higher resolution, together with surrounding regions of coarser resolution that provide the tidal field from large-scale structure. After an initial coarse-grained run, a halo or region of interest is selected, and its particles are tracked back to the original initial conditions to define the zoom region. Particles within the zoom region are sampled to finer resolution, including the requisite small-scale power, and the entire volume is run again, typically with hydrodynamics turned on only in the zoom region. In this way, zooms provide an increased dynamic range at a manageable computational cost, albeit only for a single galaxy or halo and its environs.
Simulations of idealized isolated galaxies, or mergers thereof, provide a valuable testbed to explore detailed physical processes, particularly in the ISM. Initial conditions are typically created in a stable disk configuration (Hernquist 1993a), and then dynamical perturbations grow either from tides induced by a merger or internal stochasticity. Such models can achieve extremely high resolution (by cosmological standards) and can serve to isolate physics of particular interest, hence they remain useful even if they do not fully represent the cosmological baryon cycle.