

The past decade has seen remarkable progress in measuring the properties of galaxies across the electromagnetic spectrum and over the majority of cosmic history. Wide-field surveys have collected samples of millions of nearby galaxies, spanning roughly six orders of magnitude in galaxy mass and a rich range of galaxy types and environments, from isolated galaxies in voids to rich clusters. Medium-deep surveys have collected samples of tens of thousands of galaxies out to z ∼ 6, and ultra-deep surveys have identified samples of hundreds to thousands of galaxy candidates at z ∼ 6–8, with a few candidates identified (mainly behind lensing clusters) at z ∼ 9–10 (for an overview of recent surveys see Madau & Dickinson 2014). The pan-chromatic wavelength coverage enabled by a suite of ground and space based telescopes has allowed detailed Spectral Energy Distributions (SED) to be constructed for large samples of galaxies, which make it possible to estimate photometric redshifts for galaxies that are too faint to readily obtain spectroscopy, and to estimate intrinsic parameters such as stellar masses and star formation rates (SFR).
In addition, high spatial resolution imaging, primarily from the Hubble Space Telescope (HST), and spectroscopy including data from an increasing number of surveys using Integral Field Spectrographs have enabled us to study galaxies’ internal structure and kinematics. In particular, the Wide Field Camera 3 on HST has made it possible to study galaxy structure and morphology in the rest-frame optical back to “Cosmic Noon” — the peak of cosmic star formation (SF) and black hole (BH) accretion activity at z ∼ 2–3 (Madau & Dickinson 2014). We are truly living in a golden age of facilities and databases for studying how galaxies formed and evolved.
Concurrently over the past decade, advances in numerical methodologies and computing speed have allowed extraordinary progress in our ability to simulate the formation of structure within the paradigm of the Cold Dark Matter (CDM) model (e.g. Springel et al. 2005c, Klypin et al. 2011). A variety of techniques have been developed for computing detailed predictions for the expected observable properties of galaxies based on ab initio (albeit approximate) treatments of the physical processes expected to be important in shaping galaxy formation and evolution. The project of genuinely ab initio computational simulation of galaxy formation is beyond current capabilities, owing to the vast range of spatial scales involved, from the sub-pc scales of individual stars and supernovae, and accretion disks of supermassive BH, to the super-Mpc scales of the “cosmic web”, and to the wide array of poorly understood physical processes. However, by zeroing in on different scales through many different approaches, models are providing fundamental insights into the physical processes that are responsible for molding galaxy properties. Cosmological galaxy formation models have now matured into an essential tool for understanding galaxy evolution, and hence it is timely to review this topic.
We focus specifically on state-of-the-art physically-motivated cosmological models of galaxy formation, and ask a series of questions: 1) How well are these models able to predict or reproduce the observed distribution functions of global galaxy properties such as stellar mass, and the evolution of these functions? 2) How well do the models reproduce global scaling relations such as correlations between stellar mass, cold gas fraction, SFR and metallicity? 3) What do these models predict for the demographics of different types of galaxies (e.g. star forming vs. quiescent, or disk-dominated vs. spheroid-dominated)? 4) Are models able to reproduce observed structural scaling relations such as those relating mass with radial size, density, and internal velocity, and the evolution of these relations for different types of galaxies? 5) With regard to all of these questions, what insights have we gained into the process of galaxy formation from the successes and failures of our current models?
The plan for the rest of this article is as follows. In Section 1.1, we give a broad overview of the observational results that we will target in our review. In Section 1.2, we review the cosmological background, mainly pointing the reader to other sources. In Section 1.3 we give a brief overview of the physical processes that are included in most models of galaxy formation, and in Section 1.4 we introduce different tools for modeling galaxy properties. In Section 2 we give a more detailed description of the methods used in the models that we will discuss in the remainder of the article, which include numerical hydrodynamic simulations and semi-analytic models. In Section 3, we discuss the “sub-grid” modeling connected with physical processes that are not directly resolved in cosmological simulations, including the formation of stars and supermassive black holes (SMBH), and the impact of “feedback” from these objects on forming galaxies. In Section 4, we discuss the predictions of current models and how they measure up to observations for global properties of galaxies (Section 4.1) and galaxy internal structure and kinematics (Section 4.2). We conclude with a summary and outlook in Section 5. A glossary of acronyms is provided at the end of the paper.
In this review, we focus on the global and structural properties of the stellar components of galaxies from roughly Cosmic High Noon (z ∼ 2–3) to the present. We acknowledge that there are many important observations that provide crucial constraints on models that lie beyond this scope. The summary here is quite brief; we will refer the reader to other recent reviews and papers for a more comprehensive overview.
1.1.1. Global Properties: Distribution Functions. Multi-wavelength imaging surveys complemented with photometric or spectroscopic redshifts yield estimates of familiar global galaxy properties such as the luminosity and color at various rest-frame wavelengths from the UV to far-IR. In recent years, it has become popular to estimate stellar masses by fitting galaxy SEDs with simple parametric models of galaxy star formation histories combined with stellar population models (Walcher et al. 2011, Conroy 2013). Star formation rates are also estimated using SED modeling, or roughly equivalently using extinction-corrected rest-UV measures, but more reliably by adding mid- to far-IR photometry and/or nebular emission lines such as Hα. We refer to the comoving number density of galaxies as a function of a global property such as luminosity or stellar mass as a distribution function. It has long been known that galaxy distribution functions typically have a characteristic shape often described by a Schechter function (Schechter 1976), which is parameterized by a normalization, a turn-over, and an asymptotic slope to low masses. Examples of luminosity functions, stellar mass functions, and the cold gas (atomic hydrogen) mass function of nearby galaxies from recent large surveys are presented in the review by Blanton & Moustakas (2009).
To higher redshifts, galaxy rest-frame optical-NIR luminosity functions and stellar mass functions (SMF) have been measured from medium-deep surveys out to z ∼ 4. At higher redshifts, SMF estimates exist but rely on stellar mass estimates from rest-UV fluxes, which are likely less robust. These measurements have yielded a number of important insights into galaxy assembly: 1) galaxies appear to be continuously building up their mass over cosmic time, in accord with the hierarchical formation picture, and inconsistent with monolithic collapse (Madau & Dickinson 2014). 2) The number density of massive galaxies (mstar > Mchar, where mstar is the stellar mass and Mchar is the characteristic mass in the Schechter function) increases rapidly from z ∼ 4–2, but then stays nearly constant or increases slowly from z ∼ 2–0, indicating that massive galaxies formed and assembled their stars relatively early (Marchesini et al. 2009, Muzzin et al. 2013, Moustakas et al. 2013). 3) The comoving number density of low mass galaxies (mstar < Mchar) increases more rapidly than that of more massive galaxies at z ≲ 1–2, indicating that low mass galaxies formed their stars later and over a longer timescale. This result is sometimes called “mass assembly downsizing” (Cimatti et al. 2006).
It has long been known that the color-luminosity distribution of galaxies is strongly bimodal (e.g. Baldry et al. 2004), with most galaxies falling onto a relatively narrow (in optical colors) “red sequence” or a broader “blue cloud”. Spectroscopic indicators of stellar population age as well as UV and IR photometry have confirmed that in the local Universe, the “red sequence” is largely comprised of “quiescent” galaxies with predominantly old stellar populations, while the “blue cloud” represents “star forming” galaxies with younger stellar populations and significant ongoing star formation (Kauffmann et al. 2003, Brinchmann et al. 2004, Salim et al. 2007, Schiminovich et al. 2007). Because of the strongly bimodal nature of the population, it has become common to draw a line either in the color-luminosity or color-mass plane, or in the specific SFR (sSFR ≡ SFR / mstar) versus mstar plane, and to speak of “red” and “blue” galaxies or “star forming” and “quiescent” galaxies.
Recent deep surveys have shown that these two populations (star forming and quiescent) can be clearly identified at least up to z ∼ 2, and perhaps up to higher redshifts z ∼ 3–4 (Brammer et al. 2011, Muzzin et al. 2013). Intriguingly, it appears that the comoving number and mass density of quiescent galaxies has been increasing over time since z ∼ 2, while the number and mass density of star forming galaxies has stayed roughly constant or decreased during this same interval (Bell et al. 2004, Bell et al. 2007, Faber et al. 2007, Brammer et al. 2011, Muzzin et al. 2013). Given that it is the star forming population that is expected to be growing more massive due to the birth of new stars, this result has profound and unexpected implications — it implies that more and more star-forming galaxies must be having their star formation extinguished or “quenched” as cosmic time progresses.
1.1.2. Global Properties: Scaling Relations. Galaxies show many correlations between their global properties. We refer to such a correlation as a “scaling relation” when the conditional value of galaxy property y for a fixed value of another property x has a relatively small scatter. Stellar mass is often used as the x variable in galaxy scaling relations. Some well-known examples of global scaling relations with mstar are the SFR for star forming galaxies, sometimes known as the “star forming main sequence” (SFMS; Noeske et al. 2007, Wuyts et al. 2011), the mean fraction of cold gas (fgas ≡ mgas / mstar) in the interstellar medium (ISM) (Baldry et al. 2008, Peeples & Shankar 2011), and the metallicity of stars or ISM gas (mass-metallicity relation, MZR; (Gallazzi et al. 2005, Tremonti et al. 2004, Zahid et al. 2013). Furthermore, some of the tightest known scaling relations in astronomy are those between galaxy properties and the mass of the SMBH they harbor (see Kormendy & Ho 2013 for a comprehensive review).
Deep multi-wavelength surveys have provided constraints on the evolution of these scaling relations. The normalization of the SFMS has declined by a factor of ∼ 20 since z ∼ 2 (Speagle et al. 2014 and references therein), and a fairly tight sequence appears to be in place up to z ∼ 6 (Steinhardt et al. 2014, Salmon et al. 2014). The MZR seems to have evolved in the sense that galaxies of a given mass had lower gas-phase metallicities at high redshift (Savaglio et al. 2005, Erb et al. 2006, Wuyts et al. 2014, Zahid et al. 2013, Steidel et al. 2014). There is evidence from measurements of CO (an indirect tracer of molecular hydrogen, H2) in fairly massive high redshift galaxies that the gas fraction of galaxies has decreased significantly over cosmic time since z ∼ 2 (Tacconi et al. 2010, Tacconi et al. 2013, Bothwell et al. 2013b, Saintonge et al. 2013, Genzel et al. 2014). Indirect estimates of cold gas fractions from inverted star formation densities, assuming a fixed relationship between star formation density and cold gas density, also indicate a rapid decrease in cold gas fraction from z ∼ 2 to the present (Erb et al. 2006, Popping et al. 2012, Popping et al. in prep).
Some scaling relations show clear second-parameter dependences, in the sense that the scatter about a given relation is correlated with some other galaxy property. For instance, the MZR may show a second-parameter dependence on star formation, in the sense that more rapidly star forming galaxies at a given mass have lower metallicities (Mannucci et al. 2010, Lara-López et al. 2010). The cold gas content shows a similar correlation, with high H i-mass galaxies having lower metallicities (Bothwell et al. 2013a, Lara-López et al. 2013).
1.1.3. Demographics: Correlations with Galaxy Type. Since the original discovery of fuzzy “nebulae” it has been known that galaxies come in different morphological types (Hubble 1926). There are many different methods for quantifying and classifying galaxy morphology, and this subject is reviewed in Conselice (2014); see also the more nearby-Universe focussed discussion in Buta (2013). Although galaxy morphology encompasses many complex facets of galaxy structure including the presence of bulges, thin and thick disks, bars, spiral arms, etc., for the purposes of this article we focus on a single simplified metric: the fraction of a galaxy’s light or mass contributed by a flattened, rotationally supported disk, and that contained in an oblate or triaxial, pressure supported bulge or spheroid (often denoted by the bulge-to-disk ratio B / D or bulge-to-total ratio B / T). The bulge-to-disk ratio is broadly correlated with classical Hubble type (Simien & de Vaucouleurs 1986). We will further simplify much of our discussion by referring to just two classes of galaxies, “disk-dominated” and “spheroid dominated” 1. Unfortunately, there is no standard value for the critical value of B / T used to divide these populations, with values from 0.3 < (B / T)crit < 0.7 used in the literature. As it is difficult to robustly decompose the light of observed galaxies into a spheroid and disk component, other metrics such as the concentration (the ratio of the radius containing 90% of the light to the radius containing 50% of the light) or the “Sersic index” (ns; another measure of the ‘slope’ of the light profile; e.g. Blanton & Moustakas 2009) are frequently used as rough proxies for morphology. We deliberately avoid using the terms “early type” and “late type” as they are sometimes used to refer to galaxy classes divided by morphology and sometimes to those divided according to their stellar populations (star forming vs. quiescent).
Regardless of how galaxies are classified, there are robust demographic trends for disk-dominated vs. spheroid-dominated galaxies. There is a very strong trend between morphology and color or star formation activity, such that disk-dominated galaxies are predominantly blue and star forming, while spheroid-dominated galaxies are largely red and quiescent, with nearly uniformly old stellar populations (e.g. Roberts & Haynes 1994, Kauffmann et al. 2003, Blanton & Moustakas 2009). This trend appears to hold up to z ∼ 2, with the caveat that red optical color becomes a less robust tracer of old stellar populations, as many star-forming galaxies at high redshift are reddened by dust. The characteristic Schechter function mass Mchar is larger for quiescent or spheroid-dominated galaxies, and the slope is much shallower (e.g. Bernardi et al. 2010). Put another way, the fraction of spheroid-dominated galaxies increases strongly with stellar mass and luminosity. Furthermore, as emphasized by Binggeli et al. (1988), different types of galaxies can have luminosity functions that deviate considerably from the Schechter form.
A number of studies have shown that the probability for a galaxy to be quiescent depends on both its stellar mass and large-scale environment or halo mass (Balogh et al. 2004, Hogg et al. 2004, Peng et al. 2010, Woo et al. 2013). Recent works have shown that the correlation between quiescence and other internal properties such as spheroid fraction, velocity dispersion, and central density is even stronger than that with stellar mass (Bell et al. 2012, Cheung et al. 2012, Lang et al. 2014, Bluck et al. 2014).
1.1.4. Structural Scaling Relations. Both disks and spheroids exhibit correlations between their stellar mass or luminosity, their radial size, and their internal velocity (Faber & Jackson 1976, Kormendy 1977, Tully & Fisher 1977, Shen et al. 2003, Courteau et al. 2007, Bernardi et al. 2010). For disk-dominated galaxies, the radial size is usually characterized by the scale radius rs (the scale radius in the exponential function characterizing the radial light profile; e.g. Mo et al. (2010), Eqn. 2.29 p. 50) and the characteristic velocity is the rotation velocity at the maximum of the rotation curve Vrot, which usually occurs at around 2rs. For spheroid-dominated galaxies, the radial size is characterized by the half light radius or effective radius re (the radius that contains half of the total luminosity), and the internal velocity is characterized by the (line of sight) velocity dispersion σ. Several of these relationships have names, such as the Tully-Fisher relation for disks (L - Vrot; Tully & Fisher 1977), and the Faber-Jackson (L - σ; Faber & Jackson 1976), and Kormendy (L - re; Kormendy 1977) relations for spheroids. A combination of these three quantities forms a Fundamental Plane; i.e., galaxies populate a relatively thin plane in L-r-V space, or rescaled versions of these variables (Djorgovski & Davis 1987, Faber et al. 1987, Bender et al. 1992, Burstein et al. 1997). The familiar named bivariate relations are projections of this plane.
The slope, scatter, and evolution of these structural scaling relationships for spheroids and disks carry important clues about the formation history and relationship between these objects. For example, 1) the size-mass relationship is considerably steeper for spheroids than for disks at all redshifts (Shen et al. 2003, Bernardi et al. 2010, van der Wel et al. 2014); 2) since z ∼ 2, the size-mass relation for spheroids has evolved much more rapidly than that for disks (Trujillo et al. 2006, van der Wel et al. 2014); 3) the size distribution at fixed mass is narrower for spheroids than for disks (van der Wel et al. 2014) 4) the evolution of the Tully-Fisher and Faber-Jackson relation has been relatively mild (Kassin et al. 2007, Miller et al. 2011, Miller et al. 2012, Cappellari et al. 2009, Cenarro & Trujillo 2009). We note that many high redshift studies present the scaling relations for galaxies divided according to whether they are star forming or quiescent, rather than spheroid or disk dominated, but this seems to make little difference to the qualitative results (van der Wel et al. 2014).
Another illustration of the importance of structural-kinematic scaling relations is demonstrated by the distinction between “classical” bulges and “pseudo”-bulges (Kormendy & Kennicutt 2004, Kormendy 2013b). Classical bulges have centrally concentrated light profiles with Sersic indices ns ∼ 2–3 (where a de Vaucouleur profile has ns = 4), and lie on an extension of the Fundamental Plane for giant ellipticals. Pseudobulges have more extended light profiles that are more similar to disks (ns ∼ 1) and lie on a different Fundamental Plane from classical bulges and giant ellipticals (Kormendy et al. 2009). Furthermore, classical bulges and pseudobulges have different correlations with SMBH mass (Kormendy & Ho 2013). Similarly, the dwarf galaxies that are confusingly termed “dwarf spheroidals” and “dwarf ellipticals” obey very different Fundamental Plane relations than do classical bulges and ellipticals of all luminosities (Kormendy et al. 2009, Kormendy & Bender 2012). In fact, dwarf spheroidals and dwarf ellipticals are indistinguishable from dwarf irregulars in their structural parameter correlations. These diverse scaling relations hint at different formation mechanisms for these objects, as reviewed in Kormendy (2013).
Our modern theory of cosmology is based on the ansatz that the Universe is homogeneous and isotropic on large scales (the cosmological principle), and Einstein’s theory of General Relativity (GR) that says that the structure of space-time is determined by the mass and energy content of the Universe. Together these allow us to derive equations that describe the evolution of the scale factor (or characteristic size and density) of the Universe in terms of the parameters specifying the mass and energy density. Observations have shown that the Universe started from a much denser, hotter, and nearly homogeneous state and has been expanding for approximately the past thirteen and a half billion years (Mo et al. 2010, hereafter MvdBW).
In this standard picture, quantum fluctuations in the very early Universe were processed during a period of very rapid expansion called inflation to create the small inhomogeneities that are detected via temperature fluctuations in the Cosmic Microwave Background. These tiny fluctuations, viewed at the time when free electrons combined with nuclei to form neutral atoms at a redshift z ≃ 1100, have now been studied in exquisite detail with a large number of experiments, including the Wilkinson Microwave Anisotropy Probe and Planck satellites. When combined with other observations such as the distance-redshift relation from Type Ia supernovae, abundances of galaxy clusters, constraints on the present-day expansion rate (Hubble parameter H0) from nearby Cepheid stars, and galaxy clustering (e.g. Baryon Acoustic Oscillations), these measurements yield stringent constraints on the fundamental cosmological parameters (Hinshaw et al. 2013, Planck Collaboration et al. 2013).
These combined observations point to a Universe that is geometrically flat and dominated by Dark Matter and Dark Energy, which together account for more than 95% of the energy density of the Universe. The physical nature of both of these mysterious substances is unknown, although there are numerous candidates. In the most popular variant of the standard model, which we will refer to as ΛCDM, the dark matter is “cold” and collisionless and makes up ∼ 25% of the cosmic mass-energy density, and the dark energy is in the form of a “cosmological constant” Λ (as expected in the most general form of Einstein’s equations of General Relativity), comprising ∼ 70%. The remaining 4% is in baryons (which in this context include leptons), i.e. normal atoms that make up stars, gas, and heavy elements (“metals”). Although these cosmological parameters are still uncertain by up to perhaps ten percent, for the purposes of understanding how galaxies form and evolve, this level of uncertainty is largely irrelevant.
With the initial conditions specified, if we neglect “baryonic” physics, it is relatively straightforward to compute how the density field of the dominant dark matter component evolves as the Universe expands. If we imagine the matter density field as a mountain range, the landscape in the CDM picture is extremely craggy, with many small scale peaks superimposed on top of the medium and large scale peaks and valleys. As the Universe expands, the background density decreases. When a peak exceeds a critical over-density relative to the background, the region within that peak stops expanding and becomes gravitationally self-bound. Numerical N-body techniques have been used to extensively study and characterize the growth of structure in dissipationless (dark matter only) ΛCDM simulations, as we discuss in Section 2.1.1. The gravitationally bound structures that form in these simulations are commonly referred to as dark matter halos, and the abundance, internal structure, shape, clustering, and angular momentum of these halos over cosmic time has been thoroughly quantified (see MvdBW Ch. 6 and 7 and references therein). Based on these dark matter (DM) only simulations, the standard ΛCDM paradigm has been judged to be extremely successful at explaining and reproducing observations on scales larger than a few kpc (e.g. Primack 2005), thereby providing a robust framework upon which to build models of galaxy formation and evolution.
1.3. Overview of Physical Processes
In this section we briefly overview the main physical processes that are commonly included in current models of galaxy formation. We discuss these processes and their implementation in more detail in Section 2 and Section 3.
• Gravity – Gravity plays a crucial role in building the “skeleton” for galaxy formation. The shape and amplitude of the primordial power spectrum of density fluctuations depends on the cosmological parameters and the properties of dark matter. This spectrum, processed by gravity, determines the number of dark matter halos of a given mass that have collapsed at any given time, and how quickly these halos grow over cosmic time via merging and accretion. It also determines how dark matter halos cluster in space. In the standard paradigm, every galaxy is born within one of these dark halos. When halos merge, each containing their own “central” galaxy, gravity and dynamical friction gradually cause the orbits to decay, until the galaxies merge. Mergers can have important effects on galaxies, including triggering bursts of star formation and accretion onto central supermassive black holes, and transforming galaxy structure and morphology.
• Hydrodynamics and Thermal evolution – When an over-dense region composed of gas and dark matter collapses, strong shocks form, increasing the entropy of the gas. The subsequent evolution of the gas is then determined by how efficiently the gas can cool and radiate away its thermal energy. The primary cooling processes relevant for galaxy formation over most of cosmic history are two-body radiative processes. Gas that is hotter than T ≳ 107 K is fully collisionally ionized and cools predominantly via bremsstrahlung (free-free emission). In the temperature range 104 < T < 107 K, collisionally ionized atoms can decay to their ground state, and electrons can recombine with ions. Below temperatures of 104 K, cooling occurs through collisional excitation/de-excitation of heavy elements (metal line cooling) and molecular cooling.
Following collapse and shock-heating, if radiative cooling is inefficient, a pressure-supported quasi-hydrostatic gaseous halo may form. This gas will then gradually cool in what is often referred to as a cooling flow. This is also sometimes referred to as “hot mode” accretion. Once the gas cools and loses pressure support, it will collapse until it is supported by its angular momentum. If the cooling time of the gas is short compared to the dynamical time, the gas may accrete directly onto the proto-galaxy without ever forming a hot quasi-hydrostatic halo (White & Frenk 1991, Birnboim & Dekel 2003). Cosmological hydrodynamic simulations have shown that this sort of “cold mode” accretion tends to occur when gas flows in along relatively cold, dense filaments (Kereš et al. 2005).
• Star formation – Once gas has collapsed into the central regions of the halo, it may become self-gravitating, i.e. dominated by its own gravity rather than that of the dark matter. As gas cools more rapidly the higher its density, if cooling processes dominate over heating, then a run-away process can ensue whereby Giant Molecular Cloud (GMC) complexes form, and eventually some dense cloud cores within these complexes collapse and reach the extreme densities necessary to ignite nuclear fusion. However, many details of this process remain poorly understood. Moreover, most cosmological simulations are not able to resolve even the scales on which GMC form, much less individual cores. Therefore all existing cosmological simulations implement empirical sub-grid recipes to model star formation.
• Black Hole Formation and Growth – The first “seed” BH may have formed in the early universe either as the remnants of Population III (metal free) stars, via direct collapse of very low angular momentum gas, or via stellar dynamical processes (Volonteri 2010). These seed BH may grow by accreting gas that either has negligible angular momentum, or by forming an accretion disk that drains the gas of angular momentum via viscosity (Netzer 2013). These processes are, again, poorly understood and virtually impossible to model explicitly in cosmological simulations, so are modeled via sub-grid recipes.
• Star Formation Feedback – Observations show that less than 10% of the global baryon budget today is in the form of stars. However, in CDM models without some sort of “feedback” (or suppression of cooling and star formation), we would expect most of the gas to have cooled and formed stars by the present day. Even the pioneers of the earliest models of galaxy formation within a CDM framework recognized this “overcooling problem”, and suggested that energy generated by supernova explosions could heat gas and perhaps blow it out of galaxies, making star formation inefficient (White & Rees 1978, White & Frenk 1991, Dekel & Silk 1986). It is now recognized that there are many processes associated with massive stars and supernovae (e.g. photo-heating, photo-ionization, winds) that could contribute to making star formation inefficient and to driving large-scale winds that reduce the baryon fractions in galaxies (see Hopkins et al. 2012b, for an overview). Once again, most cosmological simulations cannot resolve these physical processes in detail, so nearly all current models implement sub-grid recipes to attempt to capture their effect on galaxy scales.
• AGN Feedback – There is strong observational evidence that most or perhaps all spheroid-dominated galaxies (which comprise the majority of all massive galaxies) contain a supermassive black hole (see (Kormendy & Ho 2013, for a recent review). A simple calculation indicates that the amount of energy that must have been released in growing these black holes must exceed the binding energy of the host galaxy, suggesting that it could have a very significant effect on galaxy formation (Silk & Rees 1998), however, it is still uncertain how efficiently this energy can couple to the gas in and around galaxies. Observational signatures of feedback associated with Active Galactic Nuclei (AGN) include high-velocity winds, which may be ejecting the cold ISM from galaxies, and hot bubbles apparently generated by giant radio jets, which may be heating the hot halo gas (see Fabian 2012, Heckman & Best 2014, for recent reviews). AGN feedback is also treated with sub-grid recipes in current cosmological simulations.
• Stellar populations and chemical evolution – In order to make direct comparisons between models and observations, many modelers convolve their predicted star formation histories with simple stellar population models, which provide the UV-Near IR SED for stellar populations of a single age and metallicity (Conroy 2013), folding in an assumed stellar Initial Mass Function (IMF) 2. Many models now include the important contribution of gas recycling from stellar mass loss self-consistently within simulations (Leitner & Kravtsov 2011). In addition, as stars evolve and go supernova, they produce and distribute heavy elements throughout the gas that surrounds galaxies, evidently polluting the intergalactic medium (IGM) out to fairly large distances from galaxies. Chemical evolution is a critical part of galaxy formation for several reasons: (i) cooling rates at intermediate temperatures are highly enhanced in metal-enriched gas; (ii) the luminosity and color of stellar populations of a given age are sensitive to metallicity; and (iii) heavy elements produce dust, which dims and reddens galaxies in the UV and optical and re-radiates the absorbed energy in the mid-to-far IR. Most cosmological models of galaxy formation now include a treatment of chemical evolution.
• Radiative Transfer – The radiation emitted by stars and AGN can have an important impact on galaxy formation. Radiation can directly heat gas, and can also modify cooling rates (especially for metal-enriched gas) by changing the ionization state of the gas. Moreover, the transmission of radiation of different wavelengths through and scattering by dust can greatly impact the measured total luminosity, color, and observationally determined morphological and structural properties of galaxies, especially in the rest-frame UV and optical, which are often all that is available at high redshift. Most current cosmological simulations that are run to low redshift (z ≲ 6) do not include radiative transfer self-consistently due to the added computational expense. However, with sufficiently high resolution, radiative transfer through a dusty ISM can be computed in post-processing to estimate the observed pan-chromatic properties of galaxies (e.g. Jonsson et al. 2010) and their line emission (e.g. Narayanan et al. 2008).
Theorists have developed a wide range of different tools for modeling galaxy formation and evolution. Here we briefly summarize the most commonly used tools and highlight some significant differences between them. We provide a more detailed description of the methods used in the modeling tools that are the subject of this review in Section 2.
There is a popular class of what are generally called “models”, including Halo Occupation Distribution (HOD) models (e.g., Berlind & Weinberg 2002, Zheng et al. 2005), Conditional Luminosity Function models (van den Bosch et al. 2007), and sub-halo abundance matching (SHAM) models and related techniques (e.g., Conroy et al. 2006, Tasitsiomi et al. 2004, Moster et al. 2010b, Behroozi et al. 2010). These techniques derive mappings between observable properties of galaxies and predicted properties of dark matter halos, and in general contain no actual modeling of physical processes. Although this family of techniques is extremely useful for gaining insights into the required connection between observable galaxies and dark matter halos, we will not discuss these types of “models” in detail in this review.
The most explicit way to model galaxy formation is using numerical hydrodynamic techniques, in which the equations of gravity, hydrodynamics, and thermodynamics are concurrently solved for particles and/or grid cells representing dark matter, gas, and stars. The advantage of these techniques is that, within the limitations of the adopted numerical resolution, one obtains predictions of the density of each of these three components (as well as that of heavy elements) over cosmic time. One also obtains predictions for the velocities of the stars and dark matter, and the temperature of the gas. Thus the structure and kinematics of galaxies as well as their global properties and spatial distribution can be studied in great detail (see Fig. 1 and 2 for examples). The main limitation of these techniques is that computational exigencies restrict the dynamic range that can be explicitly simulated. This, combined with our still imperfect understanding of the physics that governs “small-scale” processes such as star formation, black hole growth, and feedback processes, means that (as already discussed), many important processes must be treated using uncertain and somewhat arbitrary sub-grid recipes. Moreover, computational limitations have historically made it difficult to experiment extensively with different sub-grid recipes or to explore the multi-dimensional space of the variables that parameterize these recipes.
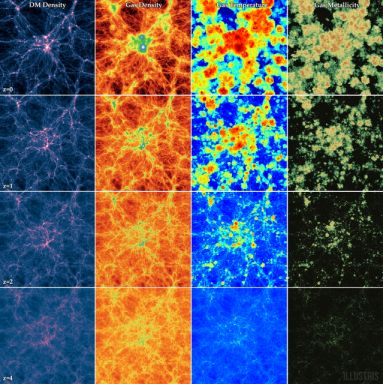 |
Figure 1. Visualization of representative quantities computed by numerical hydrodynamic simulations, from the Illustris project. From left to right, the dark-matter density, gas density, gas temperature, and gas metallicity are shown at different cosmic times (from top to bottom: z = 0, z = 1, z = 2, z = 4). The slice shown has a projected thickness of 21.3 cMpc and shows the whole Illustris simulation box which is 106.5 cMpc on a side. Reproduced from Vogelsberger et al. (2014a). |
 |
Figure 2. A 100 × 100 × 20 cMpc slice through the EAGLE simulation, illustrating the dynamic range that is attainable with state-of-the-art numerical hydrodynamic simulations. The intensity represents the gas density while the color indicates the gas temperatures (blue through green through red from cooler to hotter). The inset shows a region 10 cMpc and 60 ckpc on a side. The zoom in to an individual galaxy with stellar mass 3 × 1010 M⊙ shows the optical band stellar light. Reproduced from Schaye et al. (2014). |
The other technique that has been widely used to model galaxy formation in a cosmological context is known as “semi-analytic modeling” (SAM). This method does not explicitly solve fundamental equations for particles or grid cells, but rather adopts a set of simplified flow equations for bulk components (see Baugh 2006, Benson 2010, for reviews). For example, a typical SAM tracks how much gas accretes into halos, how much hot gas cools and turns into stars, how feedback processes remove cold gas from the galaxy or heat the halo gas, how mergers transform disks into spheroids, etc. Fig. 3 shows graphical representations of some of the quantities that can be tracked in a SAM for several example halo “merger trees”.
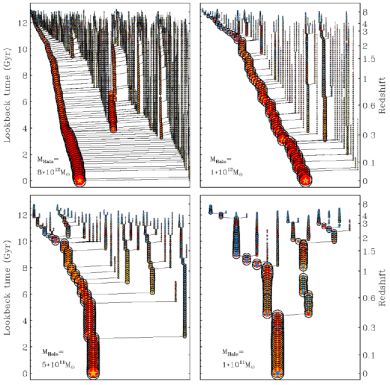 |
Figure 3. Visualization of representative predictions from a semi-analytic model. Symbol sizes represent the mass of the host dark matter halo; the x-axis is arbitrary. Symbols connected by lines represent halo mergers. Colors represent the mass of different galaxy components (red: hot gas; blue: cold gas; yellow: stars). Several different final host halo masses are shown as indicated on the figure panels. Halos with the same virial mass can have a diversity of merger histories (not shown). Reproduced from Hirschmann et al. (2012a). |
The computational requirements of these models are enormously reduced compared with fully numerical simulations. This makes it possible to make predictions for very large volumes, or to simulate galaxies over a larger range of halo mass, and also to extensively explore different sub-grid recipes treating the most uncertain aspects of galaxy formation. Recently, several groups have coupled SAMs with a Bayesian inference approach, and used Markov Chain Monte Carlo techniques to sample the posterior probability distribution of the multi-dimensional space of the model parameters (Henriques et al. 2009, Lu et al. 2011). This is a powerful approach for exploring parameter degeneracies and obtaining more rigorous statistical assessments of the “goodness of fit” of specific models or model families with observational data (see Bower et al. 2010) for an alternative approach using Bayesian Emulator methods). As well, the less explicit nature of SAMs has allowed modelers to bypass some of the numerical issues which for many years caused difficulties in reproducing basic properties of galaxies in numerical simulations.
The field has now reached an interesting point where numerical simulations have started to be able to reproduce fundamental observations at a similar level as semi-analytic models. Interestingly, much of this success has been achieved by adopting a similar approach to the one that has long been used by SAMs, namely, 1) parameterizing the physical processes that can’t be simulated explicitly, and tuning these parameters to match a subset of observations, 2) experimenting with different sub-grid recipes to achieve the best match to a set of observations. Even the recipes themselves are in many cases very similar to the ones that are commonly implemented in SAMs. Encouragingly, the two techniques have arrived at the same qualitative conclusions about galaxy formation and evolution for all of the topics that we will discuss in this article. For this reason, we structure this article largely in terms of the physical processes and general insights into how they shape galaxy formation, giving examples from both SAMs and numerical simulations.
1 In this paper we use the term “spheroid” to mean galaxies or galaxy components that structurally and kinematically resemble classical giant ellipticals, not to be confused with “dwarf spheroidals” or “spheroidal galaxies”. See Section 1.1.4 for further explanation. Back.
2 Note that all cosmological simulations to date, as far as we are aware, have assumed that the IMF is universal. However, there is mounting evidence that this assumption may not be valid (see the recent review by Bastian, Covey & Meyer 2010), which could have important implications for galaxy formation. Back.