


Cosmology is the study of the universe in its entirety. Large-scale galaxy surveys suggest that the universe follows the Cosmological Principle, stating the properties of the universe are the same for all observers when viewed at large enough scales (greater than 300 Mpc) 3 In other words, the large-scale structure of the universe would be indistinguishable when traveling through space. At these scales, the universe is said to be isotropic and homogeneous. An isotropic universe means that there is no special direction in the universe, that is, it looks the same in all directions. A homogeneous universe is one with constant density and the distribution of galaxies is the same wherever the observer looks.
An isotropic and homogeneous universe can be treated as one entity. One can use general relativity to describe its dynamics, starting with the FLRW 4 space-time metric,
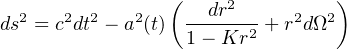 |
(1) |
which results in an equation of motion describing its expansion or contraction. Here ds, dt, and dΩ are intervals of space-time, time, and angle, respectively, and c is the speed of light. The variable r is a spherical coordinate describing some observer and is not necessarily a distance measure between two observers. The curvature K is a constant and can be either –1, 0, or +1, respectively corresponding to negative (elliptical), flat (Euclidean), and positive (hyperbolic) curvature of space.
The scale factor a(t) denotes the expansion of the universe, where it is convention to take a = 1 at the present day. In other words, when the universe had only expanded to half of its current size, a = 1/2. The scale factor is also related to cosmological redshift z = 1/a − 1, which is common measure of distance and time in cosmology. A solution to the FLRW metric is the Friedmann equation
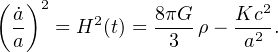 |
(2) |
Here H(t) is the Hubble parameter that describes the expansion (positive) or contraction (negative) rate of the universe. Edwin Hubble first discovered the expansion of the universe in 1927 by determining that more distant galaxies were receding at faster velocities. The present day value H0 is thus usually given in units of km s−1 Mpc−1 that is the slope of this relationship.
The total mass-energy density ρ = ρm + ρr + ρΛ of the universe comprises
It is useful to define the critical density ρc = 3H02 / 8π G, which is obtained by solving for ρ in Equation 2 after setting K = 0. It is the dividing line between an open universe that expands forever and a closed universe that collapses onto itself.
Current constraints on the mass-energy components come from several experiments and sources — cosmic microwave background, supernovae, galaxy clusters, and large-scale structure. They have shown that the universe is flat (K = 0), and about 69%, 26%, and 5% of the mass-energy is contained in dark energy, cold dark matter (DM), and baryons, respectively [13]. A small fraction (9.3 × 10−5) is contained in radiation. These percentages of the i-th mass-energy component are always given in units of the critical density as Ωi ≡ ρi / ρc: (ΩΛ, Ωc, Ωb, Ωr) ≃ (0.69, 0.26, 0.05, 9.3 × 10−5). Unless otherwise stated, we assume these cosmological parameters in this article.
The Friedmann equation can be integrated to find that the scale factor a or (1 + z)−1 is proportional to t1/2 in a radiation-dominated universe, t2/3 in a flat matter-dominated (the so-called Einstein-de Sitter, EdS) universe, and expands exponentially in a vacuum-dominated universe. The latest observational constraints suggest that the universe is flat and the cosmological constant exists (ρΛ > 0), thus the scale factor a(t) is monotonically increases with time, i.e. the universe is expanding and accelerating.
Knowing how the universe expands as a function of time, we also know how the mean temperature of the universe behaves, assuming it is filled with a perfect fluid. Starting from a hot Big Bang, the universe undergoes several phase transitions, where some are associated with the splitting of the four fundamental forces – gravity, strong, weak, and electromagnetic. All large-scale structures are seeded by quantum fluctuations that exponentially grew in size during the inflationary epoch (t ∼ 10−36 − 10−32 s after the Big Bang) that eventually evolve into galaxies, shown in the cosmic timeline in Figure 1.
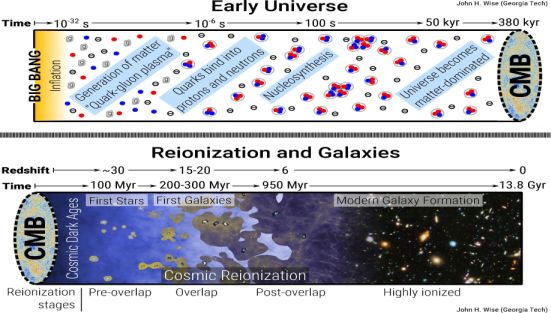 |
Figure 1. Cosmic timeline of the universe before (top) and after (bottom) recombination along with the stages of reionization. The galaxy survey image is taken from the Hubble Ultra Deep Field. |
Along the way, one landmark cosmic event in the Universe occurred when gas transitioned from an ionized to a neutral state, known as either recombination or the surface of last scattering. Because the density of free electrons suddenly decreases, the photons become decoupled from matter and stream away, creating the cosmic microwave background (CMB).
After photons decouple, the universe at this time is a very dark and lonely place before stars or galaxies have formed. This epoch is sometimes referred to as the ’Dark Ages’ [14]. From this starless, neutral, and cold state, the entire universe will be gradually reionized by nascent galaxies and their constituents.
On small scales, the universe is neither isotropic nor homogeneous. One can look at our Milky Way and other galaxies just to see the inhomogeneity of matter. In the absence of light pollution, the dense stellar fields of the Milky Way, intertwined with dark dust lanes, stretch from horizon to horizon. Our galaxy is a very clumpy and active region in the universe, scattered with stellar clusters, cold molecular clouds, warm ionized regions, and hot supernova remnants.
On slightly larger scales, these ’island universes’ congregate in groups and clusters, containing dozens and hundreds of galaxies, respectively, which are connected to each other through long filaments. These cosmic connections form the cosmic web (see Figure 2) containing all cosmic structure: groups, clusters, superclusters, filaments, walls, and voids. When viewed in hundreds of Mpc, galaxy number densities become uniform, and web seems to repeat itself, suggesting the Cosmological Principle holds.
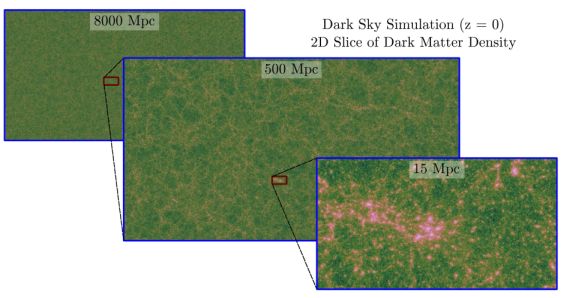 |
Figure 2. The Cosmic Web shown through slices of dark matter density in the Dark Sky Simulations [15] at the present-day. The fields of view in the left, center, and right panels are 8000, 500, and 15 Mpc. The universe is homogeneous and isotropic at scales above 300 Mpc but below which forms large-scale structures (clusters, filaments, walls, and voids). |
The cold dark matter (CDM) paradigm [16, 17, 18] explains cosmological large-scale structure extremely well, predicting galaxy number densities and their clustering to great accuracy. Because DM constitutes most of the matter in the universe, it controls the dynamics of large-scale structure. In any CDM cosmology, the building blocks are DM halos that have gravitationally collapsed and decoupled from the expansion of the universe. When a halo collapses, the dark matter and gas reaches equilibrium between the gravitational potential and its thermal and kinetic energy [19]. In equilibrium, one can use a spherically symmetric halo collapsing in an expanding universe to find that its mean density of 18π2 times the critical density ρc at the collapse time [20]. Recall that the density changes with a−3 = (1 + z)3 from cosmological effects. Given a halo mass Mh and the halo mean density ρh = 18π2 ρc (1 + z)3, three halo properties can be derived.
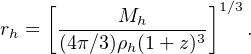 |
(3) |
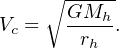 |
(4) |
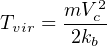 |
(5) |
CDM structure forms hierarchically with objects growing through a series of halo mergers. Galaxies exist at the centers of DM halos and are along for the ride throughout mergers, sparking galaxy interactions and mergers.
In this review, we are interested in the galaxies that form inside these halos, asking ourselves the question: How frequently do stars and galaxies form in the early universe, and generally when do they form? For a halo to host star formation, the gas must be able to cool and condense through some radiative process. Catastrophic cooling and collapse occurs when a halo reaches some critical temperature Tvir and associated mass Mh. From these critical points, we can estimate the abundance of the first stars and galaxies as a function of time. Their radiation will permeate the IGM, photoionizing and photoheating it. To study reionization from first principles point of view, we next overview the basic physics of photo-ionization.
2.3. Ionization and recombination
The radiation from the first luminous objects will ionize and heat the surrounding IGM once it escapes from their host halos. These are known as cosmological H ii regions. The ionization and recombination of hydrogen atoms (H + γ ↔ H+ + e−) are dominant processes in H ii regions and are illustrated in the Figure 3. Ionizations occur when photons with energies E > Ih = 13.6 eV interact with neutral hydrogen atoms, where their excess energies are subsequently thermalized. Recombinations occur when the Coulomb force attracts protons and electrons, which becomes efficient at temperatures T ≤ 104 K. One recombination releases a photon with an energy that is the sum of the kinetic energy of the electron and binding energy of the quantum state, Ih / n2. If the electron recombines into an excited state (n > 1), the electron will quickly decay into the ground state in a series of transitions.
In a region with ionizing radiation, the gas approaches ionization balance with the recombination rate equaling the ionization rate. We can equate these two rates and solve for the ionization fraction xe ≡ ne / nh of the gas at equilibrium. Here ne and nh are the electron and hydrogen number density, respectively.
To calculate the recombination rate, we can make the following assumptions: (i) the rate will be proportional to the product of the number density of protons np and electrons ne, (ii) the gas is pure hydrogen, giving np = ne, and (iii) the rate depends on the temperature and into which quantum state n it recombines. There are two rates associated with recombination:
The ionization rate can be calculated given some ionizing radiation flux. Photons will be absorbed as they travel through a medium with a neutral hydrogen number density, and the probability for a single absorption is quantified by the photoionization cross-section σHI ≈ 6.8 × 10−18 (E / 13.6 eV)−3 cm2 that decreases with photon energy. The cross-section is zero below 13.6 eV because the photon does not have sufficient energy to ionize hydrogen.
By equating the recombination and ionization rates, we can show that H ii regions are highly ionized, having ionization fractions nearly equal to one and neutral hydrogen fractions around 10−4. They are thus well described by a fully ionized plasma. The ionization flux, however, decreases as the distance squared from the star, resulting in the medium being the most ionized near radiation sources with it decreases rapidly with increasing distance.
2.4. Evolution of an H ii region
A radiation source can only provide a finite number of ionizing photons per second, so there must be some limit of ionizations possible in the surrounding region. Recombinations are happening concurrently with ionizations in the highly ionized H ii region. In some radial direction, if all of the ionizing photons are absorbed by newly recombined atoms inside the H ii region, there will be no more flux left at the ionization front. When this happens, the front stalls out and reaches an equilibrium [21]. We can determine the radius of the H ii region Rs, known as the Strömgren radius, by balancing the total number of ionizations and recombinations in a region. Assuming spherical symmetry and a static and uniform medium, we set these total numbers to be equal and solve for the radius. It is larger for more luminous sources (higher ionization rates) and for ambient gas with smaller densities (lower recombination rates).
Figure 4 depicts the evolution of an H ii region from when the star first ignites to the final stage when the ionization front stalls out. Initially the newborn star is surrounded by a dense medium from which it formed. The radiation front travels near the speed of light at early times through this dense gas, where the recombination rate is high. The H ii region is now heated to over 10,000 K and is encompassed by a cold ambient medium. The gas thus has a higher pressure than its surroundings and will start to expand. This marks the transition from the initial stage to the intermediate stage after the time it takes a sound wave to cross the H ii region. As the material is forced away from the star by the high pressure gas, it shocks with the ambient medium. The shock wave “sweeps up” most of the gas in its path and accumulates mass, leaving behind a more diffuse gas within the H ii region. As the density decreases, the recombination rate decreases accordingly. Thus, the Strömgren radius increases with time. Eventually the the H ii region comes into pressure equilibrium with the ambient medium, and both the shock front and ionization front stall out at the final Strömgren radius. This final equilibrium usually takes hundreds of millions of years to manifest, which is much longer than the lifetimes of massive stars, suggesting that this final stage is usually not realized in nature.
More relevant for reionization, this scenario of a central source ionizing its surrounding neutral gas can be extended to whole galaxies. Any ionizing radiation that escapes from the galaxy will create a cosmological H ii region that is the building block of reionization.
3 1 Mpc = 3.26 million light-years = 3.086 × 1024 cm. Back.
4 Friedmann-Lemaître-Robertson-Walker, all of who independently formulated this metric in the 1920’s and 1930’s. Back.