Copyright © 1990 by Annual Reviews. All rights reserved
| Annu. Rev. Astron. Astrophys. 1990. 28:
37-70 Copyright © 1990 by Annual Reviews. All rights reserved |
Each line of sight has its own ``extinction law'', or variation of
extinction with wavelength, usually expressed by A( ) / A(V) in this
article. This means of expressing the extinction law is not unique; it
has been common practice to use instead the ratios of two colors, E
(
) / A(V) in this
article. This means of expressing the extinction law is not unique; it
has been common practice to use instead the ratios of two colors, E
( - V) / E (B - V), where
E (
- V) / E (B - V), where
E ( - V) = A(
- V) = A( ) - A(V). The use of
A(V) as the
reference extinction is arbitrary, and it might be preferable to use
instead a longer wavelength, such as the J bandpass (
) - A(V). The use of
A(V) as the
reference extinction is arbitrary, and it might be preferable to use
instead a longer wavelength, such as the J bandpass ( 1.25 µm), because the
extinction law would then be virtually independent of line of sight (see
Section 2.1.3). The information content
of the extinction law is
independent of how the law is expressed, but certain relations (see
Section 2.1.1) become more obvious
when A(
1.25 µm), because the
extinction law would then be virtually independent of line of sight (see
Section 2.1.3). The information content
of the extinction law is
independent of how the law is expressed, but certain relations (see
Section 2.1.1) become more obvious
when A( ) / A(V) is used in place of
E (
) / A(V) is used in place of
E ( - V) / E (B - V).
- V) / E (B - V).
2.1.1.
Many authors have utilized the International Ultraviolet Explorer (IUE)
to make detailed studies of the UV extinction law of diffuse dust and
outer-cloud dust. There are considerable differences among the various
lines of sight. Cardelli, Clayton, and Mathis
[19,
20,
(hereinafter CCM89)] have used the UV observations of Fitzpatrick and Massa
[54
(hereinafter FM86),
55,
109],
with optical/NIR observations of the same stars, to explore the
relationships between various extinction laws over the entire
available interval of wavelengths. These observations were spread over
the sky and included both diffuse dust and lines of sight to the
Ophiuchus, Orion, and other molecular clouds, as well as H II
regions.
CCM89 used the
optical total-to-selective extinction ratio,
RV = A(V) / E (B - V), as a
parameter. (RV is determined by etrapolating NIR
extinction to infinite wavelength.)
Figure 1 shows the observed extinction
laws of many lines of sight, plotted against
RV-1, for several values of
The value of RV depends upon the environment along the
line of sight. A
direction through low-density ISM usually has a rather low value of
RV
(about 3.1). Lines of sight penetrating into a dense cloud, such as the
Ophiucus or Taurus molecular clouds, usually show 4
< RV < 6. However, it
is not possible to estimate RV quantitatively from the
environment of a
line of sight; for example, the star VI Cyg 12 lies behind a dense cloud
of dust, but has an RV of 3.1
(78), a value
appropriate for the diffuse ISM. As a further example,
RV
CCM89 fitted the
slopes of the various A(
The ``mean'' extinction laws of Savage and Mathis
(144)
and Seaton
(149)
are commonly used to correct observations for the presence
of dust. Both laws are reproduced closely if RV = 3.2
is substituted into the RV-dependent mean extinction
law given in CCM89. The panel in
Figure 2 shows the deviations of the
CCM89 mean
extinction law, with RV =
3.2 [from Seaton
(149)].
It is not surprising that mean extinction
laws correspond to an RV slightly higher than 3.1;
some lines of sight used in the averaging penetrate fairly dense regions.
Figure 1 shows that there is a continuous change
between properties of
diffuse dust, with RV
The differences of the extinctions between diffuse dust and outer-cloud
dust strongly affect any predictions of physical conditions inside of
clouds. Figure 2 shows tha outer-cloud
extinction laws, i.e. those with R
The fact that the extinction law depends so regularly on
RV suggests
that the processes which modify the sizes and/or the compositions of
grains must operate on all sizes simultaneously and quite
efficiently. One could imagine that the small and large grains would be
modified independently along various lines of sight , but such is not
the case. The consequences of the regularity of the various extinction
laws are considered in Section 7.
 ranging from the red to
almost the limit of the IUE spacecraft (1200 Å). There are fairly
tight linear relationships between A(
ranging from the red to
almost the limit of the IUE spacecraft (1200 Å). There are fairly
tight linear relationships between A( ) / A(V) and
RV-1 in each case, including the UV wavelengths.
) / A(V) and
RV-1 in each case, including the UV wavelengths.
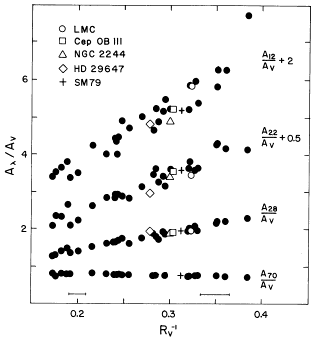
Figure 1. The observations of A(  ) / A(V) plotted against
RV-1, where RV =
A(V) / E(B - V) (from
CCM89). A12 refers to
1200 Å, A22 to 2175 Å,
A28 to 2800 Å,
and A70 to 7000 Å (the standard R
filter). The observational values of black dots are from Fitzpatrick
and Massa
(53). The regularity
of the observations and the scatter about the mean relationship are also
shown.
) / A(V) plotted against
RV-1, where RV =
A(V) / E(B - V) (from
CCM89). A12 refers to
1200 Å, A22 to 2175 Å,
A28 to 2800 Å,
and A70 to 7000 Å (the standard R
filter). The observational values of black dots are from Fitzpatrick
and Massa
(53). The regularity
of the observations and the scatter about the mean relationship are also
shown.
 3.0-3.5
in parts of the Taurus cloud
(159).
3.0-3.5
in parts of the Taurus cloud
(159).
 ) / A(V) -
RV-1 relations,
examples of which are shown in Figure 1, by an
analytic formula that represents the mean extinction law as a function of
RV. The expression
is not reproduced here. Figure 2 (from
CCM89)
shows the mean extinction
law for three values of RV as calculated from the
formula. Also shown
are actual observations with the same values of
RV. The central curve is
about as discrepant as actual observations are from the mean
relationship. The dispersion of individual extinction laws around that
mean law is shown in Figure 1 (from the spread
in the individual observed points) and in the panel in
Figure 2 (as error bars giving the
standard deviation). The lowest set of curves plotted
in Figure 2 are for
Herschel 36, an exciting star of the H II region M8 and considered to
have very ``peculiar'' extinction. Rather, Herschel 36 has a rather
peculiar value of RV (
) / A(V) -
RV-1 relations,
examples of which are shown in Figure 1, by an
analytic formula that represents the mean extinction law as a function of
RV. The expression
is not reproduced here. Figure 2 (from
CCM89)
shows the mean extinction
law for three values of RV as calculated from the
formula. Also shown
are actual observations with the same values of
RV. The central curve is
about as discrepant as actual observations are from the mean
relationship. The dispersion of individual extinction laws around that
mean law is shown in Figure 1 (from the spread
in the individual observed points) and in the panel in
Figure 2 (as error bars giving the
standard deviation). The lowest set of curves plotted
in Figure 2 are for
Herschel 36, an exciting star of the H II region M8 and considered to
have very ``peculiar'' extinction. Rather, Herschel 36 has a rather
peculiar value of RV ( 5.3), but a ``normal'' extinction law for that
value of RV. Note, however, that there are real
deviations from the mean
extinction law for any particular value of RV. These
deviations are especially large at 1200 Å, where the standard
deviation of A(
5.3), but a ``normal'' extinction law for that
value of RV. Note, however, that there are real
deviations from the mean
extinction law for any particular value of RV. These
deviations are especially large at 1200 Å, where the standard
deviation of A( ) / A(V)
from the mean extinction law is about 0.3. Extreme deviations might be
found in thefuture. Deviations will provide valuable information
regarding the processes which modify the grains.
) / A(V)
from the mean extinction law is about 0.3. Extreme deviations might be
found in thefuture. Deviations will provide valuable information
regarding the processes which modify the grains.
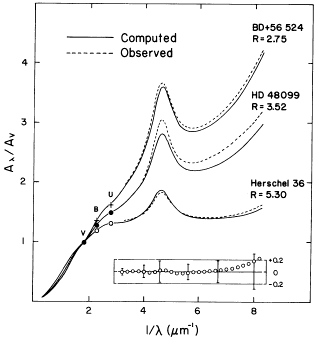
Figure 2. Three cases of a mean extinction law. Solid lines
are obtained by fitting the slopes of the A(  ) / A(V) -
RV-1
relationship (Figure 1) by an analytic formula
(CCM89), and dashed
lines are actual extinction laws of stars
(FM86)
with the appropriate values
of RV. The error bars in the lower panel show the
standard deviations of the observations of the entire sample
(54) from the
extinction law obtained from the formula. The open circles in the panel
show the deviations from the ``standard'' mean extinction law
(149) for
the value RV = 3.2, appropriate for the diffuse ISM.
) / A(V) -
RV-1
relationship (Figure 1) by an analytic formula
(CCM89), and dashed
lines are actual extinction laws of stars
(FM86)
with the appropriate values
of RV. The error bars in the lower panel show the
standard deviations of the observations of the entire sample
(54) from the
extinction law obtained from the formula. The open circles in the panel
show the deviations from the ``standard'' mean extinction law
(149) for
the value RV = 3.2, appropriate for the diffuse ISM.
 3.1, and outer-cloud dust, with large values
of RV. The twod esignations merely contrast one end of
the obseRVed
range of RV with the other.
3.1, and outer-cloud dust, with large values
of RV. The twod esignations merely contrast one end of
the obseRVed
range of RV with the other.
 4, rise much less
steeply at shorter wavelengths than diffuse dust. Consequently,
interstellar radiation incident upon a cloud can penetrate the cloud
much more easily than would be predicted from the Seaton or
Savage-Mathis extinction laws. Figure 3 shows
the mean radiation
intensity at the center of a cloud with a radial extinction of A(V) = 5
magnitudes (a typical value) computed using RV = 3.1,
and also with a typical outer-cloud dust value of RV =
5. The difference in the predicted mean intensities has large
implications for the physical processes in the cloud.
4, rise much less
steeply at shorter wavelengths than diffuse dust. Consequently,
interstellar radiation incident upon a cloud can penetrate the cloud
much more easily than would be predicted from the Seaton or
Savage-Mathis extinction laws. Figure 3 shows
the mean radiation
intensity at the center of a cloud with a radial extinction of A(V) = 5
magnitudes (a typical value) computed using RV = 3.1,
and also with a typical outer-cloud dust value of RV =
5. The difference in the predicted mean intensities has large
implications for the physical processes in the cloud.