Copyright © 1991 by Annual Reviews. All rights reserved
| Annu. Rev. Astron. Astrophys. 1991. 29:
325-362 Copyright © 1991 by Annual Reviews. All rights reserved |
4.2 Origin of Density Perturbations
Having decided the form of the density perturbations that is required,
we now turn to the actual mechanism by which these are produced. The
most natural choice, in the context of inflation, comes from the
quantum fluctuations in the scalar field  (t, x) driving the
inflation. The computation of classical perturbations generated by a
quantum field is a difficult and technically involved issue. Several
questions of principle are still unresolved in this calculation (see
e.g. 17,
94).
Since this review is primarily intended for the
astronomer, we limit discussion to the physical idea rather than to
the technical aspects of the calculation.
(t, x) driving the
inflation. The computation of classical perturbations generated by a
quantum field is a difficult and technically involved issue. Several
questions of principle are still unresolved in this calculation (see
e.g. 17,
94).
Since this review is primarily intended for the
astronomer, we limit discussion to the physical idea rather than to
the technical aspects of the calculation.
During inflation, the universe was assumed to be, on the average, in
a FRW state with small inhomogeneities. This implies that the source -
which is a classical scalar field  (t, x) - can be split as
(t, x) - can be split as  0 (t) +
f (t, x), where
0 (t) +
f (t, x), where  0 (t) denotes the average, homogeneous part
and f (t, x)
represents the spatially dependent fluctuating part. Since the energy
density due to a scalar field is
0 (t) denotes the average, homogeneous part
and f (t, x)
represents the spatially dependent fluctuating part. Since the energy
density due to a scalar field is  c2
c2  1/2
1/2  2, we obtain
2, we obtain
(where
where we have put
Since the average energy density during inflation is dominated by the
constant term V0, we have the density contrast
It might now appear that all we have to do is to compute the
quantities
In quantum theory, the field
The quantum state of the field can be specified by giving the quantum
state
The fluctuations in qk can be characterized by the dispersion
in this quantum state. (The mean value of the scalar field operator
<
In other words, the power spectrum of fluctuations
This is equivalent to defining the fluctuating classical field f
(t, x)
to be
This leads to the result
The procedure may be summarized as follows:
In quantum theory, the field Since the mean evolution of the scalar field
is described by a
homogeneous part We incorporate these quantum fluctuations in a
semiclassical manner
by taking the scalar field to be The density perturbations are calculated by
treating
The expression derived above gives the value of
where W (t) is the ratio between pressure p (t) and the
energy density
where we have used the fact
or using Eq. 42,
This is the final result.
The problem now reduces to computing
where we have taken the effective e-folding time N
This has been the most serious difficulty faced by all realistic
inflationary models: They produce too large an inhomogeneity. The
qualitative reason for this result can be found from Eq. 46. To obtain
slow roll-over and sufficient inflation, we need to keep 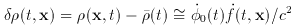
 (t) c2 = 1/2
(t) c2 = 1/2  0 (t)2 and we
have assumed
f <<
0 (t)2 and we
have assumed
f <<  0). The Fourier
transform will now give
0). The Fourier
transform will now give
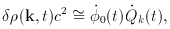
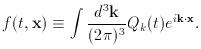
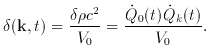
 0 (t)
and Qk (t) from the equation of motion for the scalar
field. For
0 (t)
and Qk (t) from the equation of motion for the scalar
field. For  0 (t)
we can use the mean evolution of the scalar field
during the slow roll-over phase and determine
0 (t)
we can use the mean evolution of the scalar field
during the slow roll-over phase and determine  0 (t) from the classical
solution. The fluctuating field f (t, x) is supposed to be some
classical object mimicking the quantum fluctuations. Such a quantity
is conceptually difficult to visualize and justify. What is usually
done is to choose some convenient quantum mechanical measure for
fluctuations and define Qk in terms of this quantity.
0 (t) from the classical
solution. The fluctuating field f (t, x) is supposed to be some
classical object mimicking the quantum fluctuations. Such a quantity
is conceptually difficult to visualize and justify. What is usually
done is to choose some convenient quantum mechanical measure for
fluctuations and define Qk in terms of this quantity.
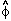 (t, x) and its Fourier coefficients
(t, x) and its Fourier coefficients
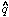 k(t)
will become operators related by
k(t)
will become operators related by
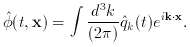
 k
(qk , t) of each of the modes
k
(qk , t) of each of the modes 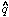 k. (One can think of
qk as
coordinates of a particle and
k. (One can think of
qk as
coordinates of a particle and  k (qk , t) as the
wavefunction describing this particle.)
k (qk , t) as the
wavefunction describing this particle.)
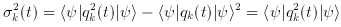
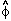 (t, x)> =
(t, x)> =  0 (t) is homogeneous; therefore, we have set
<
0 (t) is homogeneous; therefore, we have set
<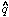 k> to zero
in the above expression. Note that we are interested only in the
k
k> to zero
in the above expression. Note that we are interested only in the
k  0
modes.) Expressing
0
modes.) Expressing 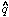 k in terms of
k in terms of 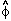 (t, x), it is easy to see that
(t, x), it is easy to see that
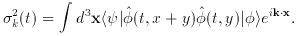
 k2 is
related to
the Fourier transform of the two-point-correlation function of the
scalar field. Since
k2 is
related to
the Fourier transform of the two-point-correlation function of the
scalar field. Since  k2 (t) appears to be a
good measure of quantum
fluctuations, we may attempt to define Qk (t) as
k2 (t) appears to be a
good measure of quantum
fluctuations, we may attempt to define Qk (t) as
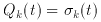
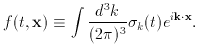
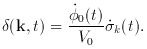
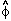 (t, x)
and its Fourier coefficient
(t, x)
and its Fourier coefficient
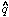 k(t)
become operators. In any quantum state, the variables will have
a mean value and fluctuations around this mean value.
k(t)
become operators. In any quantum state, the variables will have
a mean value and fluctuations around this mean value.
 0
(t), we expect the mean values of
0
(t), we expect the mean values of 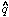 k to vanish (for
k
k to vanish (for
k  0); <
0); < |
|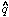 k(t)|
k(t)| > = 0. The fluctuations around these mean values,
however, characterized by
> = 0. The fluctuations around these mean values,
however, characterized by  k2 (t) = <
k2 (t) = < |
|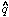 k2|
k2| >, do not vanish.
>, do not vanish.
 (t, x) =
(t, x) =  0 (t) f (t, x), where f (t,
x) is related to
0 (t) f (t, x), where f (t,
x) is related to  k (t) by
(41).
k (t) by
(41).
 (t, x) as a
classical object.
(t, x) as a
classical object.
 (k, t) in the
inflationary phase: ti < t <
tf. To compare this with observations we
need to know the value of
(k, t) in the
inflationary phase: ti < t <
tf. To compare this with observations we
need to know the value of  (k, t) at t = tenter (k),
that is, when the
perturbations enter the Hubble radius. Fortunately, an approximate
conservation law relates the value
(k, t) at t = tenter (k),
that is, when the
perturbations enter the Hubble radius. Fortunately, an approximate
conservation law relates the value  (k, tenter) with
(k, tenter) with  (k, texit), where
texit (k) is the time at which the relevant
perturbation ``leaves'' the
Hubble radius in the inflationary epoch
(8,
19,
46).
This law can be stated as
(k, texit), where
texit (k) is the time at which the relevant
perturbation ``leaves'' the
Hubble radius in the inflationary epoch
(8,
19,
46).
This law can be stated as
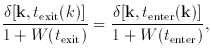
 (t)
c2 of the background (mean) medium: W (t) = p
(t) /
(t)
c2 of the background (mean) medium: W (t) = p
(t) /  (t)
c2. In the
inflationary phase with the scalar field,
(t)
c2. In the
inflationary phase with the scalar field,
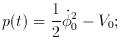
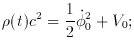
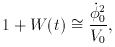
 02 << V0. In the
radiation-dominated phase
(at t = tenter), 1 + W = 4/3. Therefore
02 << V0. In the
radiation-dominated phase
(at t = tenter), 1 + W = 4/3. Therefore
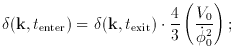
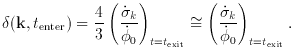
 k (t) and
k (t) and  0 (t), which can be
done once the potential V (
0 (t), which can be
done once the potential V ( )
is known. For a Coleman-Weinberg potential
(see Section 3.2),
detailed calculations give (see e.g. 17) the final result
)
is known. For a Coleman-Weinberg potential
(see Section 3.2),
detailed calculations give (see e.g. 17) the final result
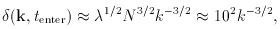
 50 and
50 and 
 0.1.
We see that the density perturbations have the correct spectrum but
too high an amplitude. To bring it down to the acceptable value of
about 10-4, we need to take the dimensionless parameter
0.1.
We see that the density perturbations have the correct spectrum but
too high an amplitude. To bring it down to the acceptable value of
about 10-4, we need to take the dimensionless parameter  to be about
10-13 ! This requires an extreme fine-tuning for a dimensionless
parameter, especially since we have no other motivation for such a
value.
to be about
10-13 ! This requires an extreme fine-tuning for a dimensionless
parameter, especially since we have no other motivation for such a
value.
 0 small, and
this tends to increase the value of
0 small, and
this tends to increase the value of  . We could have saved the
situation if it were possible to keep
. We could have saved the
situation if it were possible to keep  k arbitrarily small;
unfortunately, the inflationary phase induces a fluctuation of about
(H / 2
k arbitrarily small;
unfortunately, the inflationary phase induces a fluctuation of about
(H / 2 ) on any quantum field
due to field theoretical reasons (see
e.g. 18,
72).
This lower bound prevents us from getting sensible
values for
) on any quantum field
due to field theoretical reasons (see
e.g. 18,
72).
This lower bound prevents us from getting sensible
values for  unless we fine-tune
the dimensionless parameters of V (
unless we fine-tune
the dimensionless parameters of V ( )
(for a general discussion, see
92).
Several solutions have been
suggested in the literature to overcome this difficulty but none of
them appears compelling (see e.g.
42,
54,
62,
86,
90,
94,
108).
)
(for a general discussion, see
92).
Several solutions have been
suggested in the literature to overcome this difficulty but none of
them appears compelling (see e.g.
42,
54,
62,
86,
90,
94,
108).