


2. DATA
2.1. 4He
The primordial 4He abundance is best
determined from observations of HeII -> HeI recombination lines in
extragalactic HII (ionized hydrogen) regions.
There is a good collection of abundance information on the 4He mass
fraction, Y, O/H, and N/H in over 70 such regions
[8,
9,
10].
Since 4He is produced in stars along with heavier elements
such as Oxygen,
it is then expected that the primordial abundance of 4He can
be determined from the intercept of the correlation between Y and
O/H, namely YP = Y(O/H -> 0). A detailed
analysis
[11]
of the data found
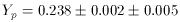 (1)
(1)
The first uncertainty is purely statistical and the second uncertainty is
an estimate of the systematic uncertainty in the primordial abundance
determination. The solid box for
4He in Figure 1 represents
the range (at 2 stat)
from (1). The dashed box extends this by including the systematic
uncertainty. The He data is shown in Figure 2.
stat)
from (1). The dashed box extends this by including the systematic
uncertainty. The He data is shown in Figure 2.
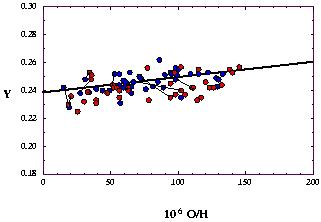
|
Figure 2. The Helium (Y) and Oxygen (O/H)
abundances in extragalactic HII regions, from refs.
[8]
and from ref.
[10].
Lines connect the same regions
observed by different groups. The regression shown leads to the primordial
4He abundance given in Eq. (1).
|
The helium abundance used to derive
(1) was determined using assumed electron densities n in the HII
regions obtained from SII data. Izotov, Thuan, & Lipovetsky
[9]
proposed a method based on several He
emission lines to ``self-consistently'' determine the electron density.
Their data using this method yields a higher primordial value
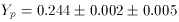 (2)
(2)
As one can see, the resulting primordial 4He abundance shows
significant sensitivity
to the method of abundance determination, leading one to
conclude that the
systematic uncertainty (which is already dominant) may be underestimated.
Indeed, the determination (1) of the primordial
abundance above is based on a combination of the data in refs.
[8],
which alone yield YP = 0.228 ± 0.005, and the
data of ref.
[10]
(based on SII densities) which give
0.239 ± 0.002. The abundance (2) is based solely on the self-consistent
method yields and the data of
[10].
One should also note that a recent determination
[12]
of the 4He abundance in a single object (the SMC) also using
the self
consistent method gives a primordial abundance of 0.234 ± 0.003
(actually, they observe Y = 0.240 ± 0.002 at [O/H] = -0.8,
where [O/H] refers to the log of the
Oxygen abundance relative to the solar value, in the units used in
Figure 2,
this corresponds to 106O/H = 135). Therefore, it will useful
to discuss some of the
key sources of the uncertainties in the He abundance determinations and
prospects for
improvement. To this end, I will briefly discuss, the importance of
reddening and
underlying absorption in the H line line measurements, Monte Carlo
methods for both H and He, and underlying absorption in He.
The He abundance is typically quoted relative to H, e.g., He line strengths are
measured relative to
 . The H data must
first be corrected for underlying absorption and reddening.
Beginning with an observed line flux
F(
. The H data must
first be corrected for underlying absorption and reddening.
Beginning with an observed line flux
F( , and an equivalent width
W(
, and an equivalent width
W( ), we can
parameterize the correction for underlying stellar absorption as
), we can
parameterize the correction for underlying stellar absorption as
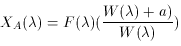 (3)
(3)
The parameter a is expected to be relatively insensitive to
wavelength. A reddening correction is applied to determine the
intrinsic line intensity
I( ) relative to
) relative to

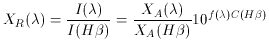 (4)
(4)
where f( ) represents
an assumed universal reddening law and
C(H
) represents
an assumed universal reddening law and
C(H ) is
the correction factor to be determined. By minimizing the differences between
XR(
) is
the correction factor to be determined. By minimizing the differences between
XR( ) to
theoretical values,
XT(
) to
theoretical values,
XT( ), for
), for
 =
H
=
H H
H and
H
and
H , one can determine the
parameters a and
C(H
, one can determine the
parameters a and
C(H )
self consistently
[13], and run a Monte
Carlo over the input data to test the robustness of the solution and to
determine the systematic uncertainty associated with these corrections.
)
self consistently
[13], and run a Monte
Carlo over the input data to test the robustness of the solution and to
determine the systematic uncertainty associated with these corrections.
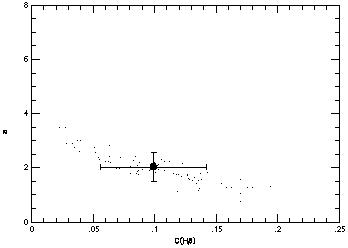
In Figure 3
[13],
the result of such a Monte-Carlo
based on synthetic data with an assumed correction of 2 Å for underlying
absorption and a value for
C(H )
= 0.1 is shown. The synthetic data were assumed to have an intrinsic
2% uncertainty. While the mean value of the Monte-Carlo results very
accurately reproduces the input parameters, the
spread in the values for a and
C(H
)
= 0.1 is shown. The synthetic data were assumed to have an intrinsic
2% uncertainty. While the mean value of the Monte-Carlo results very
accurately reproduces the input parameters, the
spread in the values for a and
C(H )
are considerably larger than one would have derived from the direct
)
are considerably larger than one would have derived from the direct
 2 minimization solution
due to the covariance in a and
C(H
2 minimization solution
due to the covariance in a and
C(H ).
).
|
Figure 3. A Monte Carlo determination of
the underlying absorption a (in Å ), and
reddening parameter
C(H ),
based on synthetic data. ),
based on synthetic data.
|
The uncertainties found for
 must next be
propagated into the analysis for 4He.
We can quantify the contribution to the overall He abundance
uncertainty due to the reddening correction by propagating the error in
eq. (3). Ignoring all other uncertainties in
XR(
must next be
propagated into the analysis for 4He.
We can quantify the contribution to the overall He abundance
uncertainty due to the reddening correction by propagating the error in
eq. (3). Ignoring all other uncertainties in
XR( ) =
I(
) =
I( ) /
I(H
) /
I(H ),
we would write
),
we would write
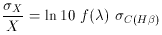 (5)
(5)
In the example discussed above,
 C(H
C(H ) are 0.237,
0.208, 0.109, -0.225, -0.345, -0.396, for He lines at
) are 0.237,
0.208, 0.109, -0.225, -0.345, -0.396, for He lines at

 3889, 4026, 4471, 5876,
6678, 7065, respectively. For the bluer lines, this correction alone is 1
- 2% and must be added in quadrature to any other observational errors
in XR. For the redder lines, this uncertainty is 3 -
4%. This
represents the minimum uncertainty which must be included in the
individual He I emission line strengths relative to
H
3889, 4026, 4471, 5876,
6678, 7065, respectively. For the bluer lines, this correction alone is 1
- 2% and must be added in quadrature to any other observational errors
in XR. For the redder lines, this uncertainty is 3 -
4%. This
represents the minimum uncertainty which must be included in the
individual He I emission line strengths relative to
H .
.
Next one can perform an analogous procedure to that described above
to determine the 4He abundance
[13]. We
again start with a set of observed quantities: line intensities
I( ) which include the
reddening correction previously determined along with
its associated uncertainty which includes the uncertainties in
C(H
) which include the
reddening correction previously determined along with
its associated uncertainty which includes the uncertainties in
C(H );
the equivalent width
W(
);
the equivalent width
W( ); and temperature
t. The Helium line intensities are scaled to
H
); and temperature
t. The Helium line intensities are scaled to
H and the singly ionized helium abundance is given by
and the singly ionized helium abundance is given by
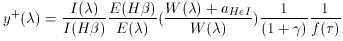 (6)
(6)
where E( ) /
E(H
) /
E(H ) is the
theoretical emissivity scaled to
H
) is the
theoretical emissivity scaled to
H .
The expression (6) also contains a correction factor for underlying
stellar absorption, parameterized now by aHeI, a
density dependent collisional correction factor,
(1 +
.
The expression (6) also contains a correction factor for underlying
stellar absorption, parameterized now by aHeI, a
density dependent collisional correction factor,
(1 +  )-1,
and a flourecence correction which depends on the optical depth
)-1,
and a flourecence correction which depends on the optical depth
 . Thus y+
implicitly depends on 3 unknowns, the
electron density, n, aHeI, and
. Thus y+
implicitly depends on 3 unknowns, the
electron density, n, aHeI, and
 .
.
One can use 3-6 lines to determine the
weighted average helium abundance,
 .
From
.
From  ,
we can calculate the
,
we can calculate the
 2 deviation from the average,
and minimize
2 deviation from the average,
and minimize  2, to determine
n, aHeI, and
2, to determine
n, aHeI, and  .
Uncertainties in the output parameters are also determined.
In principle, under the assumption of small values for the optical
depth
.
Uncertainties in the output parameters are also determined.
In principle, under the assumption of small values for the optical
depth  (3889), it is possible to use
only the three bright lines
(3889), it is possible to use
only the three bright lines
 4471,
4471,
 5876, and
5876, and
 6678 and still solve
self-consistently for He/H, density, and aHeI.
Of course, because these lines have relatively low sensitivities
to collisional enhancement, the derived uncertainties
in density will be large.
6678 and still solve
self-consistently for He/H, density, and aHeI.
Of course, because these lines have relatively low sensitivities
to collisional enhancement, the derived uncertainties
in density will be large.
The
addition of  7065 was proposed
[9]
as a density diagnostic and then,
7065 was proposed
[9]
as a density diagnostic and then,
 3889 was later added to
estimate the radiative
transfer effects (since these are important for
3889 was later added to
estimate the radiative
transfer effects (since these are important for
 7065).
Thus the five line method has the potential of self-consistently
determining the density and optical depth in the addition to
the 4He abundance.
The procedure described here differs somewhat from that proposed in
[9], in that
the
7065).
Thus the five line method has the potential of self-consistently
determining the density and optical depth in the addition to
the 4He abundance.
The procedure described here differs somewhat from that proposed in
[9], in that
the  2 above is based on
a straight weighted average, where as in
[9]
the difference of a ratio of He abundances (to one wavelength, say
2 above is based on
a straight weighted average, where as in
[9]
the difference of a ratio of He abundances (to one wavelength, say
 4471) to the theoretical
ratio is minimized. When the reference line is
particularly sensitive to a systematic effect such as underlying stellar
absorption, this uncertainty propagates to all lines this way.
4471) to the theoretical
ratio is minimized. When the reference line is
particularly sensitive to a systematic effect such as underlying stellar
absorption, this uncertainty propagates to all lines this way.
Adding  4026 as a diagnostic
line increases the leverage
on detecting underlying stellar absorption. This is because
the
4026 as a diagnostic
line increases the leverage
on detecting underlying stellar absorption. This is because
the  4026 line is a relatively
weak line. However, this also
requires that the input spectrum is a very high quality one.
4026 line is a relatively
weak line. However, this also
requires that the input spectrum is a very high quality one.
 4026 is also provides
exceptional leverage to underlying
stellar absorption because it is a singlet line and therefore
has very low sensitivity to collisional enhancement (i.e., n)
and optical depth (i.e.,
4026 is also provides
exceptional leverage to underlying
stellar absorption because it is a singlet line and therefore
has very low sensitivity to collisional enhancement (i.e., n)
and optical depth (i.e.,  (3889)) effects.
(3889)) effects.
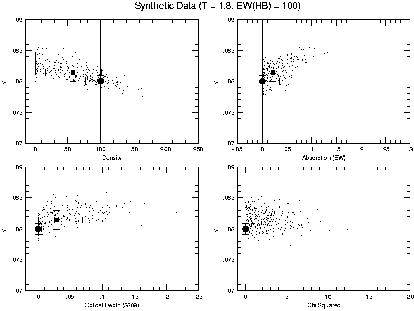
|
Figure 4. Results of modeling of 6
synthetic He I line observations. The
four panels show the results of a density = 100 cm-3,
aHeI = 0, and
 (3889) = 0 model. (3889) = 0 model.
|
As in the case of the hydrogen lines, Monte-Carlo
simulation of the He data can be used to test the robustness of the
solution for
n, aHeI, and  [13].
Figure 4 presents the
results of modeling of 6 synthetic He I line observations. The
four panels show the results of a density = 100 cm-3,
aHeI = 0, and
[13].
Figure 4 presents the
results of modeling of 6 synthetic He I line observations. The
four panels show the results of a density = 100 cm-3,
aHeI = 0, and
 (3889) = 0 model.
The solid lines show the input values (e.g., He/H = 0.080)
for the original calculated spectrum. The solid circles
(with error bars) show the results of the
(3889) = 0 model.
The solid lines show the input values (e.g., He/H = 0.080)
for the original calculated spectrum. The solid circles
(with error bars) show the results of the
 2 minimization solution
(with calculated errors) for the original synthetic input spectrum.
The small points show the results of Monte Carlo realizations
of the original input spectrum.
The solid squares (with error bars) show the means and dispersions
of the output values for the
2 minimization solution
(with calculated errors) for the original synthetic input spectrum.
The small points show the results of Monte Carlo realizations
of the original input spectrum.
The solid squares (with error bars) show the means and dispersions
of the output values for the
 2 minimization solutions of
the Monte Carlo realizations.
2 minimization solutions of
the Monte Carlo realizations.
Figure 4 demonstrates several important points. First,
the  2 minimization
solution finds the correct input
parameters with errors in He/H of about 1% (less than the
2% errors assumed on the input data, showing the power of
using multiple lines).
There is a systematic trend for the
Monte Carlo realizations to tend toward higher values of
He/H. This is because, the inclusion of errors has allowed
minimizations which find lower values of the density and
non-zero values of underlying absorption and optical depth.
Note that the size of
the error bars in He/H have expanded by roughly 50% as a result. We can
conclude from this that simply adding additional lines or physical
parameters in the minimization does not necessarily lead to the correct
results. In order to use the minimization routines effectively, one must
understand the role of the interdependencies of the individual
lines on the different physical parameters. Here we have shown
that trade-offs in underlying absorption and optical depth allow
for good solutions at densities which are too low and resulting
in helium abundance determinations which are too high.
Note that in the lower right panel of
Figure 4 that the values of the
2 minimization
solution finds the correct input
parameters with errors in He/H of about 1% (less than the
2% errors assumed on the input data, showing the power of
using multiple lines).
There is a systematic trend for the
Monte Carlo realizations to tend toward higher values of
He/H. This is because, the inclusion of errors has allowed
minimizations which find lower values of the density and
non-zero values of underlying absorption and optical depth.
Note that the size of
the error bars in He/H have expanded by roughly 50% as a result. We can
conclude from this that simply adding additional lines or physical
parameters in the minimization does not necessarily lead to the correct
results. In order to use the minimization routines effectively, one must
understand the role of the interdependencies of the individual
lines on the different physical parameters. Here we have shown
that trade-offs in underlying absorption and optical depth allow
for good solutions at densities which are too low and resulting
in helium abundance determinations which are too high.
Note that in the lower right panel of
Figure 4 that the values of the
 2 do not correlate
with the values of y+. The solutions at higher values of
absorption and y+ are equally valid as those at lower
absorption and y+.
2 do not correlate
with the values of y+. The solutions at higher values of
absorption and y+ are equally valid as those at lower
absorption and y+.
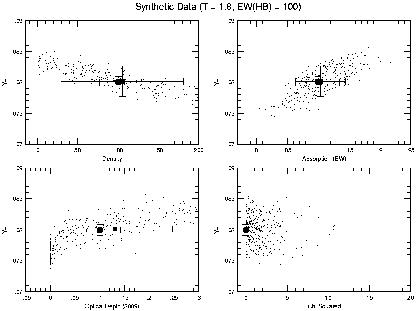
|
Figure 5. Similar plot to
Figure 4 except that the
underlying absorption is 0.1 Å and
 (3889) = 0.1. (3889) = 0.1.
|
Figure 5
shows the results of the Monte Carlo when both
 and aHeI
and aHeI
 0, and n = 100 cm-3.
It is encouraging that in perhaps more realistic cases where the input
parameters are non-zero, we are able to derive results very close to their
correct values. The average of Monte Carlo realizations is remarkably
close to the straight minimization for all of the derived parameters
(n, aHeI,
0, and n = 100 cm-3.
It is encouraging that in perhaps more realistic cases where the input
parameters are non-zero, we are able to derive results very close to their
correct values. The average of Monte Carlo realizations is remarkably
close to the straight minimization for all of the derived parameters
(n, aHeI,
 and
y+). However, there is an enormous dispersion in
these results due to the degeneracy in the solutions with respect to the
physical input parameters. This results in error estimates for
parameters which are significantly larger than in the straight
minimization. For example, the uncertainties in both the density and
optical depth are almost a factor of 3 times larger in the Monte Carlo.
When propagated into the uncertainty in the derived value for the He
abundance, we find that the uncertainty in the Monte Carlo result (which
we argue is a better, not merely more conservative, value) is a factor of
2.5 times the uncertainty obtained from a straight minimization using 6
line He lines. This amounts to an approximately 4% uncertainty in the He
abundance, despite the fact that we assumed (in the synthetic data) 2%
uncertainties in the input line strengths. This is an unavoidable
consequence of the method - the Monte Carlo routine explores the
degeneracies of the solutions and reveals the larger errors that
should be associated with the solutions.
and
y+). However, there is an enormous dispersion in
these results due to the degeneracy in the solutions with respect to the
physical input parameters. This results in error estimates for
parameters which are significantly larger than in the straight
minimization. For example, the uncertainties in both the density and
optical depth are almost a factor of 3 times larger in the Monte Carlo.
When propagated into the uncertainty in the derived value for the He
abundance, we find that the uncertainty in the Monte Carlo result (which
we argue is a better, not merely more conservative, value) is a factor of
2.5 times the uncertainty obtained from a straight minimization using 6
line He lines. This amounts to an approximately 4% uncertainty in the He
abundance, despite the fact that we assumed (in the synthetic data) 2%
uncertainties in the input line strengths. This is an unavoidable
consequence of the method - the Monte Carlo routine explores the
degeneracies of the solutions and reveals the larger errors that
should be associated with the solutions.
In Figure 6, I show the result of a single
case based on the data of ref.
[10]
for SBS1159+545.
Here, the helium abundance and density solutions are displayed.
The vertical and horizontal lines show the position of the solution in
[10].
The circle shows the position of the our solution to the minimization, and
the square shows the position of the mean of the Monte-Carlo distribution.
The spread shown here is significantly greater than the uncertainty quoted in
[10].
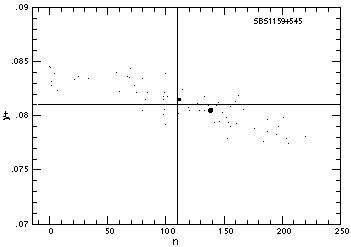
|
Figure 6. A Monte Carlo determination of
the helium abundance and electron density
(in cm-3) for the region SBS11159+545. Solutions for
a' and  are not shown here. are not shown here.
|






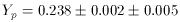
 stat)
from (1). The dashed box extends this by including the systematic
uncertainty. The He data is shown in Figure 2.
stat)
from (1). The dashed box extends this by including the systematic
uncertainty. The He data is shown in Figure 2.

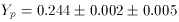
 . The H data must
first be corrected for underlying absorption and reddening.
Beginning with an observed line flux
F(
. The H data must
first be corrected for underlying absorption and reddening.
Beginning with an observed line flux
F( , and an equivalent width
W(
, and an equivalent width
W( ), we can
parameterize the correction for underlying stellar absorption as
), we can
parameterize the correction for underlying stellar absorption as
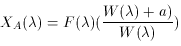
 ) relative to
) relative to

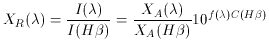
 ) represents
an assumed universal reddening law and
C(H
) represents
an assumed universal reddening law and
C(H ) is
the correction factor to be determined. By minimizing the differences between
XR(
) is
the correction factor to be determined. By minimizing the differences between
XR( ) to
theoretical values,
XT(
) to
theoretical values,
XT( ), for
), for
 =
H
=
H H
H and
H
and
H , one can determine the
parameters a and
C(H
, one can determine the
parameters a and
C(H )
self consistently
[13], and run a Monte
Carlo over the input data to test the robustness of the solution and to
determine the systematic uncertainty associated with these corrections.
)
self consistently
[13], and run a Monte
Carlo over the input data to test the robustness of the solution and to
determine the systematic uncertainty associated with these corrections.
 )
= 0.1 is shown. The synthetic data were assumed to have an intrinsic
2% uncertainty. While the mean value of the Monte-Carlo results very
accurately reproduces the input parameters, the
spread in the values for a and
C(H
)
= 0.1 is shown. The synthetic data were assumed to have an intrinsic
2% uncertainty. While the mean value of the Monte-Carlo results very
accurately reproduces the input parameters, the
spread in the values for a and
C(H )
are considerably larger than one would have derived from the direct
)
are considerably larger than one would have derived from the direct
 2 minimization solution
due to the covariance in a and
C(H
2 minimization solution
due to the covariance in a and
C(H ).
).

 ),
based on synthetic data.
),
based on synthetic data.
 must next be
propagated into the analysis for 4He.
We can quantify the contribution to the overall He abundance
uncertainty due to the reddening correction by propagating the error in
eq. (3). Ignoring all other uncertainties in
XR(
must next be
propagated into the analysis for 4He.
We can quantify the contribution to the overall He abundance
uncertainty due to the reddening correction by propagating the error in
eq. (3). Ignoring all other uncertainties in
XR( ) =
I(
) =
I( ) /
I(H
) /
I(H ),
we would write
),
we would write
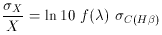
 C(H
C(H ) are 0.237,
0.208, 0.109, -0.225, -0.345, -0.396, for He lines at
) are 0.237,
0.208, 0.109, -0.225, -0.345, -0.396, for He lines at

 3889, 4026, 4471, 5876,
6678, 7065, respectively. For the bluer lines, this correction alone is 1
- 2% and must be added in quadrature to any other observational errors
in XR. For the redder lines, this uncertainty is 3 -
4%. This
represents the minimum uncertainty which must be included in the
individual He I emission line strengths relative to
H
3889, 4026, 4471, 5876,
6678, 7065, respectively. For the bluer lines, this correction alone is 1
- 2% and must be added in quadrature to any other observational errors
in XR. For the redder lines, this uncertainty is 3 -
4%. This
represents the minimum uncertainty which must be included in the
individual He I emission line strengths relative to
H .
.
 ) which include the
reddening correction previously determined along with
its associated uncertainty which includes the uncertainties in
C(H
) which include the
reddening correction previously determined along with
its associated uncertainty which includes the uncertainties in
C(H );
the equivalent width
W(
);
the equivalent width
W( ); and temperature
t. The Helium line intensities are scaled to
H
); and temperature
t. The Helium line intensities are scaled to
H and the singly ionized helium abundance is given by
and the singly ionized helium abundance is given by
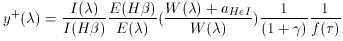
 ) /
E(H
) /
E(H ) is the
theoretical emissivity scaled to
H
) is the
theoretical emissivity scaled to
H .
The expression (6) also contains a correction factor for underlying
stellar absorption, parameterized now by aHeI, a
density dependent collisional correction factor,
(1 +
.
The expression (6) also contains a correction factor for underlying
stellar absorption, parameterized now by aHeI, a
density dependent collisional correction factor,
(1 +  )-1,
and a flourecence correction which depends on the optical depth
)-1,
and a flourecence correction which depends on the optical depth
 . Thus y+
implicitly depends on 3 unknowns, the
electron density, n, aHeI, and
. Thus y+
implicitly depends on 3 unknowns, the
electron density, n, aHeI, and
 .
.
 .
From
.
From  ,
we can calculate the
,
we can calculate the
 2 deviation from the average,
and minimize
2 deviation from the average,
and minimize  2, to determine
n, aHeI, and
2, to determine
n, aHeI, and  .
Uncertainties in the output parameters are also determined.
In principle, under the assumption of small values for the optical
depth
.
Uncertainties in the output parameters are also determined.
In principle, under the assumption of small values for the optical
depth  (3889), it is possible to use
only the three bright lines
(3889), it is possible to use
only the three bright lines
 4471,
4471,
 5876, and
5876, and
 6678 and still solve
self-consistently for He/H, density, and aHeI.
Of course, because these lines have relatively low sensitivities
to collisional enhancement, the derived uncertainties
in density will be large.
6678 and still solve
self-consistently for He/H, density, and aHeI.
Of course, because these lines have relatively low sensitivities
to collisional enhancement, the derived uncertainties
in density will be large.
 7065 was proposed
[9]
as a density diagnostic and then,
7065 was proposed
[9]
as a density diagnostic and then,
 3889 was later added to
estimate the radiative
transfer effects (since these are important for
3889 was later added to
estimate the radiative
transfer effects (since these are important for
 7065).
Thus the five line method has the potential of self-consistently
determining the density and optical depth in the addition to
the 4He abundance.
The procedure described here differs somewhat from that proposed in
[9], in that
the
7065).
Thus the five line method has the potential of self-consistently
determining the density and optical depth in the addition to
the 4He abundance.
The procedure described here differs somewhat from that proposed in
[9], in that
the  2 above is based on
a straight weighted average, where as in
[9]
the difference of a ratio of He abundances (to one wavelength, say
2 above is based on
a straight weighted average, where as in
[9]
the difference of a ratio of He abundances (to one wavelength, say
 4471) to the theoretical
ratio is minimized. When the reference line is
particularly sensitive to a systematic effect such as underlying stellar
absorption, this uncertainty propagates to all lines this way.
4471) to the theoretical
ratio is minimized. When the reference line is
particularly sensitive to a systematic effect such as underlying stellar
absorption, this uncertainty propagates to all lines this way.
 4026 as a diagnostic
line increases the leverage
on detecting underlying stellar absorption. This is because
the
4026 as a diagnostic
line increases the leverage
on detecting underlying stellar absorption. This is because
the  4026 line is a relatively
weak line. However, this also
requires that the input spectrum is a very high quality one.
4026 line is a relatively
weak line. However, this also
requires that the input spectrum is a very high quality one.
 4026 is also provides
exceptional leverage to underlying
stellar absorption because it is a singlet line and therefore
has very low sensitivity to collisional enhancement (i.e., n)
and optical depth (i.e.,
4026 is also provides
exceptional leverage to underlying
stellar absorption because it is a singlet line and therefore
has very low sensitivity to collisional enhancement (i.e., n)
and optical depth (i.e.,  (3889)) effects.
(3889)) effects.

 (3889) = 0 model.
(3889) = 0 model.
 [13].
Figure 4 presents the
results of modeling of 6 synthetic He I line observations. The
four panels show the results of a density = 100 cm-3,
aHeI = 0, and
[13].
Figure 4 presents the
results of modeling of 6 synthetic He I line observations. The
four panels show the results of a density = 100 cm-3,
aHeI = 0, and
 (3889) = 0 model.
The solid lines show the input values (e.g., He/H = 0.080)
for the original calculated spectrum. The solid circles
(with error bars) show the results of the
(3889) = 0 model.
The solid lines show the input values (e.g., He/H = 0.080)
for the original calculated spectrum. The solid circles
(with error bars) show the results of the
 2 minimization solution
(with calculated errors) for the original synthetic input spectrum.
The small points show the results of Monte Carlo realizations
of the original input spectrum.
The solid squares (with error bars) show the means and dispersions
of the output values for the
2 minimization solution
(with calculated errors) for the original synthetic input spectrum.
The small points show the results of Monte Carlo realizations
of the original input spectrum.
The solid squares (with error bars) show the means and dispersions
of the output values for the
 2 minimization solutions of
the Monte Carlo realizations.
2 minimization solutions of
the Monte Carlo realizations.
 2 minimization
solution finds the correct input
parameters with errors in He/H of about 1% (less than the
2% errors assumed on the input data, showing the power of
using multiple lines).
There is a systematic trend for the
Monte Carlo realizations to tend toward higher values of
He/H. This is because, the inclusion of errors has allowed
minimizations which find lower values of the density and
non-zero values of underlying absorption and optical depth.
Note that the size of
the error bars in He/H have expanded by roughly 50% as a result. We can
conclude from this that simply adding additional lines or physical
parameters in the minimization does not necessarily lead to the correct
results. In order to use the minimization routines effectively, one must
understand the role of the interdependencies of the individual
lines on the different physical parameters. Here we have shown
that trade-offs in underlying absorption and optical depth allow
for good solutions at densities which are too low and resulting
in helium abundance determinations which are too high.
Note that in the lower right panel of
Figure 4 that the values of the
2 minimization
solution finds the correct input
parameters with errors in He/H of about 1% (less than the
2% errors assumed on the input data, showing the power of
using multiple lines).
There is a systematic trend for the
Monte Carlo realizations to tend toward higher values of
He/H. This is because, the inclusion of errors has allowed
minimizations which find lower values of the density and
non-zero values of underlying absorption and optical depth.
Note that the size of
the error bars in He/H have expanded by roughly 50% as a result. We can
conclude from this that simply adding additional lines or physical
parameters in the minimization does not necessarily lead to the correct
results. In order to use the minimization routines effectively, one must
understand the role of the interdependencies of the individual
lines on the different physical parameters. Here we have shown
that trade-offs in underlying absorption and optical depth allow
for good solutions at densities which are too low and resulting
in helium abundance determinations which are too high.
Note that in the lower right panel of
Figure 4 that the values of the
 2 do not correlate
with the values of y+. The solutions at higher values of
absorption and y+ are equally valid as those at lower
absorption and y+.
2 do not correlate
with the values of y+. The solutions at higher values of
absorption and y+ are equally valid as those at lower
absorption and y+.

 (3889) = 0.1.
(3889) = 0.1.
 and aHeI
and aHeI
 0, and n = 100 cm-3.
It is encouraging that in perhaps more realistic cases where the input
parameters are non-zero, we are able to derive results very close to their
correct values. The average of Monte Carlo realizations is remarkably
close to the straight minimization for all of the derived parameters
(n, aHeI,
0, and n = 100 cm-3.
It is encouraging that in perhaps more realistic cases where the input
parameters are non-zero, we are able to derive results very close to their
correct values. The average of Monte Carlo realizations is remarkably
close to the straight minimization for all of the derived parameters
(n, aHeI,
 and
y+). However, there is an enormous dispersion in
these results due to the degeneracy in the solutions with respect to the
physical input parameters. This results in error estimates for
parameters which are significantly larger than in the straight
minimization. For example, the uncertainties in both the density and
optical depth are almost a factor of 3 times larger in the Monte Carlo.
When propagated into the uncertainty in the derived value for the He
abundance, we find that the uncertainty in the Monte Carlo result (which
we argue is a better, not merely more conservative, value) is a factor of
2.5 times the uncertainty obtained from a straight minimization using 6
line He lines. This amounts to an approximately 4% uncertainty in the He
abundance, despite the fact that we assumed (in the synthetic data) 2%
uncertainties in the input line strengths. This is an unavoidable
consequence of the method - the Monte Carlo routine explores the
degeneracies of the solutions and reveals the larger errors that
should be associated with the solutions.
and
y+). However, there is an enormous dispersion in
these results due to the degeneracy in the solutions with respect to the
physical input parameters. This results in error estimates for
parameters which are significantly larger than in the straight
minimization. For example, the uncertainties in both the density and
optical depth are almost a factor of 3 times larger in the Monte Carlo.
When propagated into the uncertainty in the derived value for the He
abundance, we find that the uncertainty in the Monte Carlo result (which
we argue is a better, not merely more conservative, value) is a factor of
2.5 times the uncertainty obtained from a straight minimization using 6
line He lines. This amounts to an approximately 4% uncertainty in the He
abundance, despite the fact that we assumed (in the synthetic data) 2%
uncertainties in the input line strengths. This is an unavoidable
consequence of the method - the Monte Carlo routine explores the
degeneracies of the solutions and reveals the larger errors that
should be associated with the solutions.

 are not shown here.
are not shown here.