


It is fortunate that large column densities of material (equation 3)
are expected close to the active nucleus, for there is an enormous
radiation pressure on dusty gas directly exposed to a quasar's UV
flux. The opacity of a single grain is  / m
/ m  2 x
104 (0.1 µ/a) cm2
g-1. If the grains are coupled by collisions or Lorentz
forces to gas,
then with a Galactic gas to dust ratio, the total opacity is
2 x
104 (0.1 µ/a) cm2
g-1. If the grains are coupled by collisions or Lorentz
forces to gas,
then with a Galactic gas to dust ratio, the total opacity is
 gr
gr
 200
cm2 g-1 (roughly the cross section to mass ratio
of an interstellar
cloud with Av ~ 1). This is nearly 103
times larger than the Thomson
opacity
200
cm2 g-1 (roughly the cross section to mass ratio
of an interstellar
cloud with Av ~ 1). This is nearly 103
times larger than the Thomson
opacity  T = 0.4
cm2 g-1 which defines the Eddington limit, so
radiation pressure will tend to expel unshielded dusty gas from all
but the outer edges of the host galaxy. In the absence of forces other
than radiation pressure and gravity, at radius rpc gas
in which dust survives will reach a terminal velocity
T = 0.4
cm2 g-1 which defines the Eddington limit, so
radiation pressure will tend to expel unshielded dusty gas from all
but the outer edges of the host galaxy. In the absence of forces other
than radiation pressure and gravity, at radius rpc gas
in which dust survives will reach a terminal velocity
where
The component of this radiation force normal to the disk surface,
which must be balanced by vertical pressure gradients in a
quasi-static situation, would destroy in a dynamical time any warp in
a disk with
The column density of a Stromgren length is
Free-free emission from the photoionized surface layers of the
warped disk with electron density ne will be optically
thin at
frequencies
where g(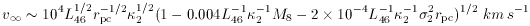
 gr =
102
gr =
102  2
cm2 g-1. The innermost radius at which dust can
survive (section 6) defines a characteristic
velocity v,sub>max ~ 2104
L461/4
2
cm2 g-1. The innermost radius at which dust can
survive (section 6) defines a characteristic
velocity v,sub>max ~ 2104
L461/4  21/2 km s-1.
21/2 km s-1.
 <
50rpc-1 cos
<
50rpc-1 cos  . Since this is generally less than
. Since this is generally less than
 sg
(equation 3), warps can survive. The tangential force along the disk
surface cannot be balanced, so the surface layers will be ablated. The
radiation force acts primarily only on a thin layer of column density
~
sg
(equation 3), warps can survive. The tangential force along the disk
surface cannot be balanced, so the surface layers will be ablated. The
radiation force acts primarily only on a thin layer of column density
~  gr-1. Large-scale
Kelvin-Helmholtz instabilities might couple the
motion of that layer to underlying material, but the resulting shocks
would destroy the dust in the surface layers and thus reduce the rate
of ablation. With and without coupling, we find that the ablation
timescale is considerably longer than the inferred inflow timescales
(see section 4), so the disk is likely to
survive. The fate of the
dust in the surface layers is less clear. The dust can be destroyed by
sputtering if it develops a high speed
gr-1. Large-scale
Kelvin-Helmholtz instabilities might couple the
motion of that layer to underlying material, but the resulting shocks
would destroy the dust in the surface layers and thus reduce the rate
of ablation. With and without coupling, we find that the ablation
timescale is considerably longer than the inferred inflow timescales
(see section 4), so the disk is likely to
survive. The fate of the
dust in the surface layers is less clear. The dust can be destroyed by
sputtering if it develops a high speed  v relative to the surrounding
gas. Collisional coupling maintains (
v relative to the surrounding
gas. Collisional coupling maintains ( v)2 ~ prad /
v)2 ~ prad /
 gas
(proportional to
the ionization parameter) small enough near the disk that grains can
survive. But since accelerated dust must pass through shocks to follow
a warped surface, it may well be destroyed long before it and its
associated gas reach the terminal speed (5).
gas
(proportional to
the ionization parameter) small enough near the disk that grains can
survive. But since accelerated dust must pass through shocks to follow
a warped surface, it may well be destroyed long before it and its
associated gas reach the terminal speed (5).
 s = 0.05
s = 0.05
 T4 g cm-1,
where
T4 g cm-1,
where  is the ratio of ionizing
radiation pressure to gas pressure,
and 104 T4 K is the temperature of the
photoionized gas. Plausible
transition-zone disks have
is the ratio of ionizing
radiation pressure to gas pressure,
and 104 T4 K is the temperature of the
photoionized gas. Plausible
transition-zone disks have 
 100±2 at all
radii. Except in the
outskirts of the galaxy
100±2 at all
radii. Except in the
outskirts of the galaxy  sg >>
sg >>  c, so
only a thin surface layer will
be photoionized. If dust survives in this layer (as is especially
likely in the low-density outer regions of the galaxy) resonance line
emission from this layer will be converted into infrared photons,
while other emission lines will be heavily reddened. If dust is
destroyed (as is likely in the inner regions), the surface may
contribute to (and perhaps dominate!) the emission line flux from the AGN
(Collin-Souffrin
1987).
c, so
only a thin surface layer will
be photoionized. If dust survives in this layer (as is especially
likely in the low-density outer regions of the galaxy) resonance line
emission from this layer will be converted into infrared photons,
while other emission lines will be heavily reddened. If dust is
destroyed (as is likely in the inner regions), the surface may
contribute to (and perhaps dominate!) the emission line flux from the AGN
(Collin-Souffrin
1987).
 > 1010
(ne / 105 cm-3)1/2
Hz, so radio frequency free-free
emission will come predominantly from the outer parts of the disk,
while free-free at millimeter wavelengths could have a comparable
contribution from the inner parsecs. It is easy to show that the
free-free luminosity density L
> 1010
(ne / 105 cm-3)1/2
Hz, so radio frequency free-free
emission will come predominantly from the outer parts of the disk,
while free-free at millimeter wavelengths could have a comparable
contribution from the inner parsecs. It is easy to show that the
free-free luminosity density L (ff) (the optically thin free-free
emissivity, integrated over the photoionized volume), is simply
related to the infrared luminosity re-radiated by the underlying
(and/or cospatial, if dust survives in the photoionized surface) gas:
(ff) (the optically thin free-free
emissivity, integrated over the photoionized volume), is simply
related to the infrared luminosity re-radiated by the underlying
(and/or cospatial, if dust survives in the photoionized surface) gas:
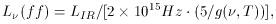
 , T) is the
Gaunt factor. The resulting free-free
luminosities are comparable to those of the flat-spectrum components
observed in quasars by
Antonucci and
Barvainis (1988),
and also to the
level of the radio detections in most PG quasars (Kellermanm reported
in Sanders et
al. 1989).
, T) is the
Gaunt factor. The resulting free-free
luminosities are comparable to those of the flat-spectrum components
observed in quasars by
Antonucci and
Barvainis (1988),
and also to the
level of the radio detections in most PG quasars (Kellermanm reported
in Sanders et
al. 1989).