


The rate of sublimation of a dust grain at temperature T is given (in g cm-2 s-1) by
where the index i runs over all equilibrium gas-phase species (e.g. C,
C2, CO, etc. for graphite grains), pi is
the partial pressure of
species i, Si(T) ~ 1 is the sticking fraction
for molecules colliding
with the grain surface, and psi is the saturation
vapor pressure for
species i. The saturation vapor pressure is given by
where
The gas pressure in an
This pressure is comparable to the pressure ~ 10-2 dyn
cm-2 in
broad-line clouds. Since the solar abundance of carbon, C/H = 4 x
10-4,
the partial pressure of carbon, were it all in the gas phase, would be
At radii ~ 1 pc, grains grow at an impressive rate: a /
When the dust sublimates, the gas loses its primary opacity and
coolant. As the temperature rises above ~ 3000 K, most common
molecules are destroyed, and the opacity drops precipitously by
several orders of magnitude
(Alexander et
al. 1983).
The gas in the
interior of the disk is then unable to remain in thermal equilibrium
at temperatures 2000 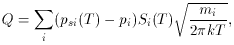
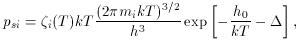
 i is the product of the rotational,
vibrational, and electronic
partition functions for the gas-phase species i, and
h0 is the heat of
sublimation at zero temperature, on a per atom basis.
i is the product of the rotational,
vibrational, and electronic
partition functions for the gas-phase species i, and
h0 is the heat of
sublimation at zero temperature, on a per atom basis.
 (T) is a
complicated expression involving integrals of the specific heat of the solid
(Reif 1965,
p. 367). Graphite (h0 / k =
8.58 x 104 K to C, h0 / k =
9.82 x 104 K to C2, h0 /
k = 9.45 x 104 K to C3,
Kelley 1973)
is the most refractory substance (with the exception of Tungsten!); silicate
grains have h0 / k
(T) is a
complicated expression involving integrals of the specific heat of the solid
(Reif 1965,
p. 367). Graphite (h0 / k =
8.58 x 104 K to C, h0 / k =
9.82 x 104 K to C2, h0 /
k = 9.45 x 104 K to C3,
Kelley 1973)
is the most refractory substance (with the exception of Tungsten!); silicate
grains have h0 / k
 6.6 x 104 K. We
have fitted the thermodynamic data
and sublimation measurements of graphite in vacuum
(Kelley 1973),
and find that the saturation vapor pressure of the dominant gas-phase
constituent is well fitted by
6.6 x 104 K. We
have fitted the thermodynamic data
and sublimation measurements of graphite in vacuum
(Kelley 1973),
and find that the saturation vapor pressure of the dominant gas-phase
constituent is well fitted by
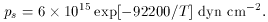
 accretion disk is
accretion disk is
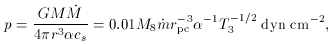
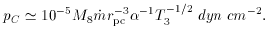
 ~ 5n9
(a / 0.1
µm) yr; in fact the temperatures and densities are quite similar to
those in red-giant winds where interstellar dust is believed to
form. [But here the grain and gas temperatures need not be equal: the
ratio of a grain's radiative cooling luminosity to the rate at which
it exchanges energy with gas via collisions is L/H =
10n11-1 Tg,35
/ TH,33/2,
where the grain temperature is 103 Tg,3 K
and the gas temperature and
density are 103 TH,3 and 1011
n11 cm-3, respectively]. However, comparing
with equation (7) and equation (9), we see that when the grain
temperatures Tg exceed 2000 K, graphite grains will
certainly begin to
sublimate rather than grow. For Tg > 2100 K, the
timescale for sublimation of a 1 µm graphite grain becomes
shorter than 103 yr, the
timescale on which in could be replenished by inflow. From
figure 1,
we see that this temperature is reached at ~ 0.3 pc in our fiducial quasar.
~ 5n9
(a / 0.1
µm) yr; in fact the temperatures and densities are quite similar to
those in red-giant winds where interstellar dust is believed to
form. [But here the grain and gas temperatures need not be equal: the
ratio of a grain's radiative cooling luminosity to the rate at which
it exchanges energy with gas via collisions is L/H =
10n11-1 Tg,35
/ TH,33/2,
where the grain temperature is 103 Tg,3 K
and the gas temperature and
density are 103 TH,3 and 1011
n11 cm-3, respectively]. However, comparing
with equation (7) and equation (9), we see that when the grain
temperatures Tg exceed 2000 K, graphite grains will
certainly begin to
sublimate rather than grow. For Tg > 2100 K, the
timescale for sublimation of a 1 µm graphite grain becomes
shorter than 103 yr, the
timescale on which in could be replenished by inflow. From
figure 1,
we see that this temperature is reached at ~ 0.3 pc in our fiducial quasar.
 T
T  7000 K, and
must inevitably heat. Above ~ 104 K, the opacity rises
abruptly to near its former level as hydrogen
is ionized, providing the gas with a new thermal equilibrium
state. Unless there is no warp (or down-scattering of radiation onto
the disk from electrons or a jet), the transition disk at r < 0.3 pc
is thus constrained by the heating from the central source to be
optically thin, with T ~ 104 K, until r
7000 K, and
must inevitably heat. Above ~ 104 K, the opacity rises
abruptly to near its former level as hydrogen
is ionized, providing the gas with a new thermal equilibrium
state. Unless there is no warp (or down-scattering of radiation onto
the disk from electrons or a jet), the transition disk at r < 0.3 pc
is thus constrained by the heating from the central source to be
optically thin, with T ~ 104 K, until r
 0.02 pc, when the incident
flux can be carried by optically thick thermal emission, and the
temperature will begin to rise above 104 K in the accretion
disk. The
absence of thermalized emission from material with temperatures 2000
0.02 pc, when the incident
flux can be carried by optically thick thermal emission, and the
temperature will begin to rise above 104 K in the accretion
disk. The
absence of thermalized emission from material with temperatures 2000
 T
T  7000 K provides
a natural explanation for the minimum in
7000 K provides
a natural explanation for the minimum in
 L
L at
at  = 1014.5 Hz (
= 1014.5 Hz ( = 1
µm) observed in almost all quasars
(Neugebauer et
al. 1989).
[The reader may mentally add an accretion disk spectrum to
the right of figure 2]. Since in
this interpretation the frequency is
a universal constant, determined (up to very slowly varying
logarithms) by the heats of sublimation and dissociation of dust and
molecules, and by the ionization of hydrogen, the minimum in the
reradiated
= 1
µm) observed in almost all quasars
(Neugebauer et
al. 1989).
[The reader may mentally add an accretion disk spectrum to
the right of figure 2]. Since in
this interpretation the frequency is
a universal constant, determined (up to very slowly varying
logarithms) by the heats of sublimation and dissociation of dust and
molecules, and by the ionization of hydrogen, the minimum in the
reradiated  L
L will always be present, and
observable unless filled in
by starlight or a non-thermal contribution to the spectrum.
will always be present, and
observable unless filled in
by starlight or a non-thermal contribution to the spectrum.