Formation of Structure in the Universe

1.2 Cosmology Basics

It is assumed here that Einstein's general theory of relativity (GR) accurately describes gravity. Although it is important to appreciate that there is no observational confirmation of this on scales larger than about 1 Mpc, the tests of GR on smaller scales are becoming increasingly precise, especially with pulsars in binary star systems (Will 1981, 1986, 1990; Taylor 1994). On galaxy and cluster scales, the general agreement between the mass estimated by velocity measurements and by gravitational lensing provides evidence supporting standard gravity. There are two other reasons most cosmologists believe in GR: it is conceptually so beautifully simple that it is hard to believe it could be wrong, and anyway it has no serious theoretical competition. Nevertheless, since a straightforward interpretation of the available data in the context of the standard theory of gravity leads to the disquieting conclusion that most of the matter in the universe is dark, there have been suggestions that perhaps our theory of gravity is inadequate on large scales. The suggested alternatives are mentioned briefly in Section 1.2.2.

The ``Copernican'' or ``cosmological'' principle is logically independent of our theory of gravity, so it is appropriate to state it before discussing GR further. First, some definitions are necessary:

A co-moving observer is at rest and unaccelerated with respect to nearby material (in practice, with respect to the center of mass of galaxies within, say, 100h^-1 Mpc).
The universe is homogeneous if all co-moving observers see identical properties.
The universe is isotropic if all co-moving observers see no preferred direction.

The cosmological principle asserts that the universe is homogeneous and isotropic on large scales. (Isotropy about at least three points actually implies homogeneity, but the counterexample of a cylinder shows that the reverse is not true.) In reality, the matter distribution in the universe is exceedingly inhomogeneous on small scales, and increasingly homogeneous on scales approaching the entire horizon. The cosmological principle is in practice the assumption that for cosmological purposes we can neglect this inhomogeneity, or treat it perturbatively. This has now been put on an improved basis, based on the observed isotropy of the cosmic background radiation and the (partially testable) Copernican assumption that other observers also see a nearly homogeneous CBR. The ``COBE-Copernicus'' theorem (Stoeger, Maartens, & Ellis 1995; Maartens, Ellis, & Stoeger 1995; reviewed by Ellis 1996) asserts that if all comoving observers measure the cosmic microwave background radiation to be almost isotropic in a region of the expanding universe, then the universe is locally almost spatially homogeneous and isotropic in that region.

The great advantage of assuming homogeneity is that our own cosmic neighborhood becomes representative of the whole universe, and the range of cosmological models to be considered is also enormously reduced. The cosmological principle also implies the existence of a universal cosmic time, since all observers see the same sequence of cosmic events with which to synchronize their clocks. (This assumption is sometimes explicitly included in the statement of the cosmological principle; e.g., Rindler (1977), p. 203.) In particular, they can all start their clocks with the Big Bang.

Astronomers observe that the redshift z ident ( lambda - lambda ₀) / lambda ₀ of distant galaxies is proportional to their distance. We assume, for lack of any viable alternative explanation, that this redshift is due to the expansion of the universe. Recent evidence for this includes higher CBR temperature at higher redshift (Songaila et al. 1994b) and time dilation of high-redshift Type Ia supernovae (Goldhaber et al. 1996). 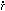The cosmological principle then implies (see, for example, Rowan-Robinson 1981, Section 4.3) that the expansion is homogeneous: r = a (t) r₀, which immediately implies Hubble's law: v = rdot = adot a^-1 r = H₀ r. Here r₀ is the present distance of some distant galaxy (the subscript ``0'' in cosmology denotes the present era), r is its distance as a function of time and v is its velocity, and a (t) is the scale factor of the expansion (scaled to be unity at the present: a (t₀) = 1). The scale factor is related to the redshift by a = (1 + z)^-1. Hubble's ``constant'' H(t) (constant in space, but a function of time except in an empty universe) is H(t) = adot a^-1.

Finally, it can be shown (see, e.g., Weinberg 1972, Rindler 1977) that the most general metric satisfying the cosmological principle is the Robertson-Walker metric

Equation 1.1 (1.1)

where the curvature constant k, by a suitable choice of units for r, has the value 1, 0, or -1, depending on whether the universe is closed, flat, or open, respectively. For k = 1 the spatial universe can be regarded as the surface of a sphere of radius a (t) in four-dimensional Euclidean space; and although for k = 0 or -1 no such simple geometric interpretation is possible, a (t) still sets the scale of the geometry of space.

Table 1.2. Theoretical Framework: GR Cosmology

Formally, GR consists of the assumption of the Equivalence Principle (or the Principle of General Covariance) together with Einstein's field equations, labeled (E) in Table 1.2, where the key equations have been collected. The Equivalence Principle implies that spacetime is locally Minkowskian and globally (pseudo-)Riemannian, and the field equations specify precisely how spacetime responds to its contents. The essential physical idea underlying GR is that spacetime is not just an arena, but rather an active participant in the dynamics, as summarized by John Wheeler: ``Matter tells space how to curve, curved space tells matter how to move.''

Comoving coordinates are coordinates with respect to which comoving observers are at rest. A comoving coordinate system expands with the Hubble expansion. It is convenient to specify linear dimensions in comoving coordinates scaled to the present; for example, if we say that two objects were 1 Mpc apart in comoving coordinates at a redshift of z = 9, their actual distance then was 0.1 Mpc. In a non-empty universe with vanishing cosmological constant, the case first studied in detail by the Russian cosmologist Alexander Friedmann in 1922-24, gravitational attraction ensures that the expansion rate is always decreasing. As a result, the Hubble radius R_H(t) ident c H(t)^-1 is increasing. The Hubble radius of a non-empty Friedmann universe expands even in comoving coordinates. Our backward lightcone encompasses more of the universe as time goes on.