© CAMBRIDGE UNIVERSITY PRESS 1999

1.3 Age, Expansion Rate, and Cosmological Constant

1.3.1 Age of the Universe t₀

The strongest lower limits for t₀ come from studies of the stellar populations of globular clusters (GCs). Standard estimates of the ages of the oldest GCs are t_GC 15-16 Gyr (Bolte & Hogan 1995; VandenBerg, Bolte, & Stetson 1996; Chaboyer et al. 1996). A frequently quoted lower limit on the age of GCs is 12 Gyr (Chaboyer et al. 1996), which is then an even more conservative lower limit on t₀ = t_GC + t_GC, where t_GC 0.5 Gyr is the time from the Big Bang until GC formation. The main uncertainty in the GC age estimates comes from the uncertain distance to the GCs: a 0.25 magnitude error in the distance modulus translates to a 22% error in the derived cluster age (Chaboyer 1995). (We will come back to this in the next paragraph.) All the other obvious ways to lower the calculated t_GC have been considered and found to have limited effects, and many non-obvious ideas have also been explored (VandenBerg et al. 1996). For example, stellar mass loss is a way of lowering t_GC (Willson, Bowen, & Struck-Marcell 1987), but observations constrain the reduction in t₀ to be less than ~ 1 Gyr (Shi 1995, Swenson 1995). Helium sedimentation during the main sequence lifetime can reduce stellar ages by ~ 1 Gyr (Chaboyer & Kim 1995, D'Antona et al. 1997). Note that the higher primordial ⁴He abundance implied by the new D/H (Deuterium/Hydrogen) values (Tytler, Burles & Kirkman 1996; Tytler, Fan & Burles 1996) lowers the central value of the GC ages by perhaps 0.5 Gyr (cf. Chaboyer 1995, Castellani et al. 1997). The usual conclusion has been that t₀ 12 Gyr is probably the lowest plausible value for t₀, obtained by pushing many but not all the parameters to their limits.

However, in March and April 1997, preliminary reports of analyses of data from the Hipparcos astrometric satellite have indicated that the distances to GCs assumed in obtaining the ages just discussed were systematically underestimated. If this is true, it follows that their stars at the main sequence turnoff are brighter and therefore younger. Indeed, there are indications that this correction will be largest for the lowest-metallicity clusters that had the oldest ages according to the standard analysis, according to Reid (1977). His analysis, using a sample including 15 metal-poor stars with parallaxes determined to better than 12% accuracy to redefine the subdwarf main sequence, gives distance moduli ~ 0.3 magnitudes (~ 30%) brighter than current standard values for his four lowest-metallicity GCs (M13, M15, M30, and M92), and ages (not lower limits) of ~ 12 Gyr. The shapes of the theoretical isochrones (Bergbusch & Vandenberg 1992) used in previous GC age estimates (e.g., Bolte & Hogan 1995, Sandquist et al. 1996) are no longer acceptable fits to the subdwarf data with the revised distances, although the isochrones of D'Antona et al. (1997) give better fits to the local subdwarfs and to the GCs. Another analysis (Gratton et al. 1997) uses a sample including 11 low-metallicity non-binary subdwarf stars with Hipparcos parallaxes better than 10% and accurate metal abundances from high-resolution spectroscopy to determine the absolute location of the main sequence as a function of metallicity. They then derive ages for the old GCs (M13, M68, M92, NGC288, NGC6752, 47 Tuc) in their GC sample of 12.1^+1.2_-3.6 Gyr. Their ages are lower both because of their 0.2 mag brighter distance moduli and because of their better metal determinations of cluster and field stars.

There are systematic effects that must be taken into account in the accurate determination of t_GC, including metallicity dependence and reddening corrections, and various physical phenomena such as stellar convection and helium sedimentation whose inclusion could lower ages still further and perhaps also bring theoretical isochrones into better agreement with the GC observations. Thus, there may be a period during which additional data is sought and theoretical models are revised before a new consensus emerges regarding the GC ages. But it does appear that the older estimates t_GC 15-16 Gyr will be revised downward substantially.

Stellar age estimates are also relevant to another sort of argument for an old, low-density universe: observation of apparently old galaxies at moderately high redshift (Dunlop et al. 1996). In the most extreme example presented so far (Spinrad et al. 1997), galaxy LDBS 53W091 at redshift z = 1.55 has a rest-frame spectrum very similar to that of an F6 star, and the claimed minimum age of 3.5 Gyr is based on standard stellar evolution models and assumptions about stellar populations, reddening, etc. The authors point out that for 3.5 Gyr to have elapsed at z = 1.55 requires h < 0.45 for = 1. (Note, however, that for 3.0 Gyr to have elapsed by z = 1.55 in an = 1 cosmology imposes the less restrictive requirement h < 0.53, for example.) Observations of old galaxies at high redshift will certainly constrain cosmological parameters, especially if the assumptions that go into the analysis can be independently verified.

Stellar age estimates are of course based on standard stellar evolution calculations. But the solar neutrino problem reminds us that we are not really sure that we understand how even our nearest star operates; and the sun plays an important role in calibrating stellar evolution, since it is the only star whose age we know independently (from radioactive dating of early solar system material). An important check on stellar ages can come from observations of white dwarfs in globular and open clusters (cf. Richer et al. 1995). And the two detached eclipsing binaries at the main sequence turn-off point recently discovered in Omega Centauri can be used both to measure the distance to this globular cluster accurately, and to determine their ages using the mass-luminosity relation (Paczynski 1996).

What if the GC age estimates are wrong for some unknown reason? The only other non-cosmological estimates of the age of the universe come from nuclear cosmochronometry - radioactive decay and chemical evolution of the Galaxy - and white dwarf cooling. Cosmochronometry age estimates are sensitive to a number of uncertain issues such as the formation history of the disk and its stars, and possible actinide destruction in stars (Malaney, Mathews, & Dearborn 1989; Mathews & Schramm 1993). However, an independent cosmochronometry age estimate of 13.8 ± 3.7 Gyr has been obtained for a single ultra-low-metallicity star ([Fe/H] = -3.1), based on the measured depletion of thorium (whose half-life is 14.2 Gyr) compared to stable heavy r-process elements (Cowan et al. 1997; cf. Bolte 1997, Sneden et al. 1996). This method will become very important if it is possible to obtain accurate measurements of r-process elements for a number of very low metallicity stars, and the resulting age estimates are consistent.

Independent age estimates come from the cooling of white dwarfs in the neighborhood of the sun. The key observation is that there is a lower limit to the luminosity, and therefore also the temperature, of nearby white dwarfs; although dimmer ones could have been seen, none have been found. The only plausible explanation is that the white dwarfs have not had sufficient time to cool to lower temperatures, which initially led to an estimate of 9.3 ± 2 Gyr for the age of the Galactic disk (Winget et al. 1987). Since there was evidence (based on the pre-Hipparcos GC distances) that the stellar disk of our Galaxy is about 2 Gyr younger than the oldest GCs (e.g., Stetson, VandenBerg, & Bolte 1996), this in turn gave an estimate of the age of the universe of t₀ ~ 11 ± 2 Gyr. More recent analyses (cf. Wood 1992, Hernanz et al. 1994) conclude that sensitivity to disk star formation history, and to effects on the white dwarf cooling rates due to C/O separation at crystallization and possible presence of trace elements such as ²²Ne, allow a rather wide range of ages for the disk of about 10 ± 4 Gyr. The latest determination of the white dwarf luminosity function, using white dwarfs in proper motion binaries, leads to a somewhat lower minimum luminosity and therefore a somewhat higher estimate of the age of the disk of ~ 10.5^+2.5_-1.5 Gyr (Oswalt et al. 1996).

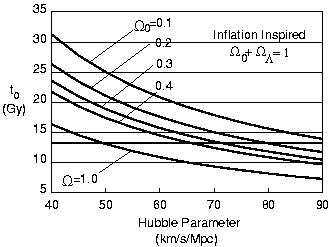
Figure 1.2. Age of the universe t0 as a function of Hubble parameter H0 in inflation inspired models with 0 + = 1, for several values of the present-epoch cosmological density parameter 0.

Suppose that the old GC stellar age estimates that t₀ 13 Gyr are right, as we will assume in much of the rest of this chapter. Figure 1.2 shows that t₀ > 13 Gyr implies that h 0.50 for = 1, and that h 0.73 even for ₀ as small as 0.3 in flat cosmologies (i.e., with ₀ + = 1). However, in view of the preliminary analyses using the new Hipparcos parallaxes and other new data that give strikingly lower age estimates for the oldest GCs, we should bear in mind that t₀ might actually be as low as ~ 11 Gyr, which would allow h as high as 0.6 for = 1.