

© CAMBRIDGE UNIVERSITY PRESS 1999
| |
1.5.2.2 Supersymmetric WIMPs
From the 1930s through the early 1970s, much of the development of quantum physics was a search for ever bigger symmetries, from spin and isospin to the Poincaré group, and from electroweak symmetry to grand unified theories (GUTs). The larger the symmetry group, the wider the scope of the connections established between different elementary particles or other quantum states. The basic pattern of progress was to find the right Lie group and understand its role - SU(2) as the group connecting different states in the cases of spin and isospin; SU(3) x SU(2) x U(1) as the dynamical gauge symmetry group of the ``Standard Model'' of particle physics, connecting states without a gauge boson to states of the same particles including a gauge boson. Supersymmetry is a generalization of this idea of symmetry, since it mixes space-time symmetries, whose quantum numbers include the spin of elementary particles, with internal symmetries. It is based on a generalization of Lie algebra called graded Lie algebra, which involves anti-commutators as well as commutators of the operators that transform one particle state into another. Supersymmetry underlies almost all new ideas in particle physics since the mid-1970s, including superstrings. If valid, it is also bound to be relevant to cosmology. (Some reviews: Collins, Martin, & Squires 1989; de Boer 1994.)
The simplest version of supersymmetry, which should be manifest at the GUT scale (~ 1016 GeV) and below, has as its key prediction that for every kind of particle that we have learned about at the relatively low energies which even our largest particle accelerators can reach, there should be an as-yet-undiscovered ``supersymmetric partner particle'' with the same quantum numbers and interactions except that the spin of this hypothetical partner particle differs from that of the known particle by half a unit. For example, the partner of the photon (spin 1) is the ``photino'' (spin 1/2), and the partner of the electron (spin 1/2) is the ``selectron'' (spin 0). Note that if a particle is a fermion (spin 1/2 or 3/2, obeying the Pauli exclusion principle), its partner particle is a boson (spin 0, 1, 2). The familiar elementary particles of matter (quarks and leptons) are all fermions, a fact that is responsible for the stability of matter, and the force particles are all bosons. Table 1.4 is a chart of the known families of elementary particles and their supersymmetric partners. It is these hypothetical partner particles among which we can search for the cold dark matter particle. The most interesting candidates are underlined. (As has already been mentioned, the gravitino is a warm dark matter particle candidate; this is discussed further below.)
| A hypothetical symmetry between boson and fermion fields and interactions | |||||||||||||||||||||||||||||
| Spin | Matter | Forces | Hypothetical superpartners | Spin | |||||||||||||||||||||||||
| (fermions) | (bosons) | ||||||||||||||||||||||||||||
| 2 | graviton | gravitino | 3/2 | ||||||||||||||||||||||||||
| 1 | photon, W±, Z0 | photino, winos, zino | 1/2 | ||||||||||||||||||||||||||
| gluons | gluinos | ||||||||||||||||||||||||||||
| 1/2 | quarks u,d, ... | 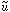 , , 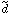 , ... , ...
0
|
| leptons e, |  e,
... e,
...
| 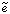 , ,
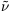 e, ... e, ...
| 0 | | Higgs bosons | Higgsinos | 1/2
| | | axion | axinos |
| Note: Supersymmetric cold dark matter candidate particles are
underlined.
| | |||||||||||
Note the parallel with Dirac's linking of special relativity and quantum mechanics in his equation for spin-1/2 particles (Griest 1996). In modern language, the resulting CPT invariance (under the combination of charge-conjugation C, replacing each particle with its antiparticle; parity P, reversing the direction of each spatial coordinate; and time-reversal T) requires a doubling of the number of states: an anti-particle for every particle (except for particles, like the photon, which are their own antiparticles).
There are two other key features of supersymmetry that make it
especially relevant to dark matter, R-parity and the connection
between supersymmetry breaking and the electroweak scale. The
R-parity of any particle is R  (-1)L+3B+2S,
where L, B, and S are its lepton number, baryon
number, and spin. Thus for
an electron (L = 1, B = 0, S = 1/2) R = 1,
and the same is true for
a quark (L = 0, B = 1/3, S = 1/2) or a photon
(L = 0, B = 0,
S = 1). Indeed R = 1 for all the known particles. But for a
selectron (L = 1, B = 0, S = 1/2) or a photino
(L = 0, B = 0,
S = 1/2), the R-parity is -1, or ``odd''. In most versions of
supersymmetry, R-parity is exactly conserved. This has the powerful
consequence that the lightest R-odd particle - often called the
``lightest supersymmetric partner'' (LSP) - must be stable, for
there is no lighter R-odd particle for it to decay into. The LSP is
thus a natural candidate to be the dark matter, as was first pointed
out by
Pagels & Primack
(1982),
although as mentioned above the LSP in
the early form of supersymmetry that we considered would have been a
gravitino weighing about a keV, which would now be classified as warm
dark matter.
(-1)L+3B+2S,
where L, B, and S are its lepton number, baryon
number, and spin. Thus for
an electron (L = 1, B = 0, S = 1/2) R = 1,
and the same is true for
a quark (L = 0, B = 1/3, S = 1/2) or a photon
(L = 0, B = 0,
S = 1). Indeed R = 1 for all the known particles. But for a
selectron (L = 1, B = 0, S = 1/2) or a photino
(L = 0, B = 0,
S = 1/2), the R-parity is -1, or ``odd''. In most versions of
supersymmetry, R-parity is exactly conserved. This has the powerful
consequence that the lightest R-odd particle - often called the
``lightest supersymmetric partner'' (LSP) - must be stable, for
there is no lighter R-odd particle for it to decay into. The LSP is
thus a natural candidate to be the dark matter, as was first pointed
out by
Pagels & Primack
(1982),
although as mentioned above the LSP in
the early form of supersymmetry that we considered would have been a
gravitino weighing about a keV, which would now be classified as warm
dark matter.
In the now-standard version of supersymmetry, there is an answer to
the deep puzzle why there should be such a large difference in mass
between the GUT scale MGUT ~ 1016 GeV and the
electroweak scale MEW = 80 GeV. Since both gauge
symmetries are
supposed to be broken by Higgs bosons which moreover must interact
with each other, the natural expectation would be that MGUT
~ MEW. The supersymmetric answer to this ``gauge hierarchy''
problem is that the masses of the weak bosons W±
and all other
light particles are zero until supersymmetry itself breaks. Thus,
there is a close relationship between the masses of the supersymmetric
partner particles and the electroweak scale. Since the abundance of
the LSP is determined by its annihilation in the early universe, and
the corresponding cross section involves exchanges of weak bosons or
supersymmetric partner particles - all of which have
electromagnetic-strength couplings and masses ~ MEW -
the cross
sections will be  ~
e2 s / MEW4 (where
s is the square of
the center-of-mass energy) i.e., comparable to typical weak
interactions. This in turn has the remarkable consequence that the
resulting density of LSPs today corresponds to nearly critical
density, i.e.
~
e2 s / MEW4 (where
s is the square of
the center-of-mass energy) i.e., comparable to typical weak
interactions. This in turn has the remarkable consequence that the
resulting density of LSPs today corresponds to nearly critical
density, i.e.  LSP ~ 1.
The LSP is typically a
spin-1/2 particle called a ``neutralino'' which is its own
antiparticle - that is, it is a linear combination of the photino
(supersymmetric partner of the photon), ``zino'' (partner of the
Z0
weak boson), ``Higgsinos'' (partners of the two Higgs bosons
associated with electroweak symmetry breaking in supersymmetric
theories), and ``axinos'' (partners of the axion, if it exists). In
much of the parameter space, the neutralino
LSP ~ 1.
The LSP is typically a
spin-1/2 particle called a ``neutralino'' which is its own
antiparticle - that is, it is a linear combination of the photino
(supersymmetric partner of the photon), ``zino'' (partner of the
Z0
weak boson), ``Higgsinos'' (partners of the two Higgs bosons
associated with electroweak symmetry breaking in supersymmetric
theories), and ``axinos'' (partners of the axion, if it exists). In
much of the parameter space, the neutralino  is a ``bino,'' a
particular linear combination of the photino and zino. All of these
neutralino LSPs are WIMPs, weakly interacting massive particles.
Because of their large masses, several 10s to possibly 100s of GeV,
these supersymmetric WIMPs would be dark matter of the ``cold'' variety.
is a ``bino,'' a
particular linear combination of the photino and zino. All of these
neutralino LSPs are WIMPs, weakly interacting massive particles.
Because of their large masses, several 10s to possibly 100s of GeV,
these supersymmetric WIMPs would be dark matter of the ``cold'' variety.
Having explained why supersymmetry is likely to be relevant to cold dark matter, one should also briefly summarize why supersymmetry is so popular with modern particle physicists. The reasons are that it is not only beautiful, it is even perhaps likely to be true. The supersymmetric pairing between bosons and fermions results in a cancellation of the high-energy (or ``ultraviolet'') divergences due to internal loops in Feynman diagrams. It is this cancellation that allows supersymmetry to solve the gauge hierarchy problem (how can MGUT / MEW be so big), and perhaps also unify gravity with the other forces (``superunification,'' ``supergravity,'' ``superstrings''). The one prediction of supersymmetry (Georgi, Quinn, & Weinberg 1974) that has been verified so far is related to grand unification (Amaldi, de Boer, & Furstenau 1991). The way this is usually phrased today is that the three gauge couplings associated with the three parts of the standard model - the SU(3) ``color'' strong interactions, and the SU(2) x U(1) electroweak interactions - do not unify at any higher energy scale unless the effects of the supersymmetric partner particles are included in the calculation, and they do unify with the minimal set of partners (one partner for each of the known particles) as long as the partner particles all have masses not much higher than the electroweak scale MEW (which, as explained above, is expected if electroweak symmetry breaking is related to supersymmetry breaking).
The expectations for the LSP neutralino, including prospects for their detection in laboratory experiments and via cosmic rays, have recently been exhaustively reviewed (Jungman, Kamionkowski, & Griest 1996). Several ambitious laboratory search experiments for LSPs in the mass range of tens to hundreds of GeV are now in progress (e.g., Shutt et al. 1996), and within the next few years they will have adequate sensitivity to probe a significant amount of the supersymmetric model parameter space. There are also hints of supersymmetric effects from recent experiments, which suggest that supersymmetry may be definitively detected in the near future as collider energy is increased - and also hint that the LSP may be rather light (Kane & Wells 1996), possibly even favoring the gravitino as the LSP (Dimopoulos et al. 1996).