

© CAMBRIDGE UNIVERSITY PRESS 1999
| |
1.6. Origin of Fluctuations: Inflation and Topological Defects
1.6.1 Topological defects
A fundamental scalar field, the Higgs field, is invoked by
particle theorists to account for the generation of mass;
one of the main goals of the next generation of particle
accelerators, including the Large Hadron Collider at CERN,
will be to verify the Higgs theory for the generation
of the mass of the weak vector bosons and all the lighter
elementary particles. Another scalar field is required to
produce the vacuum energy which may drive cosmic inflation
(discussed in the next section). Scalar fields can also
create topological defects that might be of great importance
in cosmology. The basic idea is that some symmetry is
broken wherever a given scalar field  has a non-vanishing value, so the dimensionality of the
corresponding topological defect depends on the number of
components of the scalar field: for a single-component real
scalar field,
has a non-vanishing value, so the dimensionality of the
corresponding topological defect depends on the number of
components of the scalar field: for a single-component real
scalar field,  (
(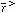 ) = 0 defines a two-dimensional
surface in three-dimensional space, a domain wall; for
a complex scalar field, the real and imaginary parts of
) = 0 defines a two-dimensional
surface in three-dimensional space, a domain wall; for
a complex scalar field, the real and imaginary parts of
 (
(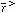 ) = 0 define a one-dimensional locus, a
cosmic string; for a three-component (e.g., isovector)
field,
) = 0 define a one-dimensional locus, a
cosmic string; for a three-component (e.g., isovector)
field,  i(
i(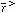 ) = 0 for i = 1, 2, 3 is satisfied at
isolated points, monopoles; for more than three
components, one gets textures that are not
topologically stable but which can seed structure in the
universe as they unwind.
) = 0 for i = 1, 2, 3 is satisfied at
isolated points, monopoles; for more than three
components, one gets textures that are not
topologically stable but which can seed structure in the
universe as they unwind.
To see how this works in more detail, consider a cosmic string. For
the underlying field theory to permit cosmic strings, we need to
couple a complex scalar field  to a
single-component (i.e.,
U(1)) gauge field A
to a
single-component (i.e.,
U(1)) gauge field A , like the electromagnetic field, in the
usual way via the substitution ð
, like the electromagnetic field, in the
usual way via the substitution ð -> D
-> D
 (ð
(ð - ie A
- ie A ), so that the scalar field
derivative term in the Lagrangian becomes
), so that the scalar field
derivative term in the Lagrangian becomes 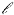 D
D =
|D
=
|D
 |2. Then if the scalar field
|2. Then if the scalar field
 gets a non-zero
value by the usual Higgs ``spontaneous symmetry breaking'' mechanism,
the gauge symmetry is broken because the field has a definite complex
phase. But along a string where
gets a non-zero
value by the usual Higgs ``spontaneous symmetry breaking'' mechanism,
the gauge symmetry is broken because the field has a definite complex
phase. But along a string where  =
0 the symmetry is restored.
As one circles around the string at any point on it, the complex phase
of
=
0 the symmetry is restored.
As one circles around the string at any point on it, the complex phase
of  (
(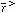 ) in general makes one,
or possibly n > 1, complete
circles 0 -> 2 n
) in general makes one,
or possibly n > 1, complete
circles 0 -> 2 n  . But since
such a phase rotation can
be removed at large distance from the string by a gauge transformation
of
. But since
such a phase rotation can
be removed at large distance from the string by a gauge transformation
of  and A
and A , the energy density
associated with this
behavior of
, the energy density
associated with this
behavior of 
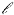 D
D -> 0 at large
distances, and therefore the energy µ per unit length of string is
finite. Since it would require an infinite amount of energy to unwind
the phase of
-> 0 at large
distances, and therefore the energy µ per unit length of string is
finite. Since it would require an infinite amount of energy to unwind
the phase of  at infinity, however,
the string is topologically
stable. If the field theory describing the early universe includes a
U(1) gauge field and associated complex Higgs field
at infinity, however,
the string is topologically
stable. If the field theory describing the early universe includes a
U(1) gauge field and associated complex Higgs field  , a rather
high density of such cosmic strings will form when the string field
, a rather
high density of such cosmic strings will form when the string field
 acquires its nonzero value and
breaks the U(1) symmetry. This
happens because there is no way for the phase of
acquires its nonzero value and
breaks the U(1) symmetry. This
happens because there is no way for the phase of  to be aligned
in causally disconnected regions, and it is geometrically fairly
likely that the phases will actually wrap around as required for a
string to go through a given region
(Kibble 1976).
The string network
will then evolve and can help cause formation of structure after the
universe becomes matter dominated, as long as the string density is
not diluted by a subsequent period of cosmic inflation (on the
difficult problem of combining cosmic defects and inflation, see,
e.g., Hodges &
Primack 1991).
A similar discussion can be given for
domain walls and local (gauge) monopoles, but these objects are
cosmologically pathological since they dominate the energy density and
``overclose'' the universe. But cosmic strings, a sufficiently low
density of global (i.e., non-gauged monopoles), and global textures
are potentially interesting for cosmology (recent reviews include
Vilenkin &
Shellard 1994,
Hindmarsh & Kibble
1995,
Shellard 1996).
Cosmic defects are the most important class of models producing
non-Gaussian fluctuations which could seed cosmic structure formation.
Since they are geometrically extended objects, they correspond to
non-local non-Gaussian fluctuations
(Kofman et al. 1991).
to be aligned
in causally disconnected regions, and it is geometrically fairly
likely that the phases will actually wrap around as required for a
string to go through a given region
(Kibble 1976).
The string network
will then evolve and can help cause formation of structure after the
universe becomes matter dominated, as long as the string density is
not diluted by a subsequent period of cosmic inflation (on the
difficult problem of combining cosmic defects and inflation, see,
e.g., Hodges &
Primack 1991).
A similar discussion can be given for
domain walls and local (gauge) monopoles, but these objects are
cosmologically pathological since they dominate the energy density and
``overclose'' the universe. But cosmic strings, a sufficiently low
density of global (i.e., non-gauged monopoles), and global textures
are potentially interesting for cosmology (recent reviews include
Vilenkin &
Shellard 1994,
Hindmarsh & Kibble
1995,
Shellard 1996).
Cosmic defects are the most important class of models producing
non-Gaussian fluctuations which could seed cosmic structure formation.
Since they are geometrically extended objects, they correspond to
non-local non-Gaussian fluctuations
(Kofman et al. 1991).
The parameter µ, usually quoted in the dimensionless
form Gµ (where G is Newton's constant), is the key
parameter of the theory of cosmic strings. The value
required for the COBE normalization is Gµ6
 Gµ
x 106 = 1-2 (recent determinations include
Gµ6 = 1.7 ± 0.7,
Perivolaropoulos
1993; 2,
Coulson et al. 1994;
(1.05-0.20+0.35),
Allen et al. 1996; 1.7,
Allen et al. 1997).
This is close enough to the value required for structure
formation, Gµ = (2.2-2.8) b8-1
x 10-6
(Albrecht &
Stebbins 1992),
with the smaller value for
cosmic strings plus cold dark matter and the higher value
for cosmic strings plus hot dark matter, so that the
necessary value of the biasing factor b8 is 1.3-3, which is
high (probably leading to underproduction of clusters, and
large-scale velocities that are low compared to observations
- cf.
Perivolaropoulos &
Vachaspati 1994),
but perhaps not
completely crazy. (Here b8 is the factor by which galaxies
must be more clustered than dark matter, on a scale of 8
h-1 Mpc.) Since generically Gµ ~ (M
/ mpl)2,
where M is the energy scale at which the string field
Gµ
x 106 = 1-2 (recent determinations include
Gµ6 = 1.7 ± 0.7,
Perivolaropoulos
1993; 2,
Coulson et al. 1994;
(1.05-0.20+0.35),
Allen et al. 1996; 1.7,
Allen et al. 1997).
This is close enough to the value required for structure
formation, Gµ = (2.2-2.8) b8-1
x 10-6
(Albrecht &
Stebbins 1992),
with the smaller value for
cosmic strings plus cold dark matter and the higher value
for cosmic strings plus hot dark matter, so that the
necessary value of the biasing factor b8 is 1.3-3, which is
high (probably leading to underproduction of clusters, and
large-scale velocities that are low compared to observations
- cf.
Perivolaropoulos &
Vachaspati 1994),
but perhaps not
completely crazy. (Here b8 is the factor by which galaxies
must be more clustered than dark matter, on a scale of 8
h-1 Mpc.) Since generically Gµ ~ (M
/ mpl)2,
where M is the energy scale at which the string field
 acquires its nonzero value, the
fact that Gµ ~
10-6, corresponding to M at roughly the Grand
Unification scale, is usually regarded as a plus for the
cosmic string scenario. (Even though there is no particular
necessity for cosmic strings in GUT scenarios, GUT groups
larger than the minimal SU(5) typically do contain the
needed extra U(1)s.) Moreover, the required normalization
is well below the upper limit obtained from the requirement
that the gravitational radiation generated by the evolution
of the string network not disrupt Big Bang Nucleosynthesis,
Gµ
acquires its nonzero value, the
fact that Gµ ~
10-6, corresponding to M at roughly the Grand
Unification scale, is usually regarded as a plus for the
cosmic string scenario. (Even though there is no particular
necessity for cosmic strings in GUT scenarios, GUT groups
larger than the minimal SU(5) typically do contain the
needed extra U(1)s.) Moreover, the required normalization
is well below the upper limit obtained from the requirement
that the gravitational radiation generated by the evolution
of the string network not disrupt Big Bang Nucleosynthesis,
Gµ  6 x
10-6. However, there is currently
controversy whether it is also below the upper limit from
pulsar timing, which has been determined to be Gµ
6 x
10-6. However, there is currently
controversy whether it is also below the upper limit from
pulsar timing, which has been determined to be Gµ  6 x 10-7
(Thorsett & Dewey
1996)
vs. Gµ
6 x 10-7
(Thorsett & Dewey
1996)
vs. Gµ  5
x 10-6
(McHugh et
al. 1996; cf.
Caldwell, Battye,
& Shellard 1996).
5
x 10-6
(McHugh et
al. 1996; cf.
Caldwell, Battye,
& Shellard 1996).
As for cosmic strings, the COBE normalization for global texture
models also implies a high bias b8  3.4 for h = 0.7
(Bennett & Rhie 1993),
although the needed bias is somewhat lower for
3.4 for h = 0.7
(Bennett & Rhie 1993),
although the needed bias is somewhat lower for 
 0.3
(Pen & Spergel 1995).
The latest global defect simulations
(Pen, Seljak, &
Turok, 1997)
show that the matter
power spectrum in all such models also has a shape very different
than that suggested by the available data on galaxies and clusters.
0.3
(Pen & Spergel 1995).
The latest global defect simulations
(Pen, Seljak, &
Turok, 1997)
show that the matter
power spectrum in all such models also has a shape very different
than that suggested by the available data on galaxies and clusters.
But both cosmic string and global defect models have a problem which
may be even more serious: they predict a small-angle CMB fluctuation
spectrum in which the first peak is at rather high angular wavenumber
 ~ 400
(Crittenden &
Turok 1995,
Durrer et al. 1996,
Magueijo et al. 1996)
and in any case is rather low in amplitude,
partly because of incoherent addition of scalar, vector, and tensor
modes, according to the latest simulations (strings:
Allen et al. 1997;
global defects:
Pen, Seljak, &
Turok 1997;
cf. Albrecht,
Battye, & Robinson 1997).
This is in conflict with the currently available
small-angle CMB data (Netterfield et al. 1997,
Scott et al. 1996),
which shows a peak at
~ 400
(Crittenden &
Turok 1995,
Durrer et al. 1996,
Magueijo et al. 1996)
and in any case is rather low in amplitude,
partly because of incoherent addition of scalar, vector, and tensor
modes, according to the latest simulations (strings:
Allen et al. 1997;
global defects:
Pen, Seljak, &
Turok 1997;
cf. Albrecht,
Battye, & Robinson 1997).
This is in conflict with the currently available
small-angle CMB data (Netterfield et al. 1997,
Scott et al. 1996),
which shows a peak at  ~ 250
and a drop at
~ 250
and a drop at 
 400,
as predicted by flat (
400,
as predicted by flat ( 0 +
0 + 
 = 1)
CDM-type models.
Since the small-angle CMB data is still rather preliminary, it is
premature to regard the cosmic defect models as being definitively
ruled out. It will be interesting to see the nature of the predicted
galaxy distribution and CMB anisotropies when more complete
simulations of cosmic defect models are run. This is more difficult
than simulating models with the usual inflationary fluctuations, both
because it is necessary to evolve the defects, and also because the
fact that these defects represent rare but high amplitude fluctuations
necessitates a careful treatment of their local effects on the
ordinary and dark matter. It may be difficult to sustain the effort
such calculations require, because the poor agreement between the
latest defect simulations and current small-angle CMB data does not
bode well for defect theories. Fortunately, there have been
significant technical breakthroughs in calculational techniques (cf.
Allen et al. 1997,
Pen et al. 1997).
= 1)
CDM-type models.
Since the small-angle CMB data is still rather preliminary, it is
premature to regard the cosmic defect models as being definitively
ruled out. It will be interesting to see the nature of the predicted
galaxy distribution and CMB anisotropies when more complete
simulations of cosmic defect models are run. This is more difficult
than simulating models with the usual inflationary fluctuations, both
because it is necessary to evolve the defects, and also because the
fact that these defects represent rare but high amplitude fluctuations
necessitates a careful treatment of their local effects on the
ordinary and dark matter. It may be difficult to sustain the effort
such calculations require, because the poor agreement between the
latest defect simulations and current small-angle CMB data does not
bode well for defect theories. Fortunately, there have been
significant technical breakthroughs in calculational techniques (cf.
Allen et al. 1997,
Pen et al. 1997).