© CAMBRIDGE UNIVERSITY PRESS 1999

1.6.3 Inflation and the Origin of Fluctuations

Thus far, it has been sketched how inflation stretches, flattens, and smooths out the universe, thus greatly increasing the domain of initial conditions that could correspond to the universe that we observe today. But inflation also can explain the origin of the fluctuations necessary in the gravitional instability picture of galaxy and cluster formation. Recall that the very existence of these fluctuations is a problem in the standard Big Bang picture, since these fluctuations are much larger than the horizon at early times. How could they have arisen?

The answer in the inflationary universe scenario is that they arise from quantum fluctuations in the inflaton field whose vacuum energy drives inflation. The scalar fluctuations during the de Sitter phase are of the order of the Hawking temperature H / 2. Because of these fluctuations, there is a time spread t / during which different regions of the same size complete the transition to the Friedmann phase. The result is that the density fluctuations when a region of a particular size re-enters the horizon are equal to _H ( / )_H ~ t / t_H = H t (Guth & Pi 1982; see Linde 1990 for alternative approaches). The time spread t can be estimated from the equation of motion of (the free Klein-Gordon equation in an expanding universe): 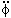+ 3H = -(ðV / ð ). 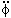Neglecting the term, since the scalar potential V must be very flat in order for enough inflation to occur (this is called the ``slow roll'' approximation), -V'/(3H), so <sub>H</sub> ~ H<sup>3</sup> / V' ~ V<sup>3/2</sup> / V'. Unless there is a special feature in the potential V() as rolls through the scales of importance in cosmology (producing such ``designer inflation'' features generally requires fine tuning - see e.g. Hodges et al. 1990), V and V' will hardly vary there and hence _H will be essentially constant. These are fluctuations of all the contents of the universe, so they are adiabatic fluctuations.

Thus inflationary models typically predict a nearly constant curvature spectrum _H = constant of adiabatic fluctuations. Some time ago Harrison (1970), Zel'dovich (1972), and others had emphasized that this is the only scale-invariant (i.e., power-law) fluctuation spectrum that avoids trouble at both large and small scales. If _H M_H^-, where M_H is the mass inside the horizon, then if - is too large the universe will be less homogeneous on large than small scales, contrary to observation; and if is too large, fluctuations on sufficiently small scales will enter the horizon with _H >> 1 and collapse to black holes (see e.g. Carr, Gilbert, & Lidsey 1995, Bullock & Primack 1997); thus 0. The = 0 case has come to be known as the Zel'dovich spectrum.

Inflation predicts more: it allows the calculation of the value of the constant _H in terms of the properties of the scalar potential V(). Indeed, this proved to be embarrassing, at least initially, since the Coleman-Weinberg potential, the first potential studied in the context of the new inflation scenario, results in _H ~ 10² (Guth & Pi 1982) some six orders of magnitude too large. But this does not seem to be an insurmountable difficulty; as was mentioned above, chaotic inflation works, with a sufficiently small self-coupling. Thus inflation at present appears to be a plausible solution to the problem of providing reasonable cosmological initial conditions (although it sheds no light at all on the fundamental question why the cosmological constant is so small now). Many variations of the basic idea of inflation have been worked out, and the following sections will discuss two recent developments in a little more detail. Linde (1995) recently classified these inflationary models in an interesting and useful way: see Table 1.7.

Table 1.7. Linde's Classification of Inflation Models