

© CAMBRIDGE UNIVERSITY PRESS 1999
| |
1.6.5 A Supersymmetric Inflation Model
We have already considered, in connection with cold dark matter candidates, why supersymmetry is likely to be a feature of the fundamental theory of the particle interactions, of which the present ``Standard Model'' is presumably just a low-energy approximation. If the higher-energy regime within which cosmological inflation occurs is described by a supersymmetric theory, there are new cosmological problems that initially seemed insuperable. But recent work has suggested that these problems can plausibly be overcome, and that supersymmetric inflation might also avoid the fine-tuning otherwise required to explain the small inflaton coupling corresponding to the COBE fluctuation amplitude. Here the problems will be briefly summarized, and an explanation will be given of how one such model, due to Ross & Sarkar (1996; hereafter RS96) overcomes them. (An interesting alternative supersymmetric approach to inflation is sketched in Dine et al. 1996.)
When Pagels and I
(1982)
first suggested that the lightest supersymmetric
partner particle (LSP), stable because of R-parity, might be the dark
matter particle, that particle was the gravitino in the early version of
supersymmetry then in fashion.
Weinberg (1982)
immediately pointed out
that if the gravitino were not the LSP, it could be a source or real
trouble because of its long lifetime ~
MPl2 / m3/23
~ (m3/2 / TeV)-3 103 s, a
consequence of its gravitational-strength
coupling to other fields. Subsequently, it was realized that
supersymmetric theories can naturally solve the gauge hierarchy problem,
explaining why the electroweak scale MEW ~
102 GeV is so much
smaller than the GUT or Planck scales. In this version of supersymmetry,
which has now become the standard one, the gravitino mass will typically
be m3/2 ~ TeV; and the late decay of even a relatively
small number
of such massive particles can wreck BBN and/or the thermal spectrum of
the CBR. The only way to prevent this is to make sure that the reheating
temperature after inflation is sufficiently low: TRH
 2
x 109 GeV (for m3/2 = TeV)
(Ellis, Kim, &
Nanopoulos 1984,
Ellis et al. 1992).
2
x 109 GeV (for m3/2 = TeV)
(Ellis, Kim, &
Nanopoulos 1984,
Ellis et al. 1992).
This can be realized in supergravity theories rather naturally
(RS96).
Define M  MPl / (8
MPl / (8  )1/2 = 2.4 x 1018
Gev. Break GUT by the Higgs field
)1/2 = 2.4 x 1018
Gev. Break GUT by the Higgs field  with vacuum expectation
value (vev) <
with vacuum expectation
value (vev) < > ~ 1016
GeV. Break supersymmetry by a
gaugino condensate <
> ~ 1016
GeV. Break supersymmetry by a
gaugino condensate <
 > ~ (1013
GeV)3;
then the gravitino mass is m3/2 ~ <
> ~ (1013
GeV)3;
then the gravitino mass is m3/2 ~ <
 > / M2 ~
TeV. Inflation is expected to inhibit such breaking, so it must occur
afterward. The inflaton superpotential has the form I =
> / M2 ~
TeV. Inflation is expected to inhibit such breaking, so it must occur
afterward. The inflaton superpotential has the form I =  2 M
f(
2 M
f( / M), with the
corresponding potential
/ M), with the
corresponding potential
with minimum at
(Holman, Raymond, & Ross 1984). This particular inflaton potential is
of the ``new inflation'' type, and corresponds to tilt
np = 0.92 and
a number of e-folds during inflation
assuming that the starting value of the inflaton field
Note the following features of the above scenario: inflation occurs at an
energy scale far below the GUT scale, so there is essentially no gravity
wave contribution to the large-angle CMB fluctuations (i.e., T / S
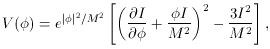
 0.
Demanding that at this minimum
the potential actually vanishes V(
0.
Demanding that at this minimum
the potential actually vanishes V( 0) = 0, i.e., that the
cosmological constant vanishes, implies that
I(
0) = 0, i.e., that the
cosmological constant vanishes, implies that
I( 0) =
(ðI / ð
0) =
(ðI / ð )
) 0 = 0. The
simplest possibility is I =
0 = 0. The
simplest possibility is I =  2 (
2 ( -
-  0)2 / M.
Requiring that ðV / ð
0)2 / M.
Requiring that ðV / ð |0 = 0 for a
sufficiently flat potential, implies that
|0 = 0 for a
sufficiently flat potential, implies that  0 = M and
that the second derivative also vanishes at the origin; thus
0 = M and
that the second derivative also vanishes at the origin; thus
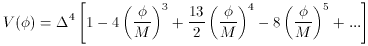
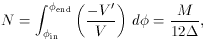
 in
is sufficiently close to the origin (which has relatively small but
nonvanishing probability - the
in
is sufficiently close to the origin (which has relatively small but
nonvanishing probability - the  field presumably has a broad
initial distribution). Matching The COBE fluctuation amplitude
requires that
field presumably has a broad
initial distribution). Matching The COBE fluctuation amplitude
requires that  / M = 1.4
x 10-4, which in turn implies that
N ~ 103, m
/ M = 1.4
x 10-4, which in turn implies that
N ~ 103, m ~
~  2 / M ~ 1011 GeV,
TRH
~ 105 GeV (parametric resonance reheating does not occur). Such
a low reheat temperature insures that there will be no gravitino
problem, and requires that the baryon asymmetry be generated by
electroweak baryogenesis - which appears to be viable as long as the
theory contains adequately large CP violation.
2 / M ~ 1011 GeV,
TRH
~ 105 GeV (parametric resonance reheating does not occur). Such
a low reheat temperature insures that there will be no gravitino
problem, and requires that the baryon asymmetry be generated by
electroweak baryogenesis - which appears to be viable as long as the
theory contains adequately large CP violation.
 0) even through there is
significant tilt (np = 0.92 for the
particular potential above); there is a low reheat temperature, so
electroweak baryogenesis is required; and the universe is predicted to be
very flat since there are many more e-folds than required to solve the
flatness problem.
0) even through there is
significant tilt (np = 0.92 for the
particular potential above); there is a low reheat temperature, so
electroweak baryogenesis is required; and the universe is predicted to be
very flat since there are many more e-folds than required to solve the
flatness problem.