11.2. Orbits in a Barred Galaxy

Knowledge of the stellar orbits in a barred galaxy can help us to understand the dynamical properties of bars, their extension, and pattern velocity. It is also fundamental to understanding resonances, the behavior of the gas component, and therefore to explaining the existence of rings.

Bars are three-dimensional components, and they can be modeled as triaxial ellipsoids. Although the disks of spiral galaxies are very thin components, with axis ratios around 10, bars can be thicker because of vertical resonances (e.g. Combes et al. 1990b), and reveal box or peanut shapes when seen edge-on. In a first approach, we will describe the stellar orbits as if they were confined in the galaxy plane. This much simpler approach gives already most of the characteristics of bar dynamics and is sufficient to understand the gas behavior, since the gas disk is much thinner.

First, let us recall the characteristics of orbits in an axisymmetric potential (r) in the plane z = 0. A circular orbit has an angular velocity ² = 1 / r d / dr. In linearizing the potential in the neighborhood of a circular orbit, the motion of any particle can be expressed in first order by an epicyclic oscillation, of frequency ,

² = d² / dr ² + 3 ² = r d ² / dr + 4 ² 6

The general orbit is therefore the combination of a circle and an epicycle, or a rosette, since there is no rational relation between the two periods.

The bar creates a bisymmetric gravitational potential, with a predominant Fourier component m = 2, which rotates in the galaxy with the pattern speed _b. To be left with a potential independent of time, where the energy of particles is conserved, we must consider the orbits in the rotating frame. The equivalent potential in this frame is then:

_eq = (r, ) - 1/ 2 _b² r² 7

in cylindrical coordinates (r, , z), for z = 0.

The energy of a particle (per unit mass) in this frame is

E_J = 1/ 2 v² + - 1/ 2 _b² r². 8

It is an integral called the Jacobi integral. It is expressed as a function of the energy in the fixed frame E, as E_J = E - _b L_z , where L_z is the angular momentum, which is not an integral, since the potential is non-axisymmetric.

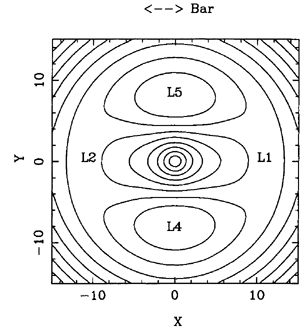
Figure 58. Equipotentials in the rotating frame of the bar. This picture already provides a good hint of some of the periodic orbit shapes.

The equipotentials in the rotating frame are given in Figure 58. There exist 5 stationary points, known as Lagrangian points, L₁ to L₅, where the derivative of _eq vanishes. L₃ is the central minimum, L₄ and L₅ are maxima, and L₁ and L₂ are saddle points. Only L₄ and L₅ are stable, i.e., a particle can oscillate around them with the epicyclic frequency. The four points, L₁, L₂, L₄, and L₅ correspond to the corotation resonance with the bar. Although they are not located at the same galactocentric distance, they delineate an annular zone, called the corotation zone.

Lindblad Resonances

In the rotating frame, the effective angular velocity of a particle is ' = - _b. There exists then regions in the galaxy where ' = / m, i.e. where the epicyclic orbits close themselves after m lobes. The corresponding stars are aligned with the perturbation and closely follow it; they interact with it always with the same sign, and resonate with it. These zones are the Lindblad resonances, sketched with dashed circles in Figure 59a. 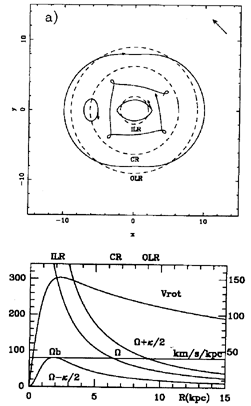According to the relative values of and in a realistic disk galaxy (Figure 59b), and because the bar is a bisymmetric perturbation, the most important resonances are those for m = 2. An obvious resonance is corotation, for which = _b (' = 0).

Figure 59. Lindblad resonances: a) resonant orbits in the rotating frame of the bar; b) rotation curve (left scale, km/s) and frequencies (right, km/s/kpc) used to model these orbits. The pattern speed of the bar is indicated.

The periodic orbits are numerous (see the recent review by Contopoulos & Grosbøl 1989), and we will describe here the most important ones for the bar support, and for the ring formation mechanism:

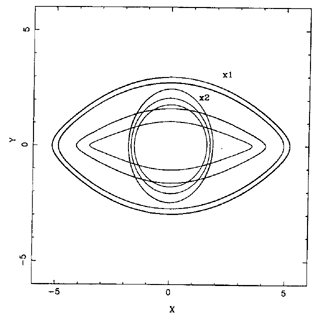
1. the x₁ family (see Figure 60) is the main family supporting the bar. Orbits are elongated parallel to the bar, within corotation. They can look like simple ellipses, and with energy increasing, they can form a cusp, and even two loops at the extremities.

   Figure 60. Shape of the main families of periodic orbits in a barred galaxy, (see e.g. Contopoulos & Papayannopoulos 1980). Some x₁ orbits parallel to the bar are represented, together with some x₂ perpendicular orbits, inside CR.

2. the x₂ family exists only between the two inner Lindblad resonances (ILR), when they exist. They are more round, and elongated perpendicular to the bar. In the same category of 2 / 1 orbits (which close after one turn and two epicycles), there are also the x₄ retrograde orbits, and the x₃ unstable orbits, but with less impact for galaxies. The presence or not of nuclear rings appears to be related to the existence of an ILR, as we have discussed in sections 9.7 and 9.8, and which will be developed later. Even when there exist two ILR's in the axisymmetric sense, the existence of the x₂ family is not certain. When the bar is strong enough, the x₂ orbits disappear. The bar strength necessary to eliminate the x₂ family depends on the pattern speed _b: the lower this speed, the stronger the bar must be.

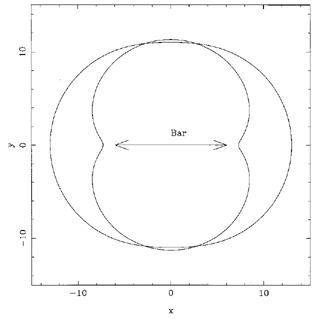
3. Outside corotation, the 2 / 1 orbits that are run in the retrograde sense in the rotating frame are perpendicular to the bar inside the outer Lindblad resonance (OLR), and parallel to the bar slightly outside (Figure 61). These orbits are also discussed by Kalnajs (1991). Their shape reveals a characteristic figure-eight, that is very similar to the dimpled shape of some outer rings in barred galaxies (see section 4.1 and Figure 18). When the bar is strong, most orbits perpendicular to the bar between CR and OLR become unstable. That is why this region is often depopulated and, in real galaxies, never includes recent star formation.

   Figure 61. Shape of the two main families of periodic orbits near the outer Lindblad resonance (OLR). The orbit inside OLR is perpendicular to the bar, while the orbits outside OLR are parallel. The first one displays the characteristic dimpling that corresponds to observations of R₁ outer rings.

4. When getting towards corotation (CR) all higher order resonances ' = / m with m 3 are encountered. Spanning this region, on the inner or outer side of CR, the periodic families 6 / 1 and 4 / 1 are displayed in Figure 62. The 4 / 1 resonant family is likely to play a role in the formation of inner rings.

   Figure 62. The 4 / 1 and 6 / 1 periodic orbits, from Contopoulos & Grosbøl (1989). The bar is vertical, and the circle indicates corotation.

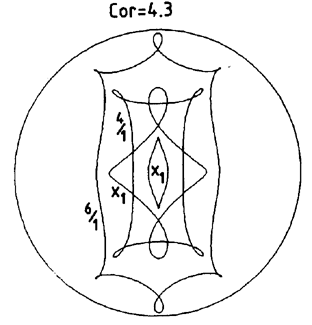
5. Finally, circulating around the Lagrangian points L₄ and L₅, one can distinguish the banana orbits or long period orbits (LPO), and the short period orbits (SPO).

The existence of a small zone between the two ILR's where the orbits are not supporting the bar helps to understand the decoupling of a second pattern, rotating faster than the main bar, in the nuclear parts of some barred spiral galaxies. Examples of this decoupling into two patterns can be found in the ``nuclear barred'' galaxies (e.g. de Vaucouleurs 1975a; Jarvis et al. 1988; Shaw et al. 1993; Buta & Crocker 1993). The nuclear bar often occurs inside the nuclear ring, corresponding to the ILR (see section 16).

Beyond corotation, the stable periodic orbits are also perpendicular to the bar, which suggests that a self-consistent bar cannot extend far beyond its own corotation. This has been verified in N-body simulations of barred galaxies (e.g., Sellwood 1981; Combes & Sanders 1981; Sparke & Sellwood 1987): the longest bars end just slightly before their corotation.

Approaching the corotation region, higher order resonances occur, and the periodic orbits become more and more complex and squarish. The observed shape of face-on early-type galaxy bars is indeed boxy, as was shown for NGC 936 by Kormendy (1983), which compares very well with N-body models (e.g. Miller & Smith 1979). This squarish shape might measure the importance of the 4 / 1 resonance, which will in turn have a strong consequence for inner rings encircling the bars.