|



9.8. Kinematic Studies
Kinematic studies of ringed galaxies have been concerned with rotation curves, global velocity fields, and specific ring velocity fields. These studies have revealed a great deal of heterogeneity in the dynamical properties of these galaxies.
Velocity Fields
One of the first kinematic studies of a ringed galaxy was made by van der Kruit (1974, 1976a, b), who mapped the velocity field of the very bright inner ring of NGC 4736 from optical emission lines seen in slit spectra. Evidence for noncircular motions was found on the southeast side of the ring, but little about the global velocity field could be deduced because of the faintness of any emission away from the ring. Bosma et al. (1977) later mapped the global HI velocity field of the galaxy, but these observations lacked sufficient resolution in the inner ring region. Another ringed galaxy which had early extensive kinematic studies was NGC 3351, an SB(r)-type spiral in the Leo Group (Rubin et al. 1975; Peterson et al. 1976). Emission line velocities were obtained for the inner and nuclear rings, and the outer arms, but the data were insufficient to plot a two-dimensional velocity field since the ionized gas was mostly confined to the two rings.
Buta (1984) obtained kinematic data for eight ringed galaxies over a range of types and bar strengths, and including NGC 3351 and 4736. The results were described in several papers (NGC 1433: Buta 1986b; NGC 7531: Buta 1987a; NGC 6300: Buta 1987b; NGC 1512, 3351, 4725, and 4736: Buta 1988). The velocity fields were derived from either slit spectroscopy or Fabry-Perot interferometry. The latter technique is especially good for giving more complete information on HII region distributions and velocity fields than slit spectra, and was used for NGC 1433, 1512, 3351, 4725, 4736, and 7531. In NGC 1433 and 1512, the velocity points detected were mainly associated with inner and nuclear rings. This localized nature of the HII region distribution precluded the construction of a serious dynamical model of these galaxies. In NGC 3351 and 4725, more HII regions were detected beyond the inner rings, but again, little emission was found between the center and the inner rings.

|
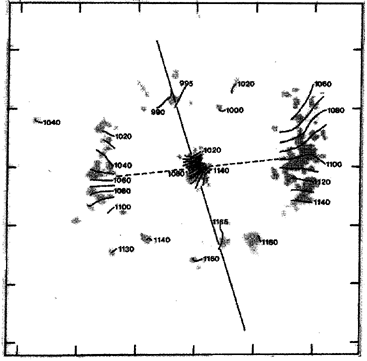
The velocity field of NGC 1433 is the most interesting of these early
ones studied because it immediately brings to light the possibility of
intrinsic oval shapes of inner SB rings and intrinsic bar and inner
ring alignment, aspects which had been suspected prior to 1964 by G. de
Vaucouleurs (see
Figure 7).
Kormendy (1979a)
had
alternatively deduced from a survey of a small number of barred spirals
that inner rings are nearly round, and NGC 1433 provided a clear-cut
test of either hypothesis. This galaxy's inner ring is highly
elongated nearly along the strong bar in projection. If this apparent
alignment were due purely to projection effects on a circular ring,
then the line of nodes should be along the ring major axis. However,
the observed velocity gradient is nearly perpendicular to this axis,
meaning that the ring is intrinsically aligned with the bar (see
Figure 50). A moderately high resolution HI velocity
field of NGC 1433, from
Ryder et al. (1996),
is shown in
Figure 51, and confirms the line of nodes previously
found from the Fabry-Perot interferometry.
Buta & Purcell
(1996) and
Buta, Lewis, and
Purcell (1996) have
obtained new H velocity
fields of five CSRG galaxies, NGC 3081,
IC 4214, IC 4290, ESO 509-98, and ESO 566-24, with the Rutgers
Fabry-Perot interferometer at Cerro Tololo Inter-American Observatory.
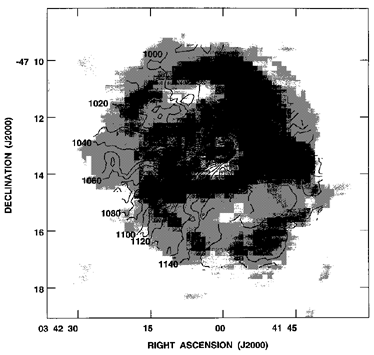
Figure 52 shows a color-coded radial velocity
map of NGC 3081. This demonstrates the presence of a
bounded zone of
ionized gas in an oval structure associated with the bright blue light
inner ring. The ring includes both discrete HII regions and diffuse
ionized gas. The situation is similar to what was found for NGC 4736 by
van der Kruit (1976b).
It is noteworthy that the inner edge of the
ionized gas zone is less oval in projected shape than the outer edge;
this was also seen in the shapes of isochromes of the ring in a B - I
color index map by
Buta (1990a).
The difference may reflect a changing
shape of the periodic orbits with radius in the galaxy plane.
velocity
fields of five CSRG galaxies, NGC 3081,
IC 4214, IC 4290, ESO 509-98, and ESO 566-24, with the Rutgers
Fabry-Perot interferometer at Cerro Tololo Inter-American Observatory.
Figure 52 shows a color-coded radial velocity
map of NGC 3081. This demonstrates the presence of a
bounded zone of
ionized gas in an oval structure associated with the bright blue light
inner ring. The ring includes both discrete HII regions and diffuse
ionized gas. The situation is similar to what was found for NGC 4736 by
van der Kruit (1976b).
It is noteworthy that the inner edge of the
ionized gas zone is less oval in projected shape than the outer edge;
this was also seen in the shapes of isochromes of the ring in a B - I
color index map by
Buta (1990a).
The difference may reflect a changing
shape of the periodic orbits with radius in the galaxy plane.
|
|
Rotation Curves
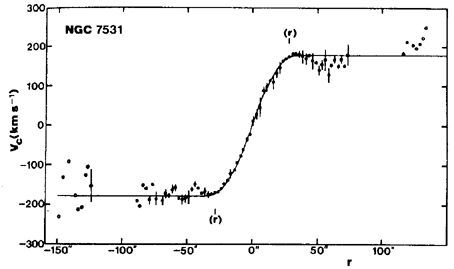
Optical rotation curves of ringed galaxies yield some curious coincidences. For example, in the weakly-barred spiral NGC 7531, the very bright inner ring lies virtually exactly at the turnover radius (Buta 1987a; see Figure 53). The same appears to be true for the nuclear rings of NGC 7217 (Peterson et al. 1978), NGC 1097 (Wolstencroft & Schempp 1979), NGC 5728 (Rubin 1980), NGC 1512 (Buta 1988), NGC 1068 (Telesco & Decher 1988), and ESO 565-11 (Buta et al. 1995a), and may be more generally true in the case of such rings as suggested by Kenney et al.(1993). The latter authors found that a starburst nuclear feature in NGC 3504 lies very close to turnover in a CO rotation curve. The inner ring of NGC 4736 lies well beyond turnover, however (van der Kruit 1976b; Buta 1988; Mulder 1994). We believe that the same will generally be true of most inner rings in SB galaxies. The nuclear rings of the SB galaxies studied lie well inside the bar, while the inner ring of NGC 7531 surrounds the weak bar in the system. The turnover coincidence of the inner ring of NGC 7531 and the nuclear rings of barred spirals is an important observation to be explained by dynamical models.
|
Another curious aspect of rings evident from rotation curves has to do
with the total mass in the rings. Two interesting cases are NGC 6300
and 7531. In NGC 6300, the spiral inner pseudoring
produces a large
hump in an azimuthally averaged luminosity profile. The ring is also
the location of a ``step'' in the rotation curve.
Buta (1987b)
transformed the light profile into a rotation curve (a ``maximum disk''
type solution) and found good agreement with the observed rotation
curve. It appears that in this case, the pseudoring has significant
self-gravity. Curiously,
Ryder et al. (1996)
observed NGC 6300 in HI,
but detected no hump in the ring region for a fixed inclination and
line of nodes solution. H rotation profiles at different position angles (also from
Buta 1987b)
show that the hump is not
uniformly strong with azimuth, and the feature may be smoothed over in
HI solutions.
rotation profiles at different position angles (also from
Buta 1987b)
show that the hump is not
uniformly strong with azimuth, and the feature may be smoothed over in
HI solutions.
Buta (1987a) showed, on the other hand, that a transformed I-band light profile of NGC 7531 produced a rotation curve in very poor agreement with the observed rotation curve. In this case, the light profile predicts a large hump near the ring which is not observed, and a Keplerian fall-off almost immediately outside the ring. Thus, the inner ring of NGC 7531, though conspicuous even in the I-band, may not contain a great deal of mass, or else the galaxy is dominated by dark matter even at these inner radii.
Rubin (1980) presented an interesting rotation curve for NGC 5728, a large southern barred spiral with all three ring types (CSRG type (R1)SAB(r,nr)a). Rubin noted an extreme mis-centering of the nuclear ring on the optical nucleus. The rotation curve showed a steep rise to maximum near the position of the nuclear ring, followed by an apparent decline in velocities and a subsequent rise in the region of an inner ring/lens zone. Rubin interpreted the peculiar rotation curve in terms of a two-component model consisting of a centrally condensed bulge and a constant density, uniformly rotating disk, and suggested that barred galaxies like NGC 5728 in general rotate with constant angular velocity. However, it is now known that any rotation curve derived for a barred spiral will be aspect-dependent (e.g., van Albada & Roberts 1981). Also, Rubin chose orientation parameters for NGC 5728 based on the appearance of the inner ring/lens zone, but it is clear now that this feature is intrinsically oval and misaligned with the true major axis of the galaxy by about 33° (Schommer et al. 1988).
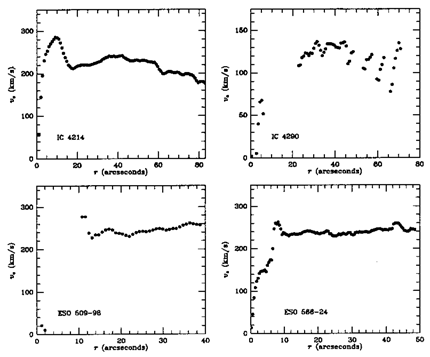
Figure 54 shows rotation curves for four CSRG
galaxies from
H Fabry-Perot
interferometry. The sample includes four
distinctive types of ringed systems: IC 4214: a tripled-ringed
weakly-barred galaxy; IC 4290, an SB(r)-type spiral with a very strong
inner ring; ESO 509-98, the prototype of the
R1R'2
subclass of outer features; and ESO 566-24, a very regular example of
a four-armed, ringed barred spiral. Blue light images of all four
galaxies are illustrated in
Buta & Crocker (1991).
In these cases
the ``normalcy'' of the rotation curves is noteworthy. There are humps
in the central regions of IC 4214 and ESO 566-24 due to rapid
rotation in the region of a nuclear ring. The rotation curve of IC 4290
is defined almost entirely by a slightly oval inner ring.
Fabry-Perot
interferometry. The sample includes four
distinctive types of ringed systems: IC 4214: a tripled-ringed
weakly-barred galaxy; IC 4290, an SB(r)-type spiral with a very strong
inner ring; ESO 509-98, the prototype of the
R1R'2
subclass of outer features; and ESO 566-24, a very regular example of
a four-armed, ringed barred spiral. Blue light images of all four
galaxies are illustrated in
Buta & Crocker (1991).
In these cases
the ``normalcy'' of the rotation curves is noteworthy. There are humps
in the central regions of IC 4214 and ESO 566-24 due to rapid
rotation in the region of a nuclear ring. The rotation curve of IC 4290
is defined almost entirely by a slightly oval inner ring.
|
Velocity-Position Angle Diagrams
The velocity-position angle diagram is a useful tool for characterizing
the motions within rings
(van der Kruit 1974).
Rings represent intense
zones of H emission in
some galaxies, and since little emission
may come from elsewhere in the disk, full dynamical models are usually
precluded. Ring velocity-position angle diagrams provide a means of
getting at dynamics in spite of the sparse amount of velocity
information because noncircular motions can be detected in such
diagrams.
emission in
some galaxies, and since little emission
may come from elsewhere in the disk, full dynamical models are usually
precluded. Ring velocity-position angle diagrams provide a means of
getting at dynamics in spite of the sparse amount of velocity
information because noncircular motions can be detected in such
diagrams.
The work of van der Kruit (1974) on NGC 4736 suggested that noncircular motions in rings could be detected either as shifts of the apparent line of nodes or as asymmetries in the velocity-position angle diagram. Various ways of modeling the diagram include pure circular rotation, rotation plus expansion or contraction, resonance dispersion orbits, and uniformly precessing elliptical orbits. These kinds of models can fit the velocity-position angle diagrams of rings very well in some cases, but do not provide the most reliable interpretation of the dynamics.
An inner Lindblad resonance dispersion orbit
(Lindblad 1955;
Lindblad &
Jörsäter 1981)
is an ordinary unperturbed galactic orbit which
appears closed in a reference frame rotating at an angular velocity
 p =
p =
 -
-  / 2
/ 2 = mean circular angular
velocity;
= mean circular angular
velocity;  = epicyclic
frequency).
Lin (1971) and
Mark (1974a)
had long ago suggested that inner rings of ionized gas and young stars
could develop at this resonance, where the spiral density
``wavelength'' approaches zero (see also
Lindblad 1974).
The mass in
the dispersion orbit is assumed to be small and not in itself capable
of influencing the dynamics of the galaxy. A resonance dispersion orbit
provided a popular interpretation of the ``3 kpc'' arm in the Galaxy
(Rougoor & Oort 1960)
in several early papers (e. g.,
Shane 1972;
Simonson & Mader 1973)
and in M51
(Tully 1974).
= epicyclic
frequency).
Lin (1971) and
Mark (1974a)
had long ago suggested that inner rings of ionized gas and young stars
could develop at this resonance, where the spiral density
``wavelength'' approaches zero (see also
Lindblad 1974).
The mass in
the dispersion orbit is assumed to be small and not in itself capable
of influencing the dynamics of the galaxy. A resonance dispersion orbit
provided a popular interpretation of the ``3 kpc'' arm in the Galaxy
(Rougoor & Oort 1960)
in several early papers (e. g.,
Shane 1972;
Simonson & Mader 1973)
and in M51
(Tully 1974).
A uniformly precessing ellipse model is an approximation to an orbit in a bar-perturbed potential. The precession rate would be the same as the bar pattern speed, and hence such a model allows an estimate of the bar pattern speed from a velocity-position angle diagram. The equations of such a model were derived from the solution to the equations of motion for a uniformly rotating disk (Chevalier & Furenlid 1978). A variation on this model which expresses radial and tangential velocity components as sinusoidal functions of azimuth around the ring was used by Buta (1986b, 1988).
Van der Kruit (1974) analyzed the velocity-position angle diagram of the inner ring of NGC 4736 in terms of uniform circular rotation and uniform circular rotation with uniform radial expansion or contraction. In order to match the kinematic line of nodes with the observed major axis position angle of the ring, van der Kruit deduced that the ring must be expanding as well as rotating. The expansion velocity required was about 30 km s-1. The radial term does not lead to an asymmetry in the velocity-position angle diagram, but shifts the apparent line of nodes by nearly 10°, owing to the fairly low inclination of 35°. A resonance dispersion orbit was also tried but found not to represent the observed velocity-position angle diagram.
The velocity-position angle diagrams of the inner and nuclear rings of NGC 3351 were analyzed by Rubin et al. (1975) and Peterson et al. (1976). In this case, the velocities in the inner ring were found to be consistent with circular motions, but those in the nuclear ring could be interpreted in terms of rotation plus a uniform contraction of 34 km s-1. A precessing elliptical orbit was also tried for the nuclear ring and found to represent the data as well as a contracting ring model.
Meaburn et al. (1981) studied the motions within the nuclear pseudoring of NGC 1097. Complex line profiles with multiple components were detected. The velocity-position angle diagram of the ring was analyzed in terms of circular motions, with the multiple components possibly due to different spirals in different planes or having different rotational velocities.
The problem with these early interpretations is that the results are
very sensitive to the adopted orientation parameters of the parent galaxy.
Buta (1988)
presented a new analysis of the velocity field of
the inner ring of NGC 4736 based on a combination of H Fabry-Perot interferometry data and the slit spectroscopy of
van der Kruit (1976a).
Models of pure circular rotation, rotation plus
expansion, and a resonance dispersion orbit fit the data equally well
with required line of nodes position angles of 116.°5,
125°, and 119°, respectively. Without independent
knowledge of the line of nodes position angle, there is no way to
choose between these models, and the case for an expanding circular
ring in NGC 4736 is weak. It is most likely that observed
rings are
elliptical or oval features rather than circular features, as shown by
statistics in section 9.3.
Fabry-Perot interferometry data and the slit spectroscopy of
van der Kruit (1976a).
Models of pure circular rotation, rotation plus
expansion, and a resonance dispersion orbit fit the data equally well
with required line of nodes position angles of 116.°5,
125°, and 119°, respectively. Without independent
knowledge of the line of nodes position angle, there is no way to
choose between these models, and the case for an expanding circular
ring in NGC 4736 is weak. It is most likely that observed
rings are
elliptical or oval features rather than circular features, as shown by
statistics in section 9.3.
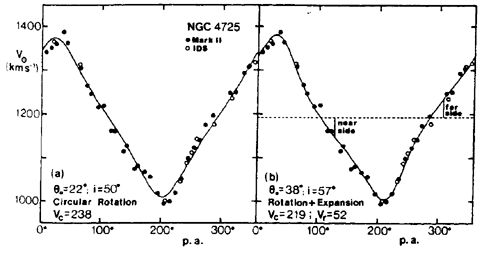
The best published cases of inner rings showing clear asymmetries (rather than just apparent line of nodes shifts) in the velocity-position angle diagram are NGC 1433 (Buta 1986b) and NGC 4725 (Buta 1984, 1988; Wevers et al. 1984). This is shown for NGC 4725 in Figure 55. In the case of NGC 1433, the asymmetry is readily explained in terms of the elliptical shape of the inner ring. In spite of the low inclination of this galaxy, the deviations from circular motion are obvious in the velocity-position angle diagram and can be fitted by a rotating elliptical ring where the radial and tangential velocity components in the rotating frame vary sinusoidally with position angle in the galaxy plane. However, NGC 4725, being more inclined and suffering interaction with a nearby companion, does not have sufficiently well-determined orientation parameters to yield a unique interpretation. The velocity-position angle diagram can be fit either by rotation plus uniform expansion (see right panel in Figure 55), or a precessing ellipse (see Buta 1988). In the expanding ring interpretation, the expansion velocity derived was 52 ± 7 km s-1 from optical interferometry and 40 ± 13 km s-1 from HI observations. However, no matter how well this kind of model may fit the data, it is unlikely that a large ring crossed by a bar is due to some kind of nuclear explosion (see Sanders and Bania 1976).
|
Although the inner rings of NGC 1433 and 4725 display clear asymmetries in their velocity-position angle diagrams, the lack of asymmetry does not mean that there are no noncircular motions present. If an oval ring presents an aspect such that the observer is viewing the ring down its intrinsic major or minor axis, then the motion along the ring at the projected galaxy minor axis will be purely tangential, and no asymmetry will be seen in the velocity-position angle diagram. Two examples where this may be the case are the inner rings of NGC 3351 and 4736 (Buta 1988).
Lindblad Precession Frequencies
Rotation curves derived for ringed or nonringed galaxies have been used
to infer resonance locations by deriving the so-called Lindblad
precession frequencies,  ±
±  / 2,
where
/ 2,
where  is the
circular angular velocity and
is the
circular angular velocity and  is the radial epicyclic
frequency. We describe in this section a sampling of studies where
these frequencies have been derived. In the linear theory, the location
of the inner Lindblad resonance is where the pattern speed equals
is the radial epicyclic
frequency. We describe in this section a sampling of studies where
these frequencies have been derived. In the linear theory, the location
of the inner Lindblad resonance is where the pattern speed equals
 -
-  / 2 and the location of the
outer Lindblad resonance is
where the pattern speed equals
/ 2 and the location of the
outer Lindblad resonance is
where the pattern speed equals  +
+  / 2. Corotation is where
the pattern speed equals the circular angular velocity in the disk.
Since
/ 2. Corotation is where
the pattern speed equals the circular angular velocity in the disk.
Since  is derived from
the radial derivative of the rotation
curve, a smooth curve is often fitted to rotation curve points to
reduce noise. These studies have usually not allowed for the effects of
velocity dispersion on the observed rotation curve, especially in the
inner regions, and treat the resonances as narrow in radius.
Contopoulos (see discussion in
Pfenniger 1996)
discusses the nonlinear
situation. Multiple-ringed galaxies are often the best choices for such
analyses, because one can check for consistency between the locations
of the rings and a single pattern speed.
is derived from
the radial derivative of the rotation
curve, a smooth curve is often fitted to rotation curve points to
reduce noise. These studies have usually not allowed for the effects of
velocity dispersion on the observed rotation curve, especially in the
inner regions, and treat the resonances as narrow in radius.
Contopoulos (see discussion in
Pfenniger 1996)
discusses the nonlinear
situation. Multiple-ringed galaxies are often the best choices for such
analyses, because one can check for consistency between the locations
of the rings and a single pattern speed.
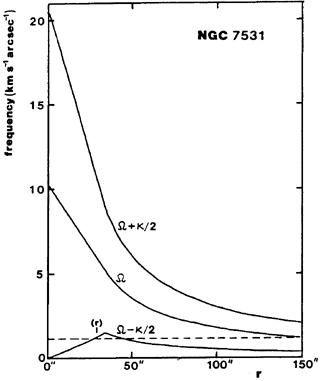
Buta (1987a)
estimated the precession frequencies in the single-ringed galaxy NGC 7531 (see Figure 56),
based on an
analytic function fitted to the observed rotation curve. In this case the peak
of  -
-  / 2 lies slightly outside the
mean deprojected radius
of the inner ring, but in any case the ring is located very close to
the maximum of this function. The horizontal line in
Figure 56 assumes the inner ring is located at
ILR, which places corotation in the region of the faint outer arms.
/ 2 lies slightly outside the
mean deprojected radius
of the inner ring, but in any case the ring is located very close to
the maximum of this function. The horizontal line in
Figure 56 assumes the inner ring is located at
ILR, which places corotation in the region of the faint outer arms.
|
Telesco & Decher (1988) derived the precession frequencies for the well-known Seyfert 2 galaxy NGC 1068. Using a rotation curve based on a combination of stellar absorption line velocities over the region of the bright nuclear pseudoring, and gaseous emission line velocities outside this region, they deduce that for a pattern speed of 50 km s-1 kpc-1, the pseudoring of IR luminous star formation, brightest CO features, and the brightest non-nuclear HII regions lies between two ILR's. In their interpretation, the ends of the nuclear bar lie just inside the inner ILR of the system. They conclude that the luminous burst of star formation in the inner regions of NGC 1068 is due mainly to bar-driven gas flow and indirectly to the Seyfert activity in the nucleus. Their rotation curve did not extend far enough to deduce whether the location of the outer ring of NGC 1068 is consistent with the location of OLR for the same pattern speed.
Arsenault et al. (1988)
derived a detailed rotation curve for M100
using a Fabry-Perot velocity field. By assuming that corotation lies at
the ends of the weak primary bar, they deduced from the
 -
-  / 2 curve that the nuclear
pseudoring lies between the
two ILR's of a double ILR. As we have already discussed in
section 9.7, more recent and more detailed
studies support this idea. This galaxy has no other rings.
/ 2 curve that the nuclear
pseudoring lies between the
two ILR's of a double ILR. As we have already discussed in
section 9.7, more recent and more detailed
studies support this idea. This galaxy has no other rings.
Schommer et al. (1988) derived precession frequency curves for the barred Seyfert 2 galaxy NGC 5728. In this case, by assuming the bar ends at CR, they deduced that the nuclear ring of the galaxy is located just inside an ILR.
Devereux et al. (1992) used a combined optical/CO rotation curve to evaluate precession frequencies in the SB(r)b spiral NGC 3351. In order to connect the location of the bright nuclear ring to the region of the ILR's, the pattern speed was such that corotation was placed at 1.2 times the bar radius. This also placed the inner ring inside corotation.
From a combined high resolution CO and optical rotation, Kenney et al. (1993) deduced the precession frequencies in the (R'1)SAB(rs)ab spiral NGC 3504. In this case, by assuming corotation lies at the ends of the bar, they deduced that the partial nuclear ring and inner starburst in this galaxy lies between two possible ILR's and that the pattern speed is also consistent with the outer pseudoring being located near the outer Lindblad resonance.
Finally, Ryder et
al. (1996)
have used an HI rotation curve to deduce
resonance locations in NGC 1433. Ryder et al. found reasonable
consistency with a single pattern speed for the locations of
the outer and inner pseudorings of this galaxy, with the outer
pseudoring being located near the OLR and the inner pseudoring
being located near the inner 4/1 resonance, where  p =
p =
 -
-  / 4. The
resolution of the HI rotation curve was
not high enough to deduce whether the nuclear ring of this
galaxy is connected to the region of the ILR's.
/ 4. The
resolution of the HI rotation curve was
not high enough to deduce whether the nuclear ring of this
galaxy is connected to the region of the ILR's.
Complex Motions in Nuclear Ring Regions
The regions of nuclear rings in galaxies sometimes show complex velocities with large velocity dispersions, noncircular motions, and even multiple components. Virtually every example studied is characterized by rapid rotation, noncircular motions, and sometimes high velocity dispersion compared to HII regions away from the nuclear region. A representative case is NGC 5728, a Seyfert 2 galaxy studied by Schommer et al. (1988), who mapped the velocity field of the nuclear ring with a Fabry-Perot interferometer. The emission map from this study revealed a bright nucleus and a bright arc or partial ring of emission. Strong noncircular motions were detected in a velocity cut along the kinematic major axis. Rapid rotation characterizes the region, and double-peaked line profiles were detected in the nucleus. The latter may be connected to the Seyfert activity, and not all nuclear rings include such an active nucleus.
Particularly interesting in this regard has been the detection of a nuclear gas ring in the Seyfert 1 galaxy NGC 4151, by Vila-Vilaró et al. (1995). In this case, the ring appears red in color index maps owing to dust extinction. Gas motions in the ring were measured by Robinson et al. (1994), who detected a significant increase in the velocity dispersion in this region. Vila-Vilaró et al. suggest that the reddened arcs in the nuclear ring of NGC 4151 are regions where gas from the leading regions of the bar encounter gas on the x2 family of periodic orbits. This is very much like the origin of ``twin peaks'' CO emission from other barred galaxies (section 9.7 ). In addition, these authors identified a close alignment of the extended narrow line region with the nuclear gas ring, and suggest that the collimation of the AGN ionizing radiation field and the gas flows due to the bar potential are closely related. In the Seyfert 1.5 barred spiral galaxy NGC 1365, the [OIII] emission lines reveal two components in the central regions: one component representing the circumnuclear ring in rotation, the other component the bipolar outflow of hot gas from the nucleus, forming a cone aligned along the minor axis (Hjelm & Lindblad 1996, Lindblad et al. 1996), also roughly aligned with the nuclear ring.
This completes the main observational discussion. We now turn to the theoretical parts of this review.