


13.2. Self-gravitating Rings and Nuclear Spirals
When more self-gravity is introduced in the gas component, the nuclear
rings formed at ILR are much more unstable, and short-lived. This has
already been shown in simulations of gas flow in a bar potential, when
self-gravity of the gas is taken into account
(Fukunaga & Tosa 1991;
Wada & Habe 1992;
see also Elmegreen
1994a).
In the presence of an
ILR, the gas accumulates in a ring towards the center, but the local
instabilities it undergoes there make the ring fragment into clumps; the
ring is also more elongated, and more asymmetric. Two big clumps
gather at the end of the elongated ring, and re-inforce the bar
potential. This produces more gravity torques, and a rapid loss of
angular momentum for the gas in the ring. The ring collapses towards
the center in a few rotations.
However, the results of these simulations are highly dependent on the
fact that the stellar potential remains fixed and barred, with an
imposed pattern speed. In fact the gas infall, when sufficiently
massive, will perturb significantly the potential in the center, the
pattern speed of the bar, and even can destroy the bar
(Friedli & Benz 1993).
A more likely behavior is the formation of two ILR's, due
to the high mass concentration, the formation of a phase-shifted bar,
due to the existence of perpendicular x2 orbits
(Shaw et al. 1993;
Combes 1994),
or the formation of a secondary bar inside the primary
one (see section 16). Both behaviors
represent mechanisms to fuel the
gas towards the nucleus, and extend towards the center the effects of
the gravity torques from the primary bar. The actual behavior depends
however on the gas simulation code and on its assumed viscosity.
With the help of self-consistent simulations with stars and fluid-gas
(through the beam-scheme hydrodynamical code, e.g.,
Sanders & Prendergast
1974),
Junqueira & Combes
(1996)
have shown that a large
mass concentration due to gas infall can both destroy the bar and help
an m = 1 instability to grow. The latter phenomenon is quite stable,
and prevents at the same time further gas infall.
Many galaxies are observed with their nuclei off-centered with respect
to neighboring isophotes, and lopsided morphologies have been known
for a long time
(Baldwin et al. 1980).
Asymmetric features are
preferentially observed in the distribution of gas in late-type spiral
galaxies. In a sample of 1700 galaxies,
Richter & Sancisi
(1994)
have found that more then 50% of HI distributions are significantly
asymmetrical. Stellar disks reveal also lopsidedness, in about 30% of
cases, in the old population traced by the K-band (2.2µ,
Rix & Zaritsky 1995).
In several cases these features can be identified as
one-armed spirals (m = 1 mode, e.g.,
Phookun et al. 1992,
1993).
More frequently, nuclei of galaxies are observed displaced with respect to
the gravity center, as in M33, M101 or M31
(Bacon et al. 1994).
Our own galaxy appears to experience such an off-centering, at
least as far as
the gas disk is concerned: about three quarters of the molecular mass
of the nuclear disk is at positive longitude, and one quarter at
negative longitude (e.g.,
Bally et al. 1988).
Asymmetries are
also seen at larger scale in atomic gas, while much of the neutral gas
between a
few hundred parcsecs and 2 kiloparsecs from the nucleus lies in a
tilted disk whose plane of symmetry is inclined by 20° with
respect to the galactic plane (e.g.,
Burton 1992).
Barred spiral galaxies can have their kinematical center displaced from the bar
center
(de Vaucouleurs &
Freeman 1973;
Marcelin &
Athanassoula 1982;
Phookun et al. 1992;
Odewahn 1996).
It has been suggested by
Colin & Athanassoula
(1989)
that offset bars can generate a one-armed structure in the disk.
The frequency of asymmetries and lopsidedness in spiral galaxies
requires some efficient dynamical mechanism to generate and maintain
them. The swing amplifier can play a role, but the dominant amplified
mode depends essentially on the degree of self-gravity of the disk
(e.g.,
Jog 1992):
high disk-to-halo mass ratio, low velocity dispersion,
and high gas fraction are favorable. One can remark also that a direct
m = 1 mode is favored by the absence of damping at resonances, since
there is no ILR possible ( -
-  < 0).
Another mechanism can
be the excitation of a leading m = 1 spiral by a retrograde companion
(Thomasson et
al. 1989).
In that case, elongated orbits excited by the
tide precess at a rapid and retrograde rate, and form a leading
retrograde spiral. This occurs with a close interaction, when the disk
of the target is embedded in a very massive halo. Since galaxies with
leading arms are very rare, this might mean that the halo-to-disk mass
within the visible disk is lower than unity for most spiral galaxies.
It is a general observation that spiral galaxies with m = 1 structures
display also higher order m = 2, 3, ... structures, and the sense
of arms winding is usually the same for each set of structures. An interesting
exception is NGC 4622, which we discuss specially in
section 17.1. One of
the results of the N-body simulations by
Zang and Hohl (1978)
is that the
introduction of a significant fraction of counter-rotating stars can
produce one-armed structures, in addition to the m = 2 instability. The
m = 1 instability has been confirmed analytically by
Palmer & Papaloizou
(1990)
in the case of equal numbers of direct and retrograde
stars. However, one-armed spirals do not possess a larger fraction of
stars in counterrotation than galaxies with two arms. Another
possibility to trigger asymmetries and lopsidedness is infall of gas
(Sancisi et al. 1990;
Phookun et al.
1993).
< 0).
Another mechanism can
be the excitation of a leading m = 1 spiral by a retrograde companion
(Thomasson et
al. 1989).
In that case, elongated orbits excited by the
tide precess at a rapid and retrograde rate, and form a leading
retrograde spiral. This occurs with a close interaction, when the disk
of the target is embedded in a very massive halo. Since galaxies with
leading arms are very rare, this might mean that the halo-to-disk mass
within the visible disk is lower than unity for most spiral galaxies.
It is a general observation that spiral galaxies with m = 1 structures
display also higher order m = 2, 3, ... structures, and the sense
of arms winding is usually the same for each set of structures. An interesting
exception is NGC 4622, which we discuss specially in
section 17.1. One of
the results of the N-body simulations by
Zang and Hohl (1978)
is that the
introduction of a significant fraction of counter-rotating stars can
produce one-armed structures, in addition to the m = 2 instability. The
m = 1 instability has been confirmed analytically by
Palmer & Papaloizou
(1990)
in the case of equal numbers of direct and retrograde
stars. However, one-armed spirals do not possess a larger fraction of
stars in counterrotation than galaxies with two arms. Another
possibility to trigger asymmetries and lopsidedness is infall of gas
(Sancisi et al. 1990;
Phookun et al.
1993).
Miller & Smith (1992)
have studied, through N-body simulations of
disk galaxies, a peculiar oscillatory motion of the nucleus with respect
to the rest of the axisymmetric galaxy. They interpret the phenomenon
as a local instability, or overstability, of the center, but not in terms
of a normal mode. Their models did not include any gas component.
The presence of gas may change the picture considerably.
A qualitatively different mechanism has been studied in the context of
massive gaseous disks around young stellar objects, i.e. nearly
Keplerian disks, by
Adams et al. (1989).
They discovered numerically a
family of unstable normal modes where the star did not lie at
the center of mass of the system. The m = 1 instability arises
essentially from the displacement of the central star from the center
of mass of the system, which creates an effective forcing potential.
Shu et al. (1990)
presented an analytical description of a modal
mechanism, the SLING amplification, or ``Stimulation by the Long-range
Interaction of Newtonian Gravity''. This mechanism uses the corotation
amplifier, where the birth of positive energy waves outside strengthens
negative energy waves inside. In the SLING mechanism, a feedback cycle
is provided by four waves outside corotation; long-trailing waves
propagate from the OLR inward to the Q-barrier at CR where they refract
in short trailing waves. These propagate outwards, cross the OLR, and
reflect back to the outer edge of the disk. This is a critical point:
the whole amplification mechanism depends on the reflecting character
of this outer edge (cf.
Noh et al. 1992).
Then a short leading wave
propagates inwards from the edge, through OLR, towards CR, where it
refracts again into a long leading wave, which is then reflected at
OLR. An essential point here is also the ability of waves not to be
absorbed at OLR, which is why this mechanism applies to gaseous disks
only. Using a WKBJ analysis, they derived from the dispersion
relation, and the condition of a constructive reflection, the required
pattern speed for these modes.
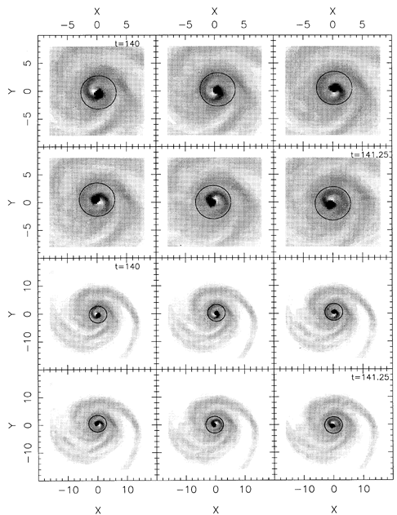
Figure 80. Development of a central
m = 1 wave in the gas component, rotating at  p = 400 km
s-1 kpc-1. The circle, at
3 kpc, indicates the OLR; from
Junqueira & Combes
(1996).
p = 400 km
s-1 kpc-1. The circle, at
3 kpc, indicates the OLR; from
Junqueira & Combes
(1996).
|
The same mechanism could be applied to massive gaseous disks
in the central parts of galaxies possessing high central
mass concentrations, as proposed by
Junqueira & Combes
(1996).
At first, a bar instability accumulates gas towards the center, when
it becomes unstable and forms an m = 1 spiral mode
(Figure 80).
The mode grows in a dynamical time, and remains quasi-steady until
the end of simulations (during 2 x 109 yrs). The gaseous disk mass
represents more than 25% of the central mass. In the density
plots, the spiral is conspicuous until 3 kpc radius, and other more transient
features, with much lower angular speeds, dominate at larger
radii. The Fourier analysis of the total potential indicates a very
high pattern speed of  p = 400km s-1 kpc-1
for the
central m = 1 spiral, which corresponds to the OLR at 3 kpc
(Figure 81). This pattern speed is much higher
than the speed
at larger radii; there is no coupling between several modes, as was
suggested for bars within bars. In the latter case, the corotation of
the small bar is the inner resonance of the large one, and there exists
a non-linear interaction between the two patterns
(Tagger et al. 1987).
A non-linear interaction between two modes with azimuthal mode
numbers m = n and m = n + 1 was proposed by
Laughlin & Korchagin
(1996)
to trigger m = 1 instabilities in low-mass disks, and was confirmed
through self-consistent hydrodynamic simulations.
p = 400km s-1 kpc-1
for the
central m = 1 spiral, which corresponds to the OLR at 3 kpc
(Figure 81). This pattern speed is much higher
than the speed
at larger radii; there is no coupling between several modes, as was
suggested for bars within bars. In the latter case, the corotation of
the small bar is the inner resonance of the large one, and there exists
a non-linear interaction between the two patterns
(Tagger et al. 1987).
A non-linear interaction between two modes with azimuthal mode
numbers m = n and m = n + 1 was proposed by
Laughlin & Korchagin
(1996)
to trigger m = 1 instabilities in low-mass disks, and was confirmed
through self-consistent hydrodynamic simulations.
Figure 81. Power spectrum analysis for the
gas density of Figure 80 and for the
corresponding total potential. The
identified perturbation extends up to the outer parts of the disk.
| m = 1 (potential)
|

|
| r
|
| m = 1 (gas)
|

|
| r
|
The power spectrum analysis for the gas density of
Figure 80
and the corresponding total potential reveals that the influence of the
fast-rotating m = 1 pattern extends towards the edge
(Figure 81). This can be explained for the
potential, since
the m = 1 perturbation is a periodic move of the center of mass,
and is instantaneously felt in the whole disk, but the signature in the gas
density is more remarkable. The stellar component does not follow the
m = 1 spiral with as much contrast, but the off-centering of its center
of mass is also conspicuous. The two components oscillate in phase
opposition, while the massive dark halo, represented by an analytical
Plummer component, is nailed down to the center. The large gaseous
condensations in the center of spiral galaxies can therefore give rise
to new instabilities, and account for some of the observed off-centered
nuclei or lopsided distributions.



 -
-  < 0).
Another mechanism can
be the excitation of a leading m = 1 spiral by a retrograde companion
(Thomasson et
al. 1989).
In that case, elongated orbits excited by the
tide precess at a rapid and retrograde rate, and form a leading
retrograde spiral. This occurs with a close interaction, when the disk
of the target is embedded in a very massive halo. Since galaxies with
leading arms are very rare, this might mean that the halo-to-disk mass
within the visible disk is lower than unity for most spiral galaxies.
It is a general observation that spiral galaxies with m = 1 structures
display also higher order m = 2, 3, ... structures, and the sense
of arms winding is usually the same for each set of structures. An interesting
exception is NGC 4622, which we discuss specially in
section 17.1. One of
the results of the N-body simulations by
Zang and Hohl (1978)
is that the
introduction of a significant fraction of counter-rotating stars can
produce one-armed structures, in addition to the m = 2 instability. The
m = 1 instability has been confirmed analytically by
Palmer & Papaloizou
(1990)
in the case of equal numbers of direct and retrograde
stars. However, one-armed spirals do not possess a larger fraction of
stars in counterrotation than galaxies with two arms. Another
possibility to trigger asymmetries and lopsidedness is infall of gas
(Sancisi et al. 1990;
Phookun et al.
1993).
< 0).
Another mechanism can
be the excitation of a leading m = 1 spiral by a retrograde companion
(Thomasson et
al. 1989).
In that case, elongated orbits excited by the
tide precess at a rapid and retrograde rate, and form a leading
retrograde spiral. This occurs with a close interaction, when the disk
of the target is embedded in a very massive halo. Since galaxies with
leading arms are very rare, this might mean that the halo-to-disk mass
within the visible disk is lower than unity for most spiral galaxies.
It is a general observation that spiral galaxies with m = 1 structures
display also higher order m = 2, 3, ... structures, and the sense
of arms winding is usually the same for each set of structures. An interesting
exception is NGC 4622, which we discuss specially in
section 17.1. One of
the results of the N-body simulations by
Zang and Hohl (1978)
is that the
introduction of a significant fraction of counter-rotating stars can
produce one-armed structures, in addition to the m = 2 instability. The
m = 1 instability has been confirmed analytically by
Palmer & Papaloizou
(1990)
in the case of equal numbers of direct and retrograde
stars. However, one-armed spirals do not possess a larger fraction of
stars in counterrotation than galaxies with two arms. Another
possibility to trigger asymmetries and lopsidedness is infall of gas
(Sancisi et al. 1990;
Phookun et al.
1993).





